2024年度数学史講義資料3:Hilbert 不変式論史(新説編)

ver.2024.12.20 14:16-進行中の研究をもとにしているため、内容を変更する可能性があります。

この講義資料3では、講義資料2の最後で説明した、定説の矛盾を受けて発見した「忘れられた証明」をキーにして、林が、この数カ月でその大まかな骨組みを建設した「Hilbert 不変式論の新説」を紹介する。この資料3の内容は、主には数学的で、その多くは、[Hilbert1888][Hilbert1889a][Hilbert1889b][Hilbert1889c][Hilbert1890]の内容の新説の立場からの史料分析になる。しかし、有限基底定理のルーツの推測などの、歴史学で「解釈」 "interpretation" と呼ばれる事も行う(2.4と2.5)。 そして、次の講義資料4で、神学事件で何が起きたのかを数学者間の間の書簡の翻刻・分析から読み解くことになる。

講義資料2で示した、この講義資料3の内容の「目次」を、ここに reproduce しておく。

• 1. 二つの論文[Hilbert1889a][Hilbert1890]の数学的内容の解説。
• 2. 林の新説に基づく 1890年までの Hilbert 不変式論史。
• 2.1. 1888年3月 Leipzig: Gordan 定理二つの別証明。
• 2.2. 三つの速報: [Hilbert1888],[Hilbert1889b,c]。
• 2.3. 忘れられた証明: [Hilbert1889c]。
• 2.4. 整数版有限基底定理のルーツは?
• 2.5. 有限基底定理の二つの証明についての謎と、それへの暫定的解答。
• 2.6. 今後の課題。

1. 二つの論文: [Hilbert1889a][Hilbert1890]

論文などの出版が大幅に電子化・ネット化している現代、数学の世界での成果の公表がどうなっているのか寡聞にして知らないが、少なくとも林が数学を専門でやっていたころまでは、学士院紀要などの速報を掲載するメディアに証明などは省略したり、概要だけを書いた速報を投稿し、その後、専門誌に完全な論文、フル・ペーパーを投稿するということが行われていた。そして、証明が大切な数学では、専門誌に掲載されたフル・ペーパーが非常に重要視されていたと記憶している。そのためフル・ペーパーが出ているのに、わざわざ速報を読むということは、滅多になかったように思う。

おそらくは、今もそうだろうし、少なくとも Hilbert の時代は、そうだった。そのため、多くの数学者にとって、Mathematische Annalen の様な専門誌に掲載された論文で、Hilbert の不変式論を理解していたはずだ。そういう観点からすると、Hilbert の不変式論とは、[Hilbert1889a][Hilbert1890][Hilbert1893]のことだと見えたはずである。これは三つとも Cayley の予想についてのもので、そして、今でも、Hilbert の Classical Invariant Theory とは、この三つのことだとして、その内容が教科書やモノグラフで紹介される。

1. 1890年までの Hilbert 不変式論：論文[Hilbert1889a]と[Hilbert1890]の内容

この講義では、時間の関係で、零点定理が登場し、後の1980年代に Geometric Invariant Theory と呼ばれる分野の元となった[Hilbert1893]には、ほとんど触れることができず、1890年までにフォーカスをあてている。つまり、この講義での「外から見た Hilbert 不変式論」とは、[Hilber1889a][Hilbert1890]のことになる。そこで、まずは、歴史を無視して、現代の教科書などにも書かれている、この二論文の内容のダイジェストを解説することにしよう。

この1と、次の2で取り上げる二つの論文と三つの速報を執筆時期順に並べると次の様になる。

一番古い[Hilbert1889a]が、Hilbert が Leipzig で Gordan に会った際に着想し、その後、Göttingen に Klein を尋ねた時に、その原稿を手渡したらしい、あの論文である。では、その内容を解説しよう。

1.1. Gordan 定理の別証明[Hilber1889a]の内容

Hilbert が herrlich kurze und pointirte と書いた様に、[Hilber1889a]は非常に短い証明であった。こちらが、その論文を GDZ でPDF形式でダウンロードしたものだが、3ページ強しかない。その短さの理由の一つは、すでに述べた様に、既存の結果を上手に組み合わせた証明だったことがある。 そして、実は短かった理由はもう一つあって、証明や記法が、現代の基準からすると、非常にいい加減だったからである。

この証明の最大のポイントは、binary な不変式を表現する方法として、良く知られていた「根の差」を使う点であった。この「根の差」の考え方を簡単に説明しよう。 \(m\)次\(n\)変数の form \(f(x_1,\ldots,x_{n-1},x_n)\) の変数の一つ、例えば最後の変数に1を代入して \(f(x_1,\ldots,x_{n-1},1)\) を作ると、これはもう form にはならず、変数が一つ少ない多項式になる。それを \(p(x_1,\ldots,x_{n-1})\) とすると、\(f\) の斉次性より、 \[ f=x_n^m\cdot p\left(\frac{x_1}{x_n},\ldots,\frac{x_{n-1}}{x_n}\right) \] となる事がわかる。例えば、\(f(x_1,x_2)=x_1x_2+x_2^2\) とすると、\(p(x_1)=x_1+1\) なので、次の様になる。 \[ x_1x_2+x_2^2=x_2^2\left(\frac{x_1}{x_2}+1\right) \]

射影幾何学を学んだ人は、これは、\(n\)次元空間内の点の関数である \(f(x_1,\ldots,x_n)\) を、その斉次性を利用して、\((x_1,\ldots,x_n)\) を、\(n-1\)次元射影空間の斉次座標とみなすことにより、\(n-1\)次元射影空間上の関数 \(p(x_1,\ldots,x_{n-1})\) で表現しているのだと分かるだろう。

この対応は、binary の場合に非常に重要な帰結をもたらす。\(p\) が1変数多項式になるので、代数学の基本定理により一次式に因数分解できるからだ。 たとえば、\(f=a_0x_1^2+2a_1x_1x_2+a_2x_2^2\) に対応する多項式 \(p=a_0x_1^2+2a_1x_1+a_2\) が \[ p=a_0(x_1-\omega_1)(x_1-\omega_2) \] となったとすると、 \[ f=x_2^2a_0\left(\frac{x_1}{x_2}-\omega_1\right)\left(\frac{x_1}{x_2}-\omega_2\right)=a_0(x_1-\omega_1x_2)(x_1-\omega_2x_2) \] となる。

この時、判別式の一般的定義から、\(p\) の判別式を構成し、 それに根と係数の関係 \(\omega_1+\omega_2=-2a_1/a_0, \omega_1\omega_2=a_2/a_0\) を適用すれば、次の様になる事がわかる。 \[ a_0^2(\omega_1-\omega_2)^2=a_0^2((\omega_1+\omega_2)^2-4\omega_1\omega_2)=4(a_1^2-a_0a_2) \] つまり、Boole が発見した最初の不変式 \(a_0a_2-a_1^2\) は ground form に対応する多項式 \(p\) の判別式だったのである。

binary な ground form に上の様にして1変数多項式を対応させ、その根を \(\omega_1,\ldots,\omega_n\) だとする。その内の二つの根 \(\omega_i,\omega_j\) の差 \(\omega_i-\omega_j\) を \((i,j)\) と書くことにする。 そして、これらを変数の様に思い、その斉次式を考える。たとえば、上の例だと \(a_0^2(1,2)^2\) という「単項式」である。その様な根の式が、次の2条件を満たすとき、それは ground form の不変式となり、また、逆に、すべての不変式は、その様に書けることが知られている。

1. 根の対象式である。
2. \((i,j)\) の斉次式としてみた時、その各項に現れる根の出現の数は等しい。

この定理は、教科書などに書かれている既知の事実だったが、Hilbert は、こういう根の差の斉次式の各根の差 \((i,j)\) の指数を \((1,2)^{e^{1,2}}(1,3)^{e^{1,3}}\ldots(2,3)^{e^{2,3}}+\ldots\) の様に \(e^{i,j}\) と書く時、上の条件が \(e^{i,j}\) の整数係数の連立線形方程式で表されることに気が付いたのである([Hilbert1993],pp.118-119)。

そういう方程式に対しては、次の様な定理が成り立つことを、Gordan が[Gordan1873]で証明していた。また、これは彼の不変式論講義の第一巻[Gordan1885]でも解説されていた。これは Gordan の補題と呼ばれている。

つまり、整数係数線形連立方程式の非負整数解の集合には有限な基があるという定理である。 Hilbert は、\(e^{i,j}\) の方程式に、この補題を適用して、Gordan の補題が存在を保証する有限個の特殊解の線形結合を \((i,j)\) の指数として使うことにより、不変式になる根の差の斉次式の一般形を求めた([Hilbert1993],pp.118-119)。

しかし、まだ、これだけでは、条件1,2を満たす根の差 \((i,j)\) の斉次式の有限個の基は作れていない。\((i,j)^{e^{i,j}}\) の \(e^{i,j}\) の特殊解の線形結合には、非負整数係数 \(p_i\) があるからだ。たとえば、Gordan の補題が存在を保証する有限個の基の線形結合で、\(e^{i,j}\) 表現したとき、その基の数が \(m\) だとして、一般解を表す線形結合にはパラメータが \(m\) 個あるので、それを \(p_1,\ldots,p_m\) とすると、 特に、\(e^{1,2}\) に対しては、\(e^{1,2}=p_1d_1+\cdots +p_md_m\) となっているとする。

そうすると、 \[ (1,2)^{e^{1,2}}=((1,2)^{d_1})^{p_1}\cdots((1,2)^{d_m})^{p_m} \] となる。この \(p_i\) を何とかすればよいのだが、そのために Hilbert は次の様な補題を証明して使った。

この Hilbert の補題の証明と、これを使って、どうやって Gordan 定理を証明するかの詳細は、ここまで説明すれば、凡そ推測できるものと思うので省略する。Hilbert の補題の完全な証明は[Hilbert1993]のpp.116-117に、Gordan の補題と Hilbert の補題による Gordan 定理の別証明の詳しい話は、[Hilbert1993]のpp.118-120にあるで、関心があれば参照して欲しい。

先に、[Hilbert1889a]が短かったひとつの理由は、書き方や証明がいい加減だったからだとリマークしたが、例えば、この論文では Hilbert の補題には全く証明が与えられていない。証明の仕方のヒントさえ書いていない。それは基本対称式と power sum と、1変数代数方程式の根と係数の関係を使う短く初等的なものではあるが、それでも[Hilbert1993]では、三分の一ページほどを消費している。

Hilbert の補題のオリジナルは、次の様に書かれている。

Hilbert の不変式論講義[Hilbert1993]でも、この根の差を利用する別証明の話では、こういう省略が多い(特にp.99の最後のTheoremからp.101にかけて)。これを[Kung&Rota1984]の様に現代的厳密性と明瞭性のもとに書き直すと、かなり長くなる。おそらくは、月曜日の講義で transform transformation という言葉の19世紀と現代での理解の仕方の違いで示した様に、19世紀の人たちの思考パターンが、我々のものとは大きく違っていて、我々からは理解しにくいものも、案外簡単に理解できていたためではないのかとも思う。

講義資料1で行った transform, transformation という言葉の19世紀的使い方と現代的使い方の違いについて史料に基づいての議論と同じようなことを、これについても、行う必要があるのではないかと思うが、こちらはかなり難しい作業になるだろう。これからの数学史の課題として、ここではこれ以上議論しないことにする。最後に、そういう19世紀的思考法と我々の思考法の違いを二つリマークして、[Hilbert1889a]の解説を終わる。

リマークの一つ目は、Hilbert の補題で、Hilbert は、\(\omega_i\) を Grössen quantities 量と呼んでいる点である。あまりに一般的な言葉が使われいて、最初に読んだときに、正直戸惑った。Riemann が有名な講演「幾何学の基礎をなす仮説」で、多様体を構成するものを説明するとき、多様体を連続多様と離散多様体に分類し、前者を構成するものは、Punkt 点と呼ばれ、後者を構成するものは、Element 要素と呼ばれるとした。そして、それらの総合的な呼び名としては、Hilbert が使ったものと同じ Grösse 量という言葉を使っている。また、Kronecker の代数理論、あるいは代数的整数論と代数幾何学の融合理論も、algebrishe Grössen, algebraic qunatities の理論と名付けられていた。

当時のドイツでは、数学は Grösse の学問だと考えられていたというのは、20世紀が終わろうとするころに、数学者の集合論史観と現代数学史観を劇的に変えてしまったと言えるスペインの歴史家 José Ferreirós の歴史観の主要な論点の一つである[Ferreirós2008]。つまり、言い換えれば、Grösse というと、「数学の対象」という位の意味になると思えば良いのではないかと思う。

おそらく、Hilbert は、自分の議論の一般性に気付き、\(\omega_i\) を何と呼ぶか迷い、この様な一般的過ぎる言葉を使ってしまったのではないかと思う。 しかし、今はもう数学は量の学問ではない。これを現代的に言い換えれば､\(\omega_i\) は「可換環の要素」とでも言うか、「これらを不定元とする多項式環で考える」と言えば良いのだろう。あるいは、これは私の考え過ぎで、こういう言い回しが19世紀には普通だったということかもしれないが。

もう一つのリマークは、数学的には、もっと本質的である。今までの議論で、ground form に対応する多項式の根を考えた。しかし、ground form の係数は変数、あるいは、不定元なのである。それの根をどうやって考えられるのだろうか？19世紀の人たちが、これをどう考えていたのか私には大変不思議で良く分からないのだが、現代的な処理の仕方はある。これも[Kung&Rota1984]によるもので、ground form の係数と変数\(x_1,x_2\)を不定元とする複素係数の多項式環と、根と\(x_1,x_2\)を不定元とする複素係数の多項式環の二つを考えて、前者から後者に係数と根の関係を使って準同型を作り、それが単射であることを代数学の基本定理を使って示すというものである。詳細は、[Kung&Rota1984]のセクション４、Covariants in Terms of the Roots を見て欲しい。

\(x_1,x_2\)が入っているのは、今まで紹介した Hilbert の場合と違い、covariant で考えているからである。また、根を不定元とすると書いたが、binary form の根を考えるときには、普通は Hilbert の様にはせず、homogenized root というものを使い、\(n\)次の binary form は、 \[ f(x_1,x_2)=(\mu_1x_1-\nu_1x2)\cdots(\mu_nx_1-\nu_1x_n) \] の様に因数分解、つまり、一次式の積に分解する。右辺の \(\mu_i,\nu_i\) が、ひとつひとつの homogenized root で、要するに1次元射影空間の点を表す斉次座標である。つまり、Hilbert が、常にいわゆる cannonical な斉次座標 \([\omega_i,1]\) で考えているのに対し、一般の斉次座標 \([\mu_i,\nu_i]=[\nu_i\omega_i,\nu_i]\) で考える。従って、根と変数の多項式環は、\(\mathbb{C}[\omega_1,\ldots,\omega_n,x_1,x_2]\) ではなく、次の様になる。 \[ \mathbb{C}[\mu_1,\nu_1\ldots,\mu_n,\nu_n,x_1,x_2] \]

homogenized root の話と、不変式論向けの射影空間の話は、[Olver1999]の Chapter 2 にあるので気になる人は見ると良いと思う。これで[Hilbert1889a]の話は終わりにして、次に論文[Hilbert1890]の内容の説明に移る。

1.2. 有限基底定理の誕生[Hilbert1890]

Hilbert は数多くの数学史上に残る業績をあげているが、その最初のものが、[Hilbert1890]と、そこで登場した有限基底定理である。講義資料2で強調したように、この業績についての言及は、数学者間の感情的対立を通して学界政治闘争にまで発展した1920年代の数学基礎論論争を通して、いささか「行き過ぎ」た所がある。しかしながら、これが20世紀の抽象代数学や代数幾何学などに向けて、大きなステップとなったことは間違いがない。「行き過ぎ」というのは、「数学の哲学の問題にし過ぎている」という意味であり、その数学的意義や価値に疑問を投げかけているのではない。

既に、シラバスを含めて、何度か強調している様に、この論文が不変式論の論文として書かれ、その中で有限基底定理や Szygy 定理の様な重要な一般代数の定理が現れた、という良くある説明は間違いである。この論文は、有限基底理定理 Theorem I を基礎とする、新しい一般代数の理論、そして、Theorem I の応用としての、Gordan 問題の解決を報告することを目的として書かれている。そして、何故か、それらからは全くと言って良いほど孤立した Theorem II というものが含まれていた。そういう論文だったのである。そして、Theorem II が含まれていたことを無視すると、その様に書かれた理由は、既に講義資料2の最後で指摘した様に、Klein の示唆によるものと思われる。 この論文の構造と内容を解説しつつ、この論文は不変式論の論文として書かれてはいないということを実証していこう。

まずは、構造から見よう、この論文の冒頭には、次の様に目次 Inhalt, contents(英) が掲げられている。

1. Die Endlichkeit der Formen in einem beliebigen Formensysteme.
2. Die Endlichkeit der Formen mit ganzzahligen Coefficienten.
3. Die Gleichungen zwischen den Formen beliebiger Formensysteme.
4. Die charakteristische Function eines Moduls.
5. Die Theorie der algebraischen Invarianten.

1. The finiteness of forms in an arbitrary system of forms.
2. The finiteness of forms with integer coefficients.
3. The equations between the forms of arbitrary systems of forms.
4. The characteristic function of a module.
5. The theory of algebraic invariants.

この英訳で解ると思うが、I から IV までは、すべて一般的 form についてのセクションあるいはチャプターなのである。そして、最後の V で初めて不変式 Invarianten invariants という言葉がでてくる。実際、I～IVまでには、この目次の V の Invarianten 意外は、不変式論に由来する言葉が全くない。それは論文のPDFをサーチしてみればすぐにわかる。つまり、これは Klein が Hilbert に勧めた様に書かれた、「不変式論の重要な問題の解決を応用として含む、一般代数としての form についての新理論」なのである。

1.2.1. セクションIの内容：体上の有限基底定理

セクションIが、この論文[Hilbert1890]の心臓部である。他は、セクションIIを例外として、皆、この定理 Theorem I の帰結として書かれている。そして、セクションIIだけは孤立している。しかし、実は、セクションIIこそが、全てのルーツであったことは、後に2.1で実証する。

この論文を現代の数学者が読むと、大きな違和感に捉われると思う。これは「異形の論文」である。何が異形かというと、論文の書き方である。異様な書き方は複数あるが、特に目立つのが、論文の始め方である。それは、先ほどの目次のすぐ下から次の様に始まる。

要約すると、

ある Rationalitätsbereich (domain of rationality) の数を係数とする無限個の form のシステムが与えられた時、その中の有限個の \(F_1,F_2,\ldots,F_m\) を選んで、システムの任意の form \(F\) を、同じ Rationalitätsbereich の form \(A_1,\ldots,A_m\) で、 \[ F=A_1F_1+\cdots +A_mF_m \] と表すことができるかということが問題となる。この問題に決着をつけるために、次の Theorem I を証明する：

この書き方が何故異様かというと、問題の背景の説明が一切無いからである。どうして、\(A_1F_1+\cdots +A_mF_m\) という形式を考えたのか、その背景説明がない。実は、背景はちゃんとあり、 Klein が19世紀数学史[Klein1926]で語ったように、Kroneckersche Ansätze mit Dedekindscher Denkweise, Kroneckerian approaches with Dedekindian thinking なのである。つまり、「Kronecker の Modul の理論を、Dedekind の System の方法で拡張するという問題を考える」と言えば良いのである。しかし、その Kronecker の Modul は、Theorem I についての長い議論が終わった後で、初めて言及される。

一方で、すでに解説した[Hilbert1889a]では、短い論文ながら、冒頭に Gordan がこういう定理を証明しているが、それの別証明を与えるのが論文の目的だと、Mertens という数学者の別証明にも触れながら丁寧に解説してある。それが普通の論文というものであろう。同じ時期に書かれていながら、この対照は、何故なのか良く分からない。その死後に、Hilbert が一方的に自分の「論敵」に仕立ててしまう Kronecker を前面に出したくなかったのだと考えることもできるだろう。しかし、結局は Kronecker の名を出し、Kronecker の論文を引用して、自らの研究との類似性まで書いているので、このちょっと意地悪な解釈は、おそらく的外れなのだろう。

先ほど、[Hilbert1889a]の Hilbert の補題で、添え字を全く省略してしまうという、現代では考えられないような書き方を見た。こういう省略した書き方、19世紀の不変式論では、結構、似たものが多いのである。つまり、[Hilbert1889a]は、講義資料1で紹介した19世紀の transform という言葉の使い方の様に、現代のそれとは大きく違う古いスタイルで書かれた論文だと言えるだろう。それを Hilbert は旅の途上で、二週間ほどの短期間で執筆して完成させている。Königsberg に返って書けば十分なのに、そうしたと言うことは、執筆に何の困難も感じなかったのだろう。

一方で、時間の都合で、今回の講義では見せないが、Hurwitz から Klein への書簡に、Hilbert が、この論文[Hilbert1890]の執筆に大きな困難を覚えていたことが書かれているものがある。ほぼ、同時に得られた二つの成果の執筆における、この違いは何なのだろうか。私は、ここに Hilbert が成し遂げた大きな飛躍を感じる。つまり、有限基底定理を、それまでの数学の上に連続的に置いて、その意味を説明したり、証明したりすることに困難を感じたのではないかと思うのである。

この論文には、このイントロの背景説明の問題の他にも、同じような問題が繰り返し現れる。それは、上に書いた様にパイオニアの宿命という側面もあっただろうが、Hilbert の叙述のスタイルの悪さの問題である様にも思う。実際に Hilbert の、この頃の論文を読むと、少し書き変えれば断然読み易くになるのにと思うことが良くある。また、どうやら、Klein も、Hilbert の論文の書き方には問題があると思っていた証拠が幾つか存在する。そして、それが、神学事件の一因だったのではないかと思う。この点においては、私は McLarty に共感する。Gordan も Hilbert の論文の書き方には大きな不満をもっていたはずだ。

さて、こういう問題は、史料を提示しながら、段々と証拠だてて行くことにして、セクションIの内容の解説に戻ろう。ここまで説明した様に、背景説明なしの問題設定というイントロとは言えないような短いイントロの後、論文は、Theorem I で始まる。その statement は、既に講義資料2で説明したが、それより[Hilbert1890]の書き方に近づけた形でのべると、次の様になる。

内容はもう良いだろうが、少し気になる用語だけ検討しておこう。講義資料2では、form の係数は適当な体から取るとした。しかし、実際の論文では、Hilbert は、ここでは講義資料1の話題1で紹介した Kronecker の用語 Rationalitätsbereich を使っている。そして、Hilbert は、これが何を意味しているのか、何の説明もしていない。

もし、これが講義資料1の話題1で説明したものと同じならば、実数体や複素数体が排除されてしまう。それでは、セクションVの不変式論への応用が出来ない。 実は、Kronecker が係数を整数に fix したのは、1882年の事で[Kronecker1882]、それまではどうやら曖昧だったらしい。そのため、例えば、1897年の Zahlbericht[Hilbert1897a] で、Hilbert が代数的整数論を論じたときには、Kronecker の1853年の古い論文を引用して Rationalitätsbereich を説明し、Dedkind などの Körper, Zahlkörper と同じだという様な説明をしている。ということで、Hilbert が想定しているのは、複素数体の部分体だという位にしておこう。実際、これがどの様な体を考えていたのかは、以下の議論には殆ど影響しない。セクションVで不変式論に応用しないといけないので、少なくとも複素数体が入っていれば、それで十分なのである。

定理のステイトメントの後は、証明のはずだが、ここで Hilbert は道草を始める。これが背景説明なしのイントロという問題の次の書き方の問題である。Theorem I の証明は、最終的には、変数の数についての数学的帰納法で行われることになるのだが、Hilbert は、最初、それを説明しない。

そして、変数の数が3までの場合に、定理を個別に証明する方法を議論し始めるのである。何故、その様な書き方をしたのか、実に不思議である。McLarty[MrLarty2012]は、証明が、その時代の人には目新しすぎたためだろうとしているが、Hurwitz は、Hilbert の証明は簡単だ、それをどうやって分かりにくく書けるのか不思議だとも Klein への書簡に書いている。

また、従来の見方からすると、[Gray2000]で、Gray が主張した様に、非構成的な代数の証明を前面に打ち出したことで、それまで Hilbert が意図的に謙虚に接していたために、良好だった Kroncker との関係が悪化しただろうと予想できる。ところが、実は現実は正反対であったようで、 Kronecker や、その弟子たちが、[Hilbert1890]の結果を、Berlin では良く知られたことに過ぎず、Kronecker の算術的代数学の不変式論への応用に過ぎないと思っていた可能性を示唆する史料も存在するのである。これは有限基底定理のルーツを考える2.4で見せる。

ということで、どうして、そういう個別の証明を考えようとしたのか、また、説明しようとしたのか、その動機はわからない。しかし、いずれにせよ、Hilbert が、どの様に論文を書いたかは説明しておきたいし、また、特に1変数の場合は、Theorem I の数学的帰納法による証明のベースケースになる。また、実は2変数の場合は、宿題を出すのに都合が良いので、この「個別証明」について、詳しく説明しておこう。

まず、変数の数が1、つまり、\(x\) だけが変数なのであれば、form とは、結局単項式 \(ax^n\) のことである。そうすると、form の列は、 \[ a_1x^{n_1},\, a_2x^{n_2},\ldots \] なので、\(n_1,n_2,\ldots\) の最小数を、\(n_m\) とすれば、それが求めるべき \(m\) である。

ということなのだが、実は、これを Hilbert は、次の様な不思議な議論で証明している。\(a_1x^{r_1}\) を、係数が0でない最初の form だとする。そして、ここから右に form の列を見ていく。指数が \(r_1\) 以上の式はスキップして、ドンドン先に進む。そして、\(r_1\) より小さい指数の式 \(a_ix^{n_i}\) に遭遇したら、その \(n_i\) を \(r_2\) とする。同様にして、\(r_1,r_2,r_3,\ldots\) を定義するが、自然数の真に下降する列なので、無限に続くことは無い。つまり、ある時点でこの列は停止する。つまり、\(r_m\) で、残りの列の指数のどれも、これより小さいものがない \(m\) が得られる。これが求めるべきものである。

この議論は、現代からみれば実に無駄で意図がわからない不思議な議論に見える。しかし、この議論の背景に数学基礎論的な思索があった可能性がある。既に講義資料2で、ドイツ数学会の不変式論のモノグラフで、Franz Meyer は、現代の我々には何の違和感もない、Cantor の基本列、つまり、有理数のコーシー列と同じ様なものを使うので、科学的な証明でないという意見もあると言う意味のコメントしていることを紹介した。Dirichlet的な「任意の関数」とか「任意の無限列」の様な考え方は、まだ完全な市民権を得ておらず、Hilbert は、そういう反対意見への予防線として、彼の証明をなるべく有限的に見せようとしたのかもしれないのである。そして、それは、私の新説のために新たに起きたある歴史の謎と、それへの私の暫定的解答と深く関係するので、それを扱う2.5で詳しく解説することになる。

次に、変数が2個の場合である。まず、\(F_1,F_2,\ldots\) に共通因子があれば、すべての式をそれで割り共通因子が無い様にする(実は、[Hilbert1993]では、この共通因子の除去の所でも、1変数の場合のトライ&エラーと同じ種類の議論を使っている)。そうやってできた列の最初の有限個の式の線形結合(林注：有限基底理定理で考えている \(A_1F_1+\cdots +A_mF_m\) を Hilbert は線形結合と呼んでいる)によって表される form \(G\) と \(H\) で、それが共通因子を持たないものを作る。そして、これら二つの form の次数の和を \(r\) とする。\(r\) 以上の次数を持つ任意の form は、適当な form \(A_1,A_2\) を取れば \[ F=A_1G+A_2H \] と書ける。もちろん、列の中の form もそうである。また、列の form で次数が、\(r\) より小さいものは、本質的には有限個しかないので、それらと、\(G,H\) を作るために使った form を全部含む様に \(m\) を決めればよい。

変数が3個の場合は、Max Noether の基本定理を使うが、証明は非常に面倒になると書かれているが、その詳細は不明である。しかし、Hilbert は[Hilbert1893]で使用した零点定理を、この Noether の定理の一般化として捉えており、彼の数学ノートブックには、それを追求せよというメモが多く見られる。その事から、この様な所から[Hilbert1893]を構想した可能性があるので、是非知りたいのだが、林には何を意味しているのかが分からない。

ここで、三変数で既に直接証明が難しいことを強調し、そのため変数の数についての数学的帰納法による証明に方針を変えると Hilbert は宣言する。読んでいると肩透かしを食らったようで、変な気がする部分である。最初から、数学的帰納法でやれば良いのにと思うが、何か強い思い入れがあるのか、この説明の仕方は、1897年の講義[Hilbert1993]でも繰り返されている。

1.2.2. Theorem I の証明

ということで、ここから Theorem I の数学的帰納法による証明になるわけだが、\(n=1\) の場合は、すでに証明できているので、\(n-1\)変数の場合に定理が正しいとして、\(n\)変数の場合を証明することになる。変数は \(x_1,\ldots,x_n\) だとしよう。これに対する有限基底定理を \(x_1,\ldots,x_{n-1}\) に対する有限基底定理から証明する。Hilbert の証明の議論は正確ではあるが、形式的で分かりにくいので、[Grace&Young1903]を参考にして少し解り易い形で証明する。

まず、可逆な線形変換による変数変換により、与えられた form の無限列の中に、その次数が \(r\) であり、また、\(a\not=0\) となる \(ax_n^r\) という項を含む form が少なくとも一つあるとしても一般性を失わないことがわかる。そこで、その前提で議論することにして、その様な form のひとつを選んで \(H\) とする。

列の任意の form \(F_i\) を \(H\) で「割り算」して、次の様に変形する。 \[\tag{1} F_i=HP_i+M_ix_n^{r-1}+N_i. \] ただし、\(M_i\) は、\(x_n\) を含まず、\(N_i\) は、\(r-1\) 次以上の \(x_n\) を含まないとする。

\(x_1,\ldots,x_{n-1}\) の form の列 \(M_1,M_2,\ldots\) ができたので、これに帰納法の仮定を適用し、 任意の \(i\) に対して、 \[\tag{2} M_i=B_1M_1+\cdots+B_kM_k \] となる form \(B_1,\ldots,B_k\) が存在するような \(M_1,\ldots,M_k\) を選ぶ。

(1) より \[\tag{3} x_n^{r-1}M_i=F_i-HP_i-N_i \] なので、(2) の両辺に \(x_n^{r-1}\) を掛けて、この等式で代入すると、 \[ F_i-HP_i-N_i=B_1(F_1-HP_1-N_1)+\cdots+B_k(F_k-HP_k-N_k) \] なので、任意の \(F_i\) は次の様に表現できることがわかる。 \[\tag{4} F_i=\{H(P_i-B_1P_1-\cdots-B_kP_k)+B_1F_1+\cdots+B_kF_k\}+[N_i-B_1N_1-\cdots- B_kN_k]. \] ここで、右辺が \(\{\ldots\}\) と \([\ldots]\) という二つの部分に分かれたことに注意しよう。

この時、\(\{\ldots\}\) は、\(H,F_1,\ldots,F_k\) という、与えられた form の列 \(F_1,F_2,\ldots\) 由来の form の「線形結合」、つまり、\(A_0H+A_1F_1+\cdots+A_kF_k\) という形である。従って、残りの部分 \([\ldots]\) を、この \(H,F_1,\ldots,F_k\) に幾つかの \(F_i\) を追加することにより、その「線形結合」で表現できれば、目的の結論が得られることとなる。

ところで、\([\ldots]\) の部分の項には、\(r-1\) 次以上の \(x_n\) が含まれていない。そのため、(4)は、次の形に書ける。 \[\tag{5} F_i=\{\ldots\}+M_i^{(1)}x_n^{r-2}+N_i^{(1)} \] ただし、\(M_i^{(1)}\) は、\(x_n\) を含まず、\(N_i^{(1)}\) は、\(r-2\) 次以上の \(x_n\) を含まないとする。

これは、(1) を \[ F_i=\{HP_i\}+M_ix_n^{r-1}+N_i \] と考えれば、同じ形で、しかも、\(x_n\) の次数が一つ下がっている。また、(3)から(4)を得たプロセスを検討すると、(1)から(5)を得たプロセスと同じことを、(1)の代わりに(5)を使って行えることがわかる。その際、(2)を得るためには、\(M_1^{(1)},M_2^{(1)},\ldots\) に対して帰納法の仮定を適用することになるが、異なる列への帰納法の仮定の適用なので、その \(k\) は、最初の \(M_1,M_2,\ldots\) に対する \(k\) より大きいかもしれない。そうすると、基の「候補」が、\(H,F_1,\ldots,F_k\) より有限個増える。

結局、この二度目のプロセスにより、今度は \(M_i^{(2)},N_i^{(2)}\) が得られる。同様に、\(M_i^{(r)},N_i^{(r)}\) を得るまで同じことを繰り返すと、これに対しては、(5)に当たる式が、 \[\tag{6} F_i=\{\ldots\}+M_i^{(r)}+N_i^{(r)} \] で、\(N_i^{(r)}\) は、0次以上の　\(x_n\) を含まないことになるが、それは結局、\(N_i^{(r)}\) も \(M_i^{(r)}\) と同様に \(x_n\) を含まない式だということになる。

従って、\(M_1^{(r)}+N_1^{(r)},M_2^{(r)}+N_2^{(r)},\ldots\) に帰納法の仮定を適用すると、それは先頭の有限個の「線形結合」で表せることになる。 また、それらの全ては、(6)より、最初の \(F_1,F_2,\ldots\) の先頭の有限個の「線形結合」で表せていることになる。この結果、 \(M_1^{(r)}+N_1^{(r)},M_2^{(r)}+N_2^{(r)},\ldots\) の全ての form が、\(F_1,F_2,\ldots\) の先頭の有限個の「線形結合」で表せることになり、これで \(F_1,F_2,\ldots\) の全てが、その先頭の有限個の form の「線形結合」で表せることとなる。 これで証明が完成した。

以上の証明は、極力、アルゴリズム的な操作が明確になる様に書いた。実は、これを子細に分析すると、あの奇妙な \(n=1\) の場合の証明と同じことが起きるのである。つまり、この証明には、ある無限に走り続け停止しないアルゴリズムが隠されていて、それを使って計算を行うと、プログラムの意味での変数 \(k\) に格納されている自然数が段々大きくなるが、それは有限時間内に停滞の状態に入り、その停滞状態の時の \(k\) の値こそ、有限基底定理でもとめるべき、有限の基 \(F_1,\ldots,F_k\) の \(k\) になるのである。これについては、2.5で解説することにして、次にセクションIの残りの部分の内容を解説しよう。

Hilbert は有限基底定理の証明を行った後、Modul という概念を定義する。それは form のシステム、つまり、集合で、\(F_1,\ldots,F_n\) が、そのシステムの要素であるとき、任意の form \(A_1,\ldots,A_n\) に対して、\(A_1F_1+\cdots+A_nF_n\) が、そのシステムに属するようなものをいう。 　　

そして、この概念が、Kronecker のものであることを明かすのである。Kronekcer の理論[Kronecker1882]では、式は同次ではないので、そこが違うことを強調した上で、 セクションIの冒頭の問題は、要するにこの Modul に有限の基があるかという問題だとし、それを Theorem I を使って証明している。証明は、現代的代数に慣れている人には、自明だろうから省略する。

そして、その後、この事実の「応用」を三つ示している。最初の応用は、空間内の曲線を含む曲面のすべてを表せるような式の存在である。ただし、式と言っても、一つの式ではなく、有限個の任意 form をパラメータとするスキームと言った方がよいだろう。また、この論文の式は、すべて form なので、空間は射影空間になる。これはそういう曲面の Modul に有限の基があることから簡単に示せるが、その例として、Hilbert は、3次元射影空間内のある具体的な曲線をパラメータ表示で定義し、それを含む曲面を定義する式を具体的に求めている。普通そういう時には、定理の証明に、その例を適用して、それにより解を求めることが多いわけだが、有限基底定理の証明の性格上、それは無理なので、有限基底定理の証明とは全く関係なく、その空間曲線の具体的な性質を使って解を求めている。二番目の応用は、方程式と解に関するものだったが、この場合も具体的例が与えられているが、同様に、その特殊ケースの条件をもとに解が与えられている。

herehere 三番目の応用は、これらとは性格が異なり、一般的な命題とその証明だった。斉次の連立一次方程式はトリビアルな解を持ち、また、そのすべての解が有限個の特殊解の線形結合で表されることは、高校、あるいは、大学の初年級で複素数体の場合を学んだと思う。同じ問題は、任意の環に対して考えることができて、それが体ならば複素数体の場合と同じに解けることがわかる。今日の資料の最初の方にでてきた Gordan の補題も、そういう問題の整数環の問題で、解を非負整数ベクトルに限定した問題である。

Form は次数が違うと足し算できないので環にはならず、graded ring というものになるが、同じくこういう連立ディオファントス一次方程式の問題を考えることができる。そして、有限基底定理の第3の応用は、form に対する、この問題が肯定的に解けるという命題だったのである。今回は、中心テーマと全く関係がないので説明をほぼ省略するセクションIIIで、Hilbert は、form の間の関係 syzygy について考察し、現在 syzygy 定理と呼ばれているものの最初のバージョンを証明している。この命題は、その syzygy 定理の定式化に必要な 命題だったのである。

ここでも奇妙なことがある。普通ならば定理とか命題あるいは補題とか銘打って提示され証明される程度のまとまった数学的結果が、単なる応用の一つとして提示されている。それは、この論文の Göttingen 紀要の第一速報[Hilbert1888]で、成り立たない命題を定理として示してしまったものの「代替」であった。後で説明するが、Hilbert は、線形方程式のような条件がない、form のベクトルの集合に対しても有限基底定理が成り立つと思ってしまったのである。もし、そうならば、この第3の応用の代わりに、そのベクトルの有限基底定理を使えばよい。しかし、それには反例が存在するのである。

いつ、その誤りに気が付いたのか分からないが、奇妙なのは、その誤りを Hilbert 自身は、どこでも修正していない点である。この第3の応用の箇所で、速報には誤りがあり、この命題で修正すると書けばよいものを、それが書いてない。非常に不自然に感じる。また、その証明は、実に要領が悪く、分かってしまえば簡単なことが、本当に分かりにくく書かれている。これも、この論文の不可思議な所の一つだ。そして、この命題の具体例を考えてセクションIは終わる。

ところで、Hilbert の有限基底定理の証明、特に、Gordan の1899年のバージョンは、Gröbner base の話と深い関係があることが知られている。Gröbner base を計算するための Buchberger algorithm では、何らかの単項式の順序が必要で、指数の辞書式順序が標準的なものの一つであるが、Noether が Gordan への追悼論文に書いた、Gordan が式を並べるために使った順序というのが、辞書式順序に由来するものだったのである。現代の有限基底定理は、環に対して定式化されることが多いので、上の証明との比較は無理なのだが、Gröbner base と絡めて、有限基底定理が教えられるときには、上の証明とよく似た leading term が生成するイデアルを使う証明が使われることがある。この Cornell 大学の代数幾何学の代数幾何学のコースの　Lesson 10 の handout が、その典型で、\(ax_n^r\) を使う所など、よく似た証明であることがわかると思う。

1.2.3. セクションIIの内容：整数上の有限基底定理

[Hilbert1890]のセクションIIは、Hilbert の革命的不変式論、あるいは、それを越えた form の理論のルーツだった整数係数の form の有限基底定理である Theorem II のステートメントと証明だけから出来ている。そして、最後に、数論への応用があるかもしれないが、この論文では、その問題は扱わず本題にもどる、と素気なくセクションIIは終わる。しかし、その後、Hilbert が、この定理を使って数学を行った形跡はない。もちろん、この論文でも使われることはなかった。また、1897年の不変論式講義[Hilbert1993]では言及さえされなくなる。この証明は捨て去られたかのようである。

その Theorem II のステートメントは、次の様なものだった。

セクションの最初で、Theorem I の証明では、割り算が多く使われているので、Theorem II の証明には使えないことが宣言され、新しい証明が必要となることが宣言される。そして、この証明は、Theorem I の別証明としても使えることが告げられる。 この定理は現代的な Noether 環上の有限基底定理と同様に定式化し直せる。整数を可換環に置き換えて、可換環の要素の無限列に対して、有限基底定理がなりたつという条件を加えればよい。証明は、まったく変更なしに通用する。つまり、実はこのセクションで、Hilbert は、後のネーター環上の多項式環の有限基底定理を実質的に証明しているのである。

Hilbert は、この Theorem II の証明を新しい証明と呼び、また、Theorem I より一般的な証明と呼んでいる。しかし、この資料の2.1で、実は、新しいのは Theorem I の証明の方だったことを史料を使って実証する。そうすると、非常に不思議な謎が浮かび上がる。どうして、Hilbert は、より一般的な証明を持っているのに、わざわざ、より狭い Theorem I の証明を考え出し、そして、それに乗り換えて、まるで捨て去ってしまったかの様な態度を取ったのだろうか。これについては、2.5で一応の解答を与える。

この Theorem II の証明には、先に紹介した Theorem I の証明の様な分かり易いバージョンが未だない。Hilbert の証明は、非常に形式的で複雑で長いので、ここで紹介することは避ける。ただ、上に書いた不思議な謎の解明を試みる時に、Theorem II の帰納法による証明のインダクションステップの極く小さい一部だけを示すことになる。

1.2.4. セクションIIIとIVの内容: Syzygy 定理と Hilbert polynomial

セクションIIIの内容は、現在 syzygy 定理と呼ばれているもののルーツにあたる定理と、その証明であった。先に Theorem I の三つの応用の話をしたが、その最後のものが、これである。Syzygy という言葉は、relation と同義の英語で、Cayley などの古い論文にも見られるが、要するには、その応用の話の際に説明した、form を係数と未知数とする斉次一次連立方程式を form の間の関係と見なすのである。 そうすると、第3の応用により、syzygy は本質的に有限しかないことが判るので、それらの間の方程式、つまり、syzygy を考えることができる。ということで、これは何度でも繰り返せるわけだが、繰り返していくといつか、syzygy は消滅してしまう、というのが Hilbert の syzygy 定理であった。

また、セクションIVは、現在 Hilbert polynomial と呼ばれているものについてのセクションであった。Hilbert 自身は、これを Modul の特徴関数と呼んでいる。Weight と degree を固定すると、不変式が有限次元のベクトル空間を成すというのを宿題(の略解)でやったが、それと同じように Modul の基の数を考えるのが、このセクションの目的であるが、syzygy 定理が、現代のホモロジー代数の源流のひとつとされているのに比べ、これは現在では殆ど知られていないようなので、これ以上の説明は避ける。

これら二つのセクションの結果は、 Gordan 問題の解決とは直接の関係はない。どちらも、不変式論への応用はあり、たとえば後者の方は、次数などを固定した場合に不変式を枚挙したり、その数を数えるという Sylvester の問題へのひとつの答となるし、論文の巻末には、不変式論のコンテキストでの syzygy の問題が議論されている。しかし、これら二つは、Gordan 問題の解を与えるためには必要ないのである。

一般向けの解説の中には、syzygy 定理が、Gordan 問題の解決に使われた様に書かれているものがあるが、これは間違いである。ということで、今回のテーマに、この二つのセクションは関係がないので、その説明は、これだけで終わる。

1.2.5. セクションVの内容: Gordan 問題の解決

このセクションが、[Hilbert1890]唯一の不変式論に関係するセクションである。Hilbert は、Klein の示唆に従い、Gordan 問題の解決という彼を一気に大数学者のレベルに高めた成果を、この論文の応用の一つに過ぎないという風に論文をまとめたのである。

それは、Klein がその数学史講義で解説した様に、有限基底定理の広大な適用範囲を示す論文として紹介されるべきものの筈なのだが、少なくとも通俗数学史の筆者たちには、それが理解されていないのは残念な事と言える。ただ、講義資料2で Reid が Cayley が書いた数式を省略してしまい、その為に、誤りが長く発見されなかったらしいことを考えると、通俗数学史の限界なのかもしれない。やはり、数式無しの数学史というのは、どこかに無理があるのだろう。

実は、通俗数学史の筆者だけでなく、高名な数学者が書いた過去を振り返る不変式論の解説でも同じことがある。たとえば、"Invariant theory, old and new"[Dieudonné&Carrell1970]でも、次の様に書かれている。

But this had only been proved (by Gordan, 1868) for binary forms. The proof by Hilbert (in 1890) of the general conjecture created therefore a big sensation, all the more so since Hilbert did not rely on any computational device, but on general finiteness arguments (the famous “Basissatz” which he proved in the same paper) and on a process associating an invariant form to a noninvariant one (the \(\Omega\)-process of Cayley). (強調は、林による)

では、セクションVの内容を見て行こう。Hilbert は、彼の Theorem I の力が、特に大きく発揮される場とし不変式論があるとして、Gordan 問題の解決について語り始める。ところが、ここでも、Theorem I の証明の前に、1から3変数の場合の個別な証明が説明されていたように、Gordan 問題、Cayley の予想を解決する証明の前に、binary の場合の「特別」な証明の話が差し込まれる。それは、彼の博士論文の結果を使うと、binary の場合には、有限基底定理から非常に簡単に Cayley の予想が証明されるという話である。つまり、Gordan 定理の別証明である。実は、これが直ぐ後の林の新説の要になる「忘れられた証明」あるいは「捨てられた証明」の痕跡なのである。その話は、新説の2.1で詳しくするので、今は、その部分を飛ばして、次に進もう。

そこで、上の Dieudonné たちの引用で、"the \(\Omega\)-process of Cayley" と書かれている Gordan 問題への回答の話である。これは、既に、講義資料2で、H-process という言葉を勝手に作って、それと有限基底定理をどう組み合わせ Gordan 問題を解くのか説明済みなので、私が H-process と呼んだ、その操作の説明だけを行う。

講義資料1で、Cayley の \(\Omega\)ｰprocess は説明済みだが、それは covariant に対する操作だった。しかし、この論文で Hilbert が考えているのは、invariant のみである。invariant に講義資料1の \(\Omega\)ｰoperator \[ \Omega = \begin{vmatrix}\frac{\partial}{\partial x_{11}} & \frac{\partial}{\partial x_{12}} \\ \frac{\partial}{\partial x_{21}} & \frac{\partial}{\partial x_{22}}\end{vmatrix}= \frac{\partial}{\partial x_{11}\partial x_{22}}-\frac{\partial}{\partial x_{12}\partial x_{21}} \] を適用しても、\(x_{ij}\) の様な ground form の変数が含まれていないので何も変わらない。

そこで、Hilbert は、Clebsch や Gordan に由来するというテクニックを使って、\(\Omega\)-operator を invariant に適用出来るようにした。 まず、同じ \(\Omega\) という記号で書くが、本来の \(\Omega\)-operator とは違う、次の様な operator を定義する。 \[ \Omega = \frac{\partial}{\partial \alpha_{11}\partial \alpha_{22}}-\frac{\partial}{\partial \alpha_{12}\partial \alpha_{21}} \] この \(\alpha{ij}\) が何かというと、不変式を定義するときに使った、あの線形変換 \begin{equation} \begin{aligned} x_1 & = \alpha_{11}x_1'+ \alpha_{12}x_2', \\ x_2 & = \alpha_{21}x_1'+ \alpha_{22}x_2' \end{aligned} \end{equation} の係数なのである。

しかし、不変式は ground form の係数の式なので、この新しい \(\Omega\) を適用しても、やはり何も変わらない。そこで、ground form \(f\) \[ f=a_0x_1^2+2a_1x_1x_2+a_2x_2^2 \] に上の線形変換で代入を行い、\(x_1',x_2'\) の form に変換する。それを次の \(g\) としよう。 \[ ｇ=b_0{x'}_1^2+2b_1{x'}_1{x'}_2+b_2{x'}_2^2 \] この \(g\) の係数 \(b_i\) には、\(\alpha_{ij}\) が含まれている。そこで、元の ground form の係数の多項式ではなく、この \(g\) の \(b_i\) の多項式に新しい \(\Omega\)-operator を適用するのである。

Hilbert は、この新しい \(\Omega\) に対して、次の三つのことが成り立つことを示した。

1. \(F(a)\) が \(a_0,a_1,a_2\) の任意の多項式で、\(\pi\) が任意の非負整数であるとする。係数行列 \([\alpha_{ij}]\) の行列式を \(\epsilon\) とすると、\(\epsilon^\pi F(b)\) に \(\Omega\) を何度も適用して、\(\alpha_{ij}\) がすべて消えたならば、それは不変式になる。ただし、\(F(a)\) とは、ground form の係数 \(a_i\) の式という意味で、\(F(b)\) は、それに形式的に \(b_i\) を代入したものである。
2. 任意の不変式 \(I(a)\) に対して、ある有理数 \(c\) が存在し、\(cI(b)\) に、1 の操作を適用すると、元の \(I(a)\) となる様にできる。
3. \(F,I\) が、それぞれ 1 と 2 のものであるとき、その積に対して、同じ操作を適用すると \(JI\) という形の式になる。ただし、\(J\) は不変式である。

この後、Gordan 問題の解が、後期資料2でアウトラインを示した様に証明され、講義資料1で注意した様に、covariant に対する Gordan 問題、そればかりか contravariant などにも適用できることが注意されて、それにより、この論文の本体は終わる。

そして、その後に数ページにわたって、この新しい理論の光の元、どの様な新たな研究課題が立ち上がるか、数ページに渡って熱の籠った議論が続くのだが、ここではその話は省略して、次に、この[Hilbert1890]までの Hilbert 不変式論の展開の歴史についての林の新説に話題を移す。

2. 1890年までの Hilbert 不変式論の展開(新説)

講義資料2の解説でも、マジックを演技の前に、種明かしをするようなことをしてしまっていたが、ここからの解説でも、今朝(12月19日)読み返して見ると、史料的に、ほぼ確実な事と、speculation, interpretation が錯綜した書き方になっている。そういう書き方をする人も多くいるが、私は、出来る限り（完全はもともと無理）分離する方針なのだが、今回のものは、まだ、研究が進行中で、それが出来ていない。今後、sort out する予定なので、その点はお許しを乞いたい。

ここから、講義資料2で説明した Hilbert 不変式論の「定説」の誤りを修正した、私自身の新説を紹介していく。「定説」と、史料との矛盾点を確認しよう。講義資料2で示した様に、それは二つあった。

一つは、定説では、1888年3月21日に Leipzig 滞在中の Hilbert が、Klein に送った書簡で、同じく、Leipzig に滞在していた Gordan の助けもあり、Gordan 定理、つまり、binary の場合の Cayley の予想の別証明を一つ見つけたと報告した事になっているが、実際の書簡では複数形になっていた。つまり、二つ以上別証明を見つけた、と報告したわけである。

講義資料2のその箇所の画像、翻刻、英訳を再掲しよう。

Unter der anregenden Hülfe des Herrn Professor Gordan ist inzwischen eine unendliche Reihe von Gedankenschwingungen in mir erzeugt und insbesondere habe ich, so glauben wir, herrlich kurze und pointirte Beweise für die Endlichkeit der binären Formensysteme.

With the stimulating help of Professor Gordan, an infinite series of thought-vibrations has been generated in me and in particular I have, we believe, wonderfully short and pointed proofs for the finiteness of binary form systems.

もう一つは、1890年2月24日の Gordan から、Klein への書簡で、「Gordan が Leipzig で Klein に Hilbert の証明方法を気に入らないと告げたはずだ」と書いたことになっているのが、実際には、「Gordan が Leipzig で Hilbert に Hilbert の証明方法を気に入らないと告げたはずだ」と書いていることであった。

"ihm" の青枠を除いた画像を再掲する。

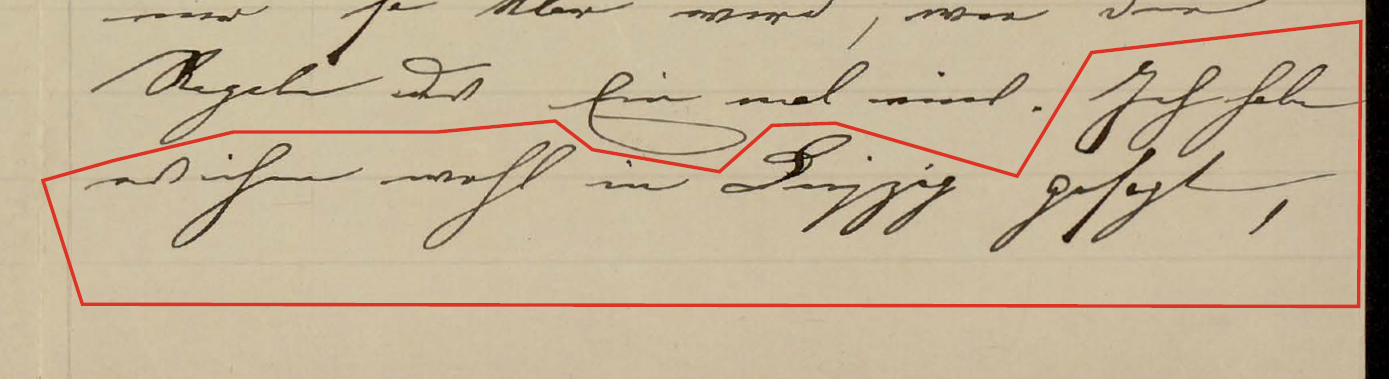
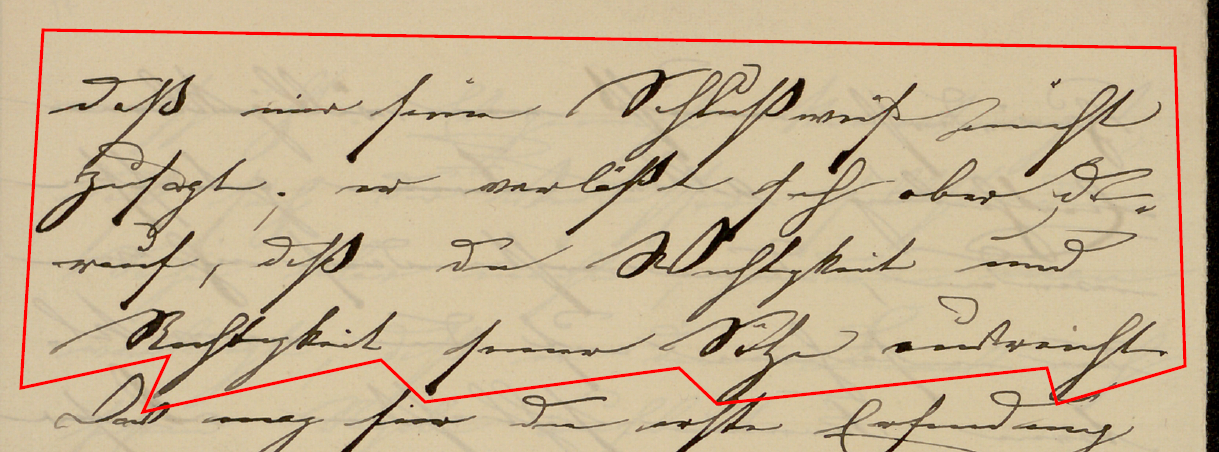
Ich habe es ihm wohl in Leipzig gesagt, dass mir seine Schlussweise nicht zusagt; er verlässt sich aber darauf, dass die Wichtigkeit und Richtigkeit seiner Sätze ausreicht.

I did tell him in Leipzig that I did not like his way of reasoning; but he relies on the importance and correctness of his statements being sufficient.

この二つの矛盾点を、現在、入手可能な史料と整合化する解釈を見つけるということが課せられたタスクである。その私なりの解を、ここから示す。

2.1. 1888年3月 Leipzig: Gordan 定理二つの別証明。

Gordan が、当初、[Hilbert1890]の Theorem I の non-constructive な証明を嫌って、それを神学と呼んだという、Klein の19世紀数学史講義での発言に基づけば、Leipzig での Gordan の Hilbert の証明方法への批判は、それ、または、それに類する証明を見た上での発言と理解するのが自然だろう。

しかし、それは、Theorem I の証明ではあり得ない。1890年3月3日の Hilbert から Klein への書簡で、Hilbert が、Theorem I は、1888年の冬のセメスターに考えたと書いているからである。一方で、Hilbert が Leipzig で Gordan に合ったのは、その年の3月である。

Hilbert は同じ書簡の同じ部分で、さらに、Leipzig で Gordan と議論したのは、[Hilbert1890]のセクションIIの Theorem II の証明だけだ、と書いている。つまり、この史料が、整数版の有限基底定理が、すでに1888年3月に存在していたことを証明しているのである。ただし、これだけでは、二つの Gordan 定理の別証明が何かは分からないということにも注意して欲しい。H-process にあたるものが不足しているからである。

そして、詳しい紹介はしなかったが、Theorem II の証明も、non-constructive であった。つまり、Gordan の批判は、この Theorem II の証明へのものだったと考えるのが最も自然だろう。

以上の考察の根拠として、1890年3月3日の書簡の該当部分の画像、その翻刻と英訳を以下に示す。GDZ製作の書簡全体のPDFファイルは、こちらである。

Uebrigens habe ich niemals über diesen Beweis mit Herrn Professor Gordan gesprochen - denn derselbe ist, wie gesagt, in der vorliegenden Gestalt erst während die$es Semesters entstanden. Während meiner Zusammenkunft mit Herrn Professor Gordan in Leipzig war, soweit ich mich erinnere, nur von dem Beweise des Theorems II (in Abschnitt II) die Rede.

Incidentally, I have never spoken about this proof with Professor Gordan - because, as I said, it was only created in its present form during this semester. During my meeting with Professor Gordan in Leipzig, as far as I remember, only the proof of Theorem II (in Section II) was discussed.

Gordan は、Leipniz で Hilbert から聞いた Theorem II の証明をかなり嫌ったものと思われるが、講義資料2で紹介したように、Hilbert は、あまりネガティブに捉えず、Klein に、次の様に伝えたのだろう。

Trotz mancher abweichenden Anschauung verstehen wir uns doch, glaube ich, recht gut. ([Fei1985], p.38)

Despite some differing views, I think we get on quite well.

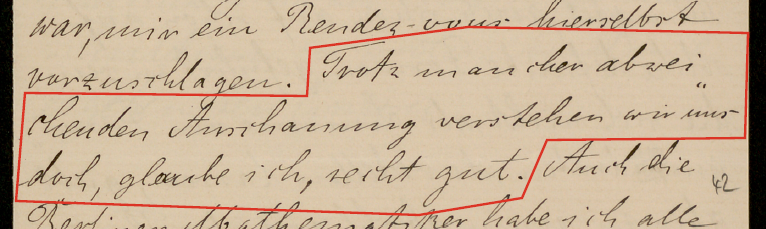
Hilbert が Gordan の彼の証明方法への批判を、あまりネガティブに受け止めなかったのだろうと書いた。しかし、実は、その数学的批判は真剣に受け止めた可能性が高いのではないかとも思う。つまり、批判は強く、それに Hilbert が反応するほどのものだったが、それでも人間関係全般としては、上手く行ったのではないか、それが上に示した "Despite some differing views, I think we get on quite well." の意味ではないかというのが、私の解釈である。

この解釈は小さな事に見えるかもしれないが、私としては、これから説明していく、重要な問題に関係していると考えている。 2.5で、新説最大の謎である、どうして Hilbert がより一般的な Theorem II の証明で満足せず、Theorem I の証明を考え出し、それを自分の理論の中心にすえたのかということを議論するが、予告編のようにそのポイントを説明すると、Hilbert は Gordan の批判を受け入れ、Theorem II の証明を改善した。それが、Theorem I の証明だったのではないかと思うのである。それが、直ぐ上で示した、Theorem I の証明を､Gordan と議論したことはない、議論したことがあるのは、Theorem II の証明だけだという Hilbert の書き方に反映されているのではないかと思うのである。つまり、 Leipzig での、Gordan の批判を受けて証明を改善したのに、その改善した証明に対し、Gordan が、「Leipzig で既に批判したではないか」というのは的外れで理不尽だ、というのが Hilbert が言いたかったことなのではないかという解釈である。

では、そういう強い批判にも関わらず、Hilbert が、それでも Gordan との関係は良好だと思うと書いているのはどうしてだろうか。これも、証明が二つあったので十分理解できることである。一つの証明は、Gordan の気に入らないものであっても、もう一つの証明は、Gordan 自身のディオファントス方程式についての定理が、証明の最大の要として使われていた。Gordan の気分が悪かろうはずがない。

Hilbert の証明は「根の差」を使うので、Gordan が超越的と考える代数学の基本定理を使うことになるので、あまり気がのらない部分があるものの、Gordan 自身が、不変式論講義で、兎に角、それを使っているわけである。自分の複雑だがアルゴリスミックな証明に代わる非常に短い超越的証明があるということを若者が、自分の定理を使って発見したということは、むしろ、気分が良い事であったろう。それは、むしろ自分が成したことのアリゴリズム的意味を際立たせる。それに気分の悪い方の証明は、未だ、自分の binary の場合の定理を越えてはいない。まあ、良いか、という態度で、Gordan が Hilbert に全般としては暖かく接していたとしても何も不思議はないと思うのである。

証明が二つあったという事実は、この様な小さな謎を解く鍵にもなりえる。では、そのもう一つの証明とは何だったのだろうか。幸いなことに、この謎は今の議論の様な推測ばかりではなく、ほぼ確実な史料的裏付けをもって解明できる。実は、Hilbert は、それをちゃんと出版しているのである。ただ、syzygy 定理の定式化に必要となる form の線形方程式の一般解の存在定理の様に、平の議論の中でしか言及せず、番号や名前がついた命題や定理にはしなかった。そのために、見過ごされてしまっていたようである。 そして、それは1890年の論文の三つの速報の内、第3速報にある。そこで、次に、この三つの速報について簡単に解説し、その後、第3速報の Gordan 定理の第2の別証明について説明しよう。

2.2. 三つの速報: [Hilbert1888],[Hilbert1889b,c]

既に説明したように、Hilbert は1890年の Annalen 論文の前に、三つの速報を Göttingen 紀要に投稿している。[Hilbert1888],[Hilbert1889b],[Hilbert1889c]である。リンクしてあるのは、GDZ版の原史料のPDF版である。その内容は、Annalen 論文と若干異なるので、それを説明しよう。

最大の相違は、Annalen 論文では、論文の最後のセクションVで初めて不変式論への応用が語られるのに対して、Gordan 問題の解決が第1速報で述べられている点であろう。もう一つの特徴的な差異は、Theorem I は、[Hilbert1890]と同じだが、Theorem II というものがあり、これが宿題4で反例を考えてもらった命題になっている点である。そして、Hilbert は、この二つを同時に証明する数学的帰納法による証明の粗筋を書いている。その証明は、Theorem I のn変数の場合を仮定して、Theorem II のn変数の場合を証明し、そして、それを使って Theorem I の\(n+1\)変数の場合を証明するというものだが、その証明は間違っていたのである。 つまり、第一報の有限基底定理の証明は間違えていたのである。

その後、Hilbert は、この講義でいう H-process を定義し、それと Theorem I を組み合わせると、Gordan 問題が解けることの概略を説明している。その後、[Hilbert1890]のセクションIの応用とほぼ同じことが紹介されているが、syzygy 定理定式化のための補題は、Theorem I からではなく、Theorem II から自明とされる。おそらく、Theorem II を考えたのは、この補題の証明のためだったのだろう。フルペーパーでの syzygy 定理定式化のための補題は、本当は、シンプルなはずの証明が、非常に分かりにくく書かれている。理由はわからないが、Hilbert は、この補題の証明か、あるいは、その記述方法に困難を感じたのかもしれない。その事が、成り立たない Theorem II を導入させてしまったのかもしれない。

第2速報は、フルペーパーのセクションIII,IVに対応している。そして、問題の第3速報であるが、それは、フルペーパーの Theorem II に対応する Theorem VI で始まる(三つの速報で、定理番号は通しになっている)。そして、非常に詳しく証明が示された後、p.36 で、それは第1速報で行ったと同じ方法で Gordan 問題の解決に使えると説明される。

Auf Grund des eben bewiesenen Theoremes läat sich, wie in der ersten Note gezeigt worden ist, der Nach weis führen, daß die Invarianten eines beliebigen Systems von Grundformen mit beliebig vielen Veränderlichen jederzeit ganze und rationale Funktionen einer endlichen Anzahl derselben sind.

On the basis of the theorem just proved, as shown in the first note, it can be demonstrated that the invariants of any system of basic forms with any number of variables are always whole and rational functions of a finite number of them.

証明方法は書いて無いが、明らかに、次の様なものであろう。

1. 講義資料1で説明した symbolic method の bracket monomial を通常の form に変換したものの係数は整数である。不変式論の第一基本定理により、それらは不変式の基となる。それに Theorem VI を適用して有限個の基を選ぶ。
2. Theorem I による Gordan 問題の証明の場合と同じく、これに H-process を適用する。そうすると、H-process の定義から、process の結果は、有理係数の form になることが簡単にわかる。
3. そのままでは、Theorem VI は適用できないが、適当な整数を掛ければ、係数を全部整数にできるので、それに対して、Theorem VI を適用できる。
4. この様にして Theorem I による Gordan 問題の解決に必要な操作の繰り返しを再現できるので、Theorem VI でも Gordan 問題は解決できる。

2.3. 忘れられた証明: [Hilbert1889c]

そして、この Theorem VI による Gordan 問題の解決可能性の後に、極めて興味深い主張が書かれているのである。それは、次の様なものであった。

Für binäre Grundformen läßt sich dieser Beweis in eine besonders einfache Fassung bringen, wenn man sich des folgenden in der Inauguraldissertation 1) des Verfassers bewiesenen Satzes bedient:

For binary basic forms, this proof can be put into a particularly simple form by using the following theorem, which was proven in the author's inaugural dissertation 1):

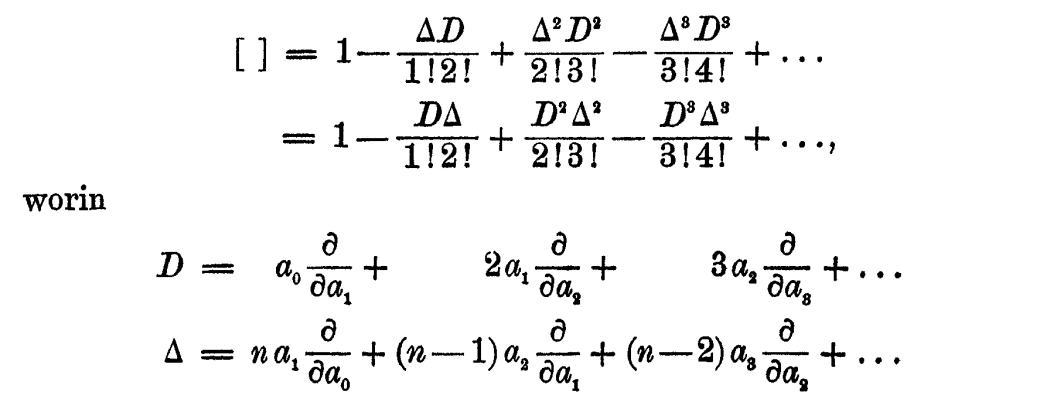
講義資料1で、式の添え字の付け方の重要性を説明するときに、isobaric という概念を使った。つまり、各項を指数を使わず変数の積だけの形にしたとき、現れる変数の添え字を全部足したときの数である重さが、すべての項で一致することを isobaric と言うのであった。

binary な ground form の係数の同次式で isobaric な form に、上の Img-8 の微分演算子 [ ] を適用すると、それは不変式になる。また、この作用素は、不変式に適用すると、その結果は、元の式のままなのである。H-process に似ているが、H-process では、不変式への操作の結果が、有理数倍になるので、こちらの方がスッキリしている。また、不変式 \(I\) に対して、\([AI]=[A]I\) も成り立っていた。H-process というのは、この [ ] を何とかn変数の場合に拡張するために考えられたものだったのだろう。

ちなみに、1893年に Story というアメリカの数学者が、これを一般の場合に拡張している。それまで、これは binary の場合にしか適用できなかったのである。ただ、Hilbert は、博士論文の脚注に、n変数の場合に拡張できると書いている([Hilbert1978],p.2の脚注)。速報の Theorem II と言い、良く間違える人だったのである。

奇妙なのは、その間違いを、Hilbert は後の論文など一切言及しないのである。普通は、この論文でこう書いたのは間違いで、この様に訂正するというをどこかに書くのが常識だと思うが、色々と調べてみても、そういう訂正がないのである。実は、第一速報の Theorem II でも、そうなのである。それが間違いだとハッキリ指摘されたのは、おそらく、Hilbert の全集が出版された時、その editor によって指摘されたのが最初であろう。そういう人だったらしく、その性癖が後の数学基礎論の時代には、相当な混乱を招いているとも思う。

話を戻そう。不変式は isobaric となる。実は、isobaric であるということは、正則な2次正方行列のすべてでなく、その内の対角行列となるものが成す部分群に対して不変性を持つ式だからである(例えば、[Hilbert1993],p.22)。

そして、isobaric は「式の形」で決まってしまうために、少し考えると分かる様に、次の左辺の不変式が、右辺のm個の不変式の「線形結合」で表された時、\(A_i\) は、すべて isobaric だと考えることができる。 \[ \mathcal{I}_i=\mathcal{A}_1\mathcal{I}_1+\cdots +\mathcal{A_m}\mathcal{I}_m \]

これだけ説明すれば、H-process を使う Gordan 問題の解決の時の議論が、この微分作用素を使って、より簡単に行えることが判るだろう。そして、その様な操作ができることは、整数上の有限基底定理を知れば、この作用素を自ら考え出した Hilbert に取っては容易だったに違いない。そして、整数上の有限基底定理が、1888年3月には、すでに証明されていたことは、Hilbert から Klein への1890年の書簡で実証済みである。

つまり、もう一つの Gordan 定理の別証明、「忘れられた証明」とは、第3報で控え目に説明されている、この「整数係数版の有限基底定理と、Hilbert の学位論文の結果の組み合わせによる証明」と考えるのが、最も合理的なのである。ちなみに、[Hilbert1890]のセクションVの解説の際に、「Gordan 問題、Cayley の予想を解決する証明の前に、binary の場合の「特別」な証明の話が差し込まれる」と書いたが、それは、この作用素を Theorem I の結果に適用するという証明だったのである。

2.4. 整数係数版有限基底定理のルーツは?

ここまでの議論で、整数上の有限基底定理とその証明が、1888年3月には、すでに存在していたことが Hilbert 自身により書かれた史料で実証され、また、Hilbert の学位論文と、その1888年版の有限基底定理の、自明ともいえる組み合わせで、Gordan 定理の別証明が得られることから、「忘れられた証明」と見なせるものが第3報に控えめに書かれていた、この組み合わせによる別証明であったであろうことは、非常に高い信憑性を持って示すことができたと考える。

もちろん、第二のものついては、直接の史料的裏付けはないので、今後、異説が生まれる可能性はあるが、おそらく、その可能性は非常に低いであろう。さて、ここから、こういう実証主義的な歴史学ではなく、大幅に speculation と interpretation に依存した議論に転ずる。

既に引用した1890年3月3日の Klein への書簡の内容からして、有限基底定理は、「忘れられた証明」が得られた後の1888年の冬セメスターの間に、Gordan 問題の解決を目指して考えられたのであろう。では、整数係数版の有限基底定理を Hilbert は何を目的として考えだしたのだろうか。果たして、それは不変式論と関係があったのだろうか。

この問に史料的に答えるのは、非常に難しいと思うが、状況証拠からは、おそらく、答はNOだろうと思う。「忘れられた証明」の、微分作用素の結果入る有理数の分母をはらうプロセスは不自然である。わざわざ、その様なものを入れる意味は全くない。そして、それは係数を整数に制限してしまっているからである。つまり、係数を整数とするということは、不変式論的には無駄で不自然なことだとしか言えない。その事を考えると、整数版有限基底定理のルーツは、不変式論以外に求めるのが自然だと思う。

そして、その第一候補は、当然ながら、Hilbert も、Klein も、有限基底定理の代数的枠組みとして認めていた Kronecker の「代数量の算術理論」、つまり、Grundzüge と呼ばれることが多い[Kronecker1882]であったろう。既に述べた様に、この論文で、Kroncker は、それまで揺れていた有理式の係数を整数に固定すると宣言している。つまり、それをさらに ganz, whole な式、つまり整式に制限し、さらに同次に制限したものが、整数版有限基底定理の枠組みであった。

また、1.2.1 で、Hilbert の[Hilbert1890]の論文の始め方が異様であることを指摘したが、あの問題であった、

ある Rationalitätsbereich (domain of rationality) の数を係数とする無限個の form のシステムが与えられた時、その中の有限個の \(F_1,F_2,\ldots,F_m\) を選んで、システムの任意の form \(F\) を、同じ Rationalitätsbereich の form \(A_1,\ldots,A_m\) で、 \[ F=A_1F_1+\cdots +A_mF_m \] と表すことができるかということが問題となる。この問題に決着をつけるために、次の Theorem I を証明する：

Kronecker の Grundzüge [Kronecker1882]は、整数係数の有理式による代数的量の理論であるが、その基本定理は、genus (Guttung) と呼ばれる量の整式のシステムには、同じ genus によるシステムの他のすべての整式を \[ F=A_1F_1+\cdots +A_mF_m \] と表すことができる有限個の整式 \(F_1,\ldots,F_n\) があるという事実が基本定理となっている。この論文は、整式を form に限定し、Kronecker の genus に限らない無限個のその様な form のシステムが与えられた時、Kronecker の基本定理と同様に、常に、その中の有限個の \(F_1,F_2,\ldots,F_m\) を選んで、同じことができるかという問題を考えることができるだろう。そして、この問題に決着をつけるために、次の Theorem II を証明する：

これは、講義資料2の Klein の有限基底定理の意味の説明、『Kroneckerian approaches with Dedekindian thinking により、「すべての代数構造が有限個の代数方程式で記述できることを示すもの」』にも、整数係数であることを除けばピッタリ一致する。そして、Kronecker の場合は、それは1882には係数が整数に限定されていたのである。

これには、もうひとつ、Kronecker 側から、Hilbert の理論を見たときの見え方という、伝聞に基づくものだが、史料的証拠もある。実は、私と共同研究者が、Hilbert の数学ノートブック(参考1, 参考2)の研究をしていた20年ほど前に、当時、私の研究室に所属していた学部学生だった橋本雄太氏(現国立歴史民俗博物館研究部准教授)が発見した、次の様なノートが存在するのである。

Hilbert の3冊の数学ノートブックの内の1である [Wissenschaftliches Tagebuch. Aufzeichnungen zu allgemeinen und besonderen Problemen der Mathematik. 1. Heft], Leipzig, 1885 - 1892の pp.53-54 のノートで、翻刻と英訳が次の様になる。大きいので画像を貼ることはさける。この二つのページのみをPDF化したものが、こちらにある。最初のページの一番下の方にある横線以下と、次のページの最初の横線に挟まれた領域が、このノートである。

Von verschiedenen Quellen (von Minkowski durch Hensel und von Eberhard durch Gutzmer und andere) habe ich gehört, es herrsche in Berlin die Ansicht, "als sei in meiner Arbeiten nicht zu finden, was nicht schon im Kroneckers Untersuchen stände" (Hensel) und "meine Untersuchungen seien nur einer Uebertragung der Kroneckerschen Ideen in die Invariantentheorie (Kronecker selbst soll dies gesagt haben, wie Gutzmer dabei gewesen ist) Ein flüchtiger Blick in meine Arbeit zeigt das Gegenteil: Sogar der übrigens noch gar nicht ei...an[汚れのため読めず] von Kronecker herrührende Begriff eines 'Moduls' ist wesentlich modifirt (duruch die Forderung der Homogenität). Alle weiteren Begriffe und überhaupt alle Methoden und Resultate sind meiner Eigenthum[Eigentum] (insbesondere auch der erste Fundamentalsatz) und ich lasse mir davon auch nicht ein Tüpfelchen nehmen von niemand, wer es auch sei. Vielmehr betrachte ich es als selbstverstaendliche Ehrensache, dass, nachdem ich dies gesagt, jeder anständige Mensch zur Beseitigung dieses offenbaren Irrthums[Irrtums] beiträgt.

I have heard from various sources (from Minkowski on Hensel's and from Eberhard on Gutzmer's and others) that the view prevails in Berlin that "there is nothing to be found in my work that is not already in Kronecker's research" (Hensel) and that "my research is only a transfer of Kronecker's ideas into the invariant theory (Kronecker himself must say this, when Gutzmer was there). A brief glance at my work shows the opposite: even the concept of a 'module', which incidentally does not even originate from Kronecker, has been significantly modified (through the requirement of homogeneity). All other concepts and generally all methods and results are my property (especially the first fundamental theorem) and I will not allow anyone, whoever they may be, to take one small piece of it from me. Rather, I consider it a matter of self-evident honor that, after I have said this, every decent person contributes to the elimination of this obvious error. （Google translate による訳文を、林がかなり変更)

Kronecker が有限基底定理の任意無限列の様なものを考えていたとは中々思いづらい。しかし、2.5で説明する様に、実は Theorem I の証明は、限りなく constructive に近く、その中には、停止せず永遠に出力を出し続けるアルゴリズムが含まれているのである。そして、もし、Theorem I の無限列が、ある n 以後では、同じ form \(F_n\) ばかりになっているとしたら、それは有限列と同じことで、普通のアルゴリズムとみなして実行もできるのである。つまり、そのアルゴリズムは、無限列の先頭の有限列には普通に適用できて、ただ、計算が終わったと思ったら、また、エキストラの入力を渡される、その為に無限に走り続けるしない。そういった種類のアルゴリズムが Theorem I の証明に潜んでいるのである。

その様な列の先頭の有限列に対して適用可能な、Hilbert の Theorem I と同じ様な操作を、Kronecker が考えていたということは排除できない。Hilbert は、Kronecker のアルゴリズムを、無限に入力を増やし続けて走らせているだけだと Berlin の数学者たちが考えたという事はあり得るだろう。もし、そうならば、Kronecker や Hensel の発言は、それほど的外れではないのかもしれない。実際、Hilbert 自身、[Hilbert1890]の中で、syzygy 定理の定式に使われたセクションIの form の線形方程式の一般解のところで、特殊な場合を Kronecker が Grundzüge で行っているという脚注をつけている。

この Hilbert の伝聞が正しいとして、果たして、この Berlin の評価が、どこまで妥当性を持つのか、Kronecker の数学が、まだ十分解明されてないだけに、これからの研究の大きな課題である。また、これに関連して、まだ、講義開始直前に考え付いたばかりで、全く確認がとれないでいるが、先に Gordan の1899年の有限基底定理の別証明と Gröbner base の形態的関連性が、今説明したものと関連しているのではないかというのが、気になっている点で、これは講義が終わったら調べてみたいと思っている。

果たして、本当に Kronecker は Hilbert を先取りしていたのだろうか。ただ、例え、そうであっても、Kronecker の有限の壁を越えて進んだ Hilbert が、20世紀の抽象数学の扉を押し開いたということは間違いがないとも思う。 では、Hilbert に Kronecker 的、あるいは19世紀の代数的な、有限の操作を超えることを促したのは、何なのだろうか。パラドキシカルに聞こえるかもしれないが、私は、それは Gordan なのではないかと思うのである。[Hilbert1889a]の内容を説明した時、「Gordan の補題」という、線形ディオファントス連立方程式の定理を説明した。実は、この定理の本質は、その解を実際に得るために使われる消去法の様なアルゴリズムではなく、普通は Dickson の補題と呼ばれるが、実際には、[Gordan1899]で Gordan が発表していた、ある種の非構成的 combinatorics なのである。

今、\(n\)個の非負整数からできた \([a_1,\ldots,a_n]\) というタプル(ベクトル、順序対、リスト)を考える。これは、Gordan の補題で考えられた解だと解釈することができる。その一方で、これを \[ x_1^{a_1}\cdots x_n^{a_n} \] という単項式と同一視することもできる。そう同一視すると、二つの単項式 \[ m_1=x_1^{a_1}\cdots x_n^{a_n},\quad m_2=y_1^{b_1}\cdots y_n^{b_n} \] があったとき、\(m_1\) が \(m_2\) を割る(因子となる)という事は、結局、 \[ a_1\leq b_1,\ldots,a_n\leq b_n \] と同値である。

つまり、係数1の単項式の割り算、あるいは、積の問題は、その指数のタプルの要素ごとの順序の問題と同じなのである。そこで、単項式 \(m_i\) に対応するタプルを \(t_i\) と書いて、\(t_1\) の各要素が、\(t_2\) の対応する要素以下であることを \(t_1\leq t_2\) と書くことにしよう。そのとき、次の補題がなりたつ。

また、当たり前のことだが、極小元の集合では、その二つの異なる要素は、この順序によって順序づけられない。その様な、二つの異なる要素の対が、いずれも順序が付かないような集合を anti chain という。 この概念を使って、Dickson の補題は、次の様に言い換えることができる。

しかし、実は、この補題は、歴史的に言えば、Gordan によるものなのである。Version 2 は、講義資料2で説明した1899年のミュンヘンでの会議の記録のものを再現したもので、version 3 は、その会議の際に、Gordan が Klein にその原稿を渡した[Gordan1899]版の補題なのである。そこで私は、これを「Gordan の第2補題」と呼びたいと思う。もちろん、これらは Hilbert の有限基底定理を受けて考えられたものである。

数学としては、これでよい、しかし、数学史としての問題は、ここからである。問題は、Hilbert の有限基底定理のルーツは何だったかということだった。Dickson の補題、あるいは、Gordan の第2補題の version 1 を考えてみて欲しい。anti chain が有限であるという事実は中々直観的にはイメージできないのに比べて、version 1 は、証明は別にして、直観で考えるとほぼ自明ではないだろうか。例えば長さ2のタプル、つまり、平面上の座標系を考えて、その整数による格子点を考え、その部分集合をイメージして、それに無限個の極小元があるという状況をイメージするのは無理だろう。少なくとも、私にはとてもできない。

私は、Gordan も同様だったのではないかと思うのである。次は、Gordan が、1873年に彼のディオファントス方程式の方の補題を最初に証明したときの論文[Gordan1873](そのPDF版)の、その該当箇所である。少し大きくなってしまうし、直ぐ後に完全な翻刻と英訳を掲載するので、小さい画像にしてある。大きい方がよければPDFで見て欲しい(p.27)。

翻刻と英訳を示そう。

Ganzzahlige Lösungen. Reducibilität. Sind die Formeln (I) auflösbar und in ihnen die Coefficiei1ten \(a_{ik}\) ganzzahlig, dann kann man ihre Auflösung in folgender bekannter Weise bewerkstelligen.
Unter Lösung versteht man hier ein System positiver ganzer Zahlen, welche die Formeln befriedigen. Die Summe zweier Lösungen ist wieder eine Lösung. Solche Lösungen, welche durch Addition anderer entstehen, heissen reducibel, die übrigen irreducibel. Jede Lösung, deren sämmtliche Zahlenwerthe nicht kleiner als die einer anderen sind, ist reducibel, da die Differenz beider eine Lösung ist.
Sind die irreducibeln Lösungen: \[ \begin{align} &g_{11}\ g_{12}\cdots g_{1r}\\ &\qquad\cdots\\ &g_{\mu 1}\ g_{\mu 2}\cdots g_{\mu r}\\ \end{align} \] dann bilden die Ausdrücke: \[ x_i=g_{1i}y_1 + g_{2i}y_2\cdots g_{\mu i}y_\mu \] wenn die \(y\) beliebige positive ganze Zahlen sind, die allgemeinste Lösung. Es handelt sich um die Aufsuchung der irreducibeln Lösungen, welche ich in der Folge auch Particularlösungen nennen will.

Integer solutions. Reducibility. If the formulas (I) are solvable and the coefficients \(a_{ik}\) in them are integers, then their solution can be accomplished in the following well-known way.
A solution here is understood to be a system of positive integers that satisfy the formulas. The sum of two solutions is again a solution. Solutions that arise by adding others are called reducible, the rest are called irreducible. Every solution whose numerical values are not smaller than those of another is reducible, since the difference between the two is a solution.
If the irreducible solutions are: \[ \begin{align} &g_{11}\ g_{12}\cdots g_{1r}\\ &\qquad\cdots\\ &g_{\mu 1}\ g_{\mu 2}\cdots g_{\mu r}\\ \end{align} \] then the expressions: \[ x_i=g_{1i}y_1 + g_{2i}y_2\cdots g_{\mu i}y_\mu \] if the \(y\) are any positive integers, form the most general solution. Now the matter is to find irreducible solutions, which I will also call particular solutions in the following.

(I)というのは、論文巻頭の斉次線形方程式である。ちなみに、この論文は一般の実係数の線形方程式についてのもので、その最後が整数係数、非負整数解の場合についてだった。要するに、その整数の場合、ある解が、二つの解の和にならないとき、irreducible と呼び、irreducible なものの集合が、一般解、つまり、基を与えると言っている。解の集合は線形性を持つために、irreducible な解とは、極小元となる解である。つまり、解の無限集合の内、極小元が基となるというのだが、証明もせずに、それを有限個として、 \[ \begin{align} &g_{11}\ g_{12}\cdots g_{1r}\\ &\qquad\cdots\\ &g_{\mu 1}\ g_{\mu 2}\cdots g_{\mu r}\\ \end{align} \] と並べて書いている。そして、後は、それを探す方法を見つければ、問題は解けたことになるというのである。

この場合、解の集合に線形性があるので、この irreducible な解の集合というのは、Dickson の補題(Gordan の第2補題)の version 1 の極小元の集合、version 2 の \(B\) なのである。

1873年の証明の上の様な書き方からして、 おそらく、Gordan は、irreducible な解が有限個しかないのは自明に正しいと思っていたのだろう。つまり、Gordan の第2補題のversion 1は、彼に取っては直観的に真な命題だったのではないだろうか。そして、Gordan にとって、こういう問題を解くということは、単に、そういうことが真であることを示すだでけではなく、解を実際に発見するアルゴリズムを見つけることにあったのだろうと思う。Gordan は、Hilbert の有限基底定理論文についての Klein への手紙で、

Ich habe es ihm wohl in Leipzig gesagt, dass mir seine Schlussweise nicht zusagt; er verlässt sich aber darauf, dass die Wichtigkeit und Richtigkeit seiner Sätze ausreicht.

I did tell him in Leipzig that I did not like his way of reasoning; but he relies on the importance and correctness of his statements being sufficient.

その時には、注目しなかった、セミコロン以下を見て欲しい。ここで、Gordan は、｢Hilbert は重要性と正しさだけで十分と思っている」と書いているのである。これは、ちゃんとした証明がないと意味が無いということだと解釈することもできるが、上の Gordan の補題や、その他の Gordan の「証明」の書き方を見ると、ちがった印象をうける。おそらく、Gordan は、数学においては、少なくとも代数においては、代数学の基本定理の様な「正しさ」の保証だけでは、十分でなく、解を実際に見つける方法があってこその数学あるいは代数だ、と思っていたのではないのだろうか。

Hilbert は、Gordan 問題の別証明の Annalen 論文で、Gordan の補題に言及した時、この1873年の論文ではなく、1885年の不変式論講義を引用しているが、Gordan は不変式論講義の方では、irreducible な解という概念の説明せず、解を発見するアルゴリズムだけを書いて、それで終わりにしている(Internet Archive のページ)｡

この Gordan が考えている問題は、高校数学のWEBサイトなどで、2変数の整数係数線形方程式の整数解を求める問題として、その解法が説明されているものの一般化である。そういうサイトの説明では、アルゴリズムばかりが強調されていて、何故、そのアルゴリズムで総ての解が求まるのかとか、式変形の前後で式の同値性が保たれている理由とか、そういうものがおろそかにされていることが多いが、同じ問題を大学数学科の講義で扱っているものを見ると、そういう部分がしっかり考慮されていて、非常に違った印象を受ける。

実は、Hilbert も、この Gordan の補題を、1897年の不変式論講義で、構成的に証明しているのだが、その証明は Gordan のそれとは非常に印象が異なり、現代の大学の数学科の講義資料を連想させるものになっている([Hilbert1993],pp.117-118)。

Hilbert の「神学」とは、この「正しさだけで十分」という数学思想の体現だったと言って良いだろう。実は、Hilbert が、Gordan 問題への取り組みを契機として、意識的に、そう決断したという事が解る史料が幸いにも残っている。それは、Königsberg 時代の不変式論講義の講義ノートである(GDZへのリンク, GDZ 提供のPDF版(PDM))。

画像として示すには大きすぎるので、該当文を赤線で囲んだ該当ページ(pp.193-194)だけのPDFを、こちらに置く。次が、Cod.Ms.D.Hilbert 521, pp.193-4 の該当部分の翻刻である。complicirt は低地プロイセン方言と思われるので、標準ドイツ語で⟨kompliziert⟩と、vollstäyige は書き間違いと思われるので⟨vollständige⟩と注釈をつけた。

Gordan zeigt auch dabei gleichzeitig, wie mann zu einem solch wollständige Formensystem gelangen kann. Doch ist die Methode so complicirt ⟨kompliziert⟩, dass man sie nur in den ersten Füllen bis n = 8 hat anwenden können. Wir haben das vollstäyige⟨vollständige⟩ Formensystem n = 1, 2, 3, 4 aufgestellt und für n = 5, n = 6 noch in §15 noch die Invarianten angegeben. Wir begnügen uns mit den gemachten Angaben, da die gewaltig angeschwollene Litteratur; doch nur weitere Beispiele für die einfönigste und trokenste symbolische Rechnung liefert. Das wichtig und fundamentale ist allein jener Satz von der Endlichkeit der Formensystemene.

At the same time, Gordan also shows how one can arrive at such a complete system of forms. However, the method is so complicated that it could only be used in the first few cases up to n = 8. We have established the complete system of forms n = 1, 2, 3, 4 and given the invariants for n = 5, n = 6 in §15. We are content with what worked out, as the flood of literature only provides further examples of the most monotonous and dry symbolic calculation. The only important and fundamental thing is the theorem of the finiteness of the system of forms.

"vollständige Formensystem", complete form system とは、基のことで、要するに、Hilbert は、

Gordan 定理は、次数が少ない場合にしか、実際の基を生み出すことはない。それ以上は複雑すぎて計算が出来ない。これ以上、同じ様なことをやっても、単調で無味乾燥な symbolic method の計算例を増やすだけだ。重要で基本的なのは、有限性の定理のみである

つまり、私は、Hilbert の有限基底理定理の整数版 [Hilbert1890] の Theorem II のルーツは、Kronecker と Gordan の数学だった可能性が高いのではないかと思うのである。もちろん、それは反面教師という側面が大きい。Kronecker や Gordan が重要視する有限性、計算可能性を、意識的に外すという、Hilbert の若き日の決断が、後の数学、特に代数学を劇的に変えたのである。

これは勿論、一つの可能性に過ぎない。ただの想像、あるいは解釈である。実際、それにはウィークポイントがある。少なくとも、Leipzig で Gordan と議論した時、Hilbert が、Gordan の補題が、彼の Theorem II から簡単に証明できると知っていたとは思えない。1897年の講義の際にも、それらしいことが全く述べられていない。おそらく、この関係は、後に Gordan が発見したのが最初なのだろう。[Hilbert1889a]で Gordan の補題を、1873年の論文ではなく、不変式論講義の方で引用しているので、上に示した 1873年の Gordan の「証明」を Hilbert が読んでいない可能性さえある。

しかしながら、「Gordan の助けもあって」と Hilbert が書いたのは、Gordan の不変式論講義では、とても証明になっていないのを、質問した可能性も高いのではないだろうか。そして、その時、Gordan が、1873年の論文と同じような説明をしたとしたら、それが Hilbert が Klein に書いた、"an infinite series of thought vibrations" を引き起こした可能性はある。つまり、それにより Theorem II の証明が生まれたという可能性はあるだろう。

この林の「有限基底定理のルーツは、Kronecker, Gordan 説」は、邪馬台国九州説、邪馬台国大和地方説の様なもので、その正しさを証明するのは、非常に難しい。まして、新説が生まれたばかりである。これに反する別の説が生まれ、それが切磋琢磨することにより、より真実に近づく、数学と違い、歴史学というものは、そういう弁証法的なプロセスを経てのみ、より正しくなるのである。という、ことで、切りが無いこの説の議論は、これで終わりにして、次に、ある謎と、それへの暫定的答を紹介して、講義資料3を終わることにする。

古いバージョンで、ここにあった宿題は編集ミスです。ただ、見た人は考えてみると面白いと思います。

2.5. 新説最大の謎と暫定的解答

私の新説の最大のポイントは、[Hilbert1890]における Hilbert の書き方が与える印象と異なり、Theorem I より前に Theorem II が証明されていたとする所である。しかし、この説が正しいとすると、大きな謎が生まれる。というのは、Hilbert 自身が書いているように、Theorem II の証明は、Theorem I の証明に転用できるからである。

帰納法のインダクションステップは、何も変える必要が無い。ベースケースだけ変えれば十分だが、Theorem II の証明では、Theorem I の証明の様に、1変数の場合をベースにするのでなく、0変数の場合がベースケースだった。つまり、整数列の有限基底の存在が証明されていたのである。それを今度は体で行うことになる。体の要素の無限列は、その先頭の有限個で線形に書けるということを証明することになるが、もちろん、これはトリビアルで、列の要素がすべて0ならば、最初の0、そうでなければ、最初の0でない要素一つですべて書けるわけである。

また、次の様なこともわかる。Hilbert の Theorem I,II の意味での有限基底の存在が成り立つ可換環を、Hilberitian と呼ぶことにしよう。[Hilbert1890]の Theorem II の証明のインダクション・ステップは、何の改変も経ずに、｢Hilbertian 環上の多項式環は、Hilberitian である」という定理の証明になっている。つまり、簡単に分かるように、それは後の Emmy Noether のネーター環の有限基底定理と本質的には同じものなのである。 代数幾何学の入門講義の資料を見ると、体上の多項式環のネーター性を証明するのに、証明のときだけネーター環上の有限基底理定理を使うというパターンが結構見られるが、Theorem I を、Theorem II の証明で証明するというのは、この現代のやり方と全く同じなのである。

ということは、非常に不思議な状況を生む。その様に1920年代の Emmy Noether の理論を先取りする一般的な証明のトリビアルな改変で Theorem I を証明できるのに、何故、Hilbert は、新たな証明を考え、しかも、それを歴史的論文[Hilbert1890]の中心に据え、Theorem II の証明を、Theorem I の証明より一般的 allgemeine と書きながら、従の位置に置いたのだろうか。

Theorem I が先に考え付かれ、Theorem II が、その後に出来たのだったら、これは、それほど大きな問題とはならない。Theorem I の証明は、II のそれより、少し短く、何よりもっと直観的である。そのために、この講義資料でも、比較的短く証明できたのである。また、Hilbert に取っては、最初に思いついたものには愛着があっただろうし、体で考えているのに、わざわざ除算をさける Theorem II の様な証明をするのは不自然でさえある。

Hilbert は、Theorem I を証明した後、理由は良くわからないが、その整数版を考えて、苦労して証明した。Hilbert が書いているように、整数論に応用できる可能性を考えたのかもしれない。しかし、実際には、それは少なくとも Hilbert に取っては使い道がなかった様である。それは、Emmy Noether の可換環論にいたって初めて意味をもつものだった。元々、Theorem I が先で、それが中心ならば、苦労して考えた Theorem II の証明も読者に見せたかっただけだ。しかし、残念ながら、Emmy Noether により、その価値が見いだされるまで、それは役にはただず埋もれていたのだ、と考えるのは、それほど不自然なことではない。頑張って、複雑なものを生み出したが、後の時代には忘れられた、というのは、数学史に限らず科学史では良くあることなのである。

しかし、現実は違った。Theorem II の方が、先に生まれていたのである。では、どうして、Theorem I の証明を生み出す必要があったのか。

答は、色々と考えられる。その一つが、既にみた Berlin の数学者の態度にあるように、Kronecker からの影響を Hilbert が意識していて、また、Theorem II の証明に非常によく似たものが、Kronecker の理論の中にあり、それを嫌がって、新たな証明を考えたという可能性である。 ただ、これは随分と意地が悪い解釈である。言ってみれば、Hilbert が隠蔽を謀ったといわんばかりの説になる。また、Hilbert が syzygy 定理の定式化に必要な命題によく似たものが、すでに Kronecker の理論にあることを、非常に明瞭に、その証明の箇所まで示しながら脚注に書いているということがある。ただ、先に触れた橋本雄太氏が発見したノートからすると、捨てきれない説であり、いずれにしても、Kronecker の理論と[Hilbert1890]の照合という、これからの課題に取り組めば、その作業を通して、何某かのことは見えてくるだろう。もちろん、Kronecker の読みにくさは有名で、Kronecker の専門家でさえ音をあげるほどなので、果たしてこれに取り組む人がでてくるかどうか、それが問題ではあるが。林はやってみたいとは思っているが、少し読んだ経験から、自分だけでは無理そうな気がしている。

また、もっともアッサリした答は、単に Hilbert が、Theorem II の証明が気に入らなかっただけで、除算も使って、よりスッキリした証明にしたかったというものだろう。私も、これは単独では、一番素直な説ではないかと思っている。ただ、この考え方では、Theorem I のベースケースの、あの不思議な最小数の存在の「証明」の記述の仕方の理由づけが、全くできない。そういうものは気にする必要がないという見方もあるだろうが、Hilbert の数学ノートブックなどの研究に携わったものとしては、この問題は、Hilbert の数学思想を理解する上で非常に大きく重要なものに見えるからである。

話題1や、イントロでも述べたが、あの「最小数の存在証明」と、そっくり形で、Hilbert は、その数学ノートブックに、まさに有限基底定理と同じ時期に、「数学の問題はすべて有限ステップで決定可能だ」という、後の単にモットーだと誤解された "Wir müssen wissen. Wir werden wissen." の数学版を書いている。Hilbert は、このモットーを本当に数学で証明しようとしていたとしか思えないのである。それが最も数学的な形態をとったのが、1920年代の Hilbert program での自然数の形式系の完全性証明という問題であった。そして、そのルーツは古く、まさに、彼の不変式論の時代に遡るのである。

話題1でもリンクしてあるが、こちらである。少し説明すると、あの「最小数の存在定理」と非常に似た問題だと言うことが判ると思う。

今回は、これ以上深くは踏み込めないが、すでに示した Königsberg 時代の不変式論講義での Gordan のアルゴリズムの現実的な計算不可能性への言及と同じ考え方に基づいた発言や叙述を、Hilbert は繰り返し行っており、それが彼の「数学は決定可能だ」という、現代の我々には信じがたい信念に、ある種の合理性を与えていたと思われるのである。

この問題は、私が20年ほど前におこなっていた Hilbert 研究の中心テーマで、その立場からすると、この証明の書き変えには、もっと深い意味があるのではないかと思うのである。それが次に説明する私の暫定的解である。

現在の所、Theorem II の一般的証明の後に、Theorem I の応用範囲が狭い別証明が考え出されたという謎に対する私自身の最有力の解の候補は、「Hilbert は、1888年、Leipzig での Theorem II の証明への Gordan の批判を受けて、それをより constructive にしようとした努力の結果が Theorem I である」というものである。Theorem I、つまり、体上の有限基底定理は、代数学に非構成的証明が本格的に持ち込まれ20世紀抽象数学が生まれ契機となった、というのが普通の認識である。それなのに、ここで言っているのは、Theorem I の証明は、Theorem II の証明より構成的であるということなのである。これはどういうことであろうか。

2.5.1. 排中律の階層と Limit Computable Mathematics

証明が非構成的か構成的かということは、排中律、数理論理学の論理式で書くと \(A\lor \lnot A\) を使っているか否かで決まるとされる。そして、Theorem I では、いたるところで、その排中律が使われている。それにも関わらず、Theorem I の証明は、Thorem II の証明より構成的なのである。 実は、20年前の私と共同研究者の国際会議LICSでの講演論文[Akama et al.2004]で、排中律には階層があることが知られているのである。

そして、その階層の一番低いレベルの排中律のみを使う数学の証明は、ある意味でアルゴリズムで実行できることが、解っているのである[Nakata&Hayashi2001]。それは、基本的には、Hilbert の Theorem I のベースケースの証明の「アルゴリズム」、つまり、自然数列の最小数を求めて、先へ先へと最小数を探し続けるのと同じ動きをするアルゴリズムを証明の中に見つけることができるということで、先に説明した Cornell 大学の代数幾何学の講義録の、有限基底定理の証明の中に、Gröbner base を見るという様な考え方を、良く知られた数理論理学の理論を使って組織的に行えばよいだけである。

LCM Limit Computable Mathematics と私が名付けた、この理論は、プログラムの正しさをコンピュータを使い保証する Program Verification という技術に応用するつもりで考えたものだ。その際、あまり応用には繋がらないとは思ったものの、数学的好奇心もあり作っておいた排中律の階層が、今回、こういう形で応用できのだが、それはある意味では必然で、実は、このLCMというものの発想の最大のソースは、Hilbert の Theorem I のベースケースの、あの奇妙な証明の仕方だったのである。

それを北大で行った数学史の講義で話したのが切っ掛けで、今のAIのルーツである機械学習の最初の数学モデルと関係があることを、専門家に教えてもらえた。そして、それを元に考えたのがLCMだったのである。そのころから神戸大工学部の教授だった私は、大好きな歴史をセミプロの様にやっていて、その Hilbert 研究のお陰で、LCMを着想できたわけである。つまり、数学史がソフトウェア工学に役立ったので驚いた。ところが、その際に知的好奇心から考えた数学的理論が、ブーメランの様に数学史研究の方に返って来て、Hilbert 不変式論史の理解に役立って再び驚いている次第なのである。

この排中律の階層とLCMの話を詳しく行うのは不可能なので、例を使って簡単に説明しよう。P=NP問題という計算機科学の未解決問題を知っている人は多いだろうが、こういうものの全ての先祖が「Kleeneの算術階層の理論」というもので、自然数の集合を定義するときに、何個の全称記号 \(\forall\) や存在記号 \(\exists\) を何重にして使うかというもので、算術集合というものの階層を定義する。

この階層は、twin tower の様になっていて、\(\Pi^0_n\) と \(\Sigma^0_n\) という二つのタワーがあって、\(n\) が付いているものがn階にあたり、見かけ上3階のものが、実は式変形すると2階のものになったりはするが、上の階のものには、決して下の階の集合にはならないものがある。また、横の階、つまり、\(\Pi^0_n\) と \(\Sigma^0_n\) の集合は、それぞれの補集合になっていて、これも決して横の階に属さないものが、それぞれにある、という構造になっている。

排中律の階層というのは、たとえば算術階層 \(\Pi^0_1\) の集合を定義するための論理式 \(A\) に対する排中律を \(\Pi^0_1\)-LEM (Law of Excluded Middle)と呼ぶと、それらの間の構成的自然数論の形式系における論理帰結関係に、算術階層と全く同じものが成り立つというものである。たとえば、横の関係である、 \(\Pi^0_1\)-LEM と \(\Sigma^0_1\)-LEM には、相手のどの排中律の例を使っても証明できないものがあり、 また、その逆が成り立つのである。

そして、この一番低い1階の排中律だけをもつ構成的自然数論で行える数学がLCMなのである。そして、LCMで存在が示された値は、limit computing でその値を求めることができる。入力を与えられると、走り出し永遠に計算を続けて値を出力し続けるようなプログラムがあったとしよう。そうすると入力ごとに、出力の列 \(a_1,a_2,\ldots\) が出来るわけだが、どの様な入力に対しても、必ず \(a_n=a_{n+1}=\cdots\) となる \(n\) があるとき、そういうプログラムが行う計算を limit computing という。つまり、limit computing は、有限時間以内に計算が停滞してしまうのである。そうならば、その値を出力とみなせる。そうやって計算できる関数が limit computable な関数なのである。

これは元々は機械学習の数学理論の概念なのだが、実は、これは Hilbert の Theorem I の数学的帰納法のベースケースの議論そのものだと分かる。つまり、指数の数列 \(r_1,r_2,\ldots\) を受け取ったら、プログラムは、最初は \(r_1\) が最小だと仮定して自分のメモリ(変数)に記録すると共に出力する。そして、次の \(r_2\) に進み、それとメモリの値を比較して、メモリの値が \(r_2\) 以下ならば、メモリの値は変えず、メモリの値を出力して、次の \(r_3\) に進むが、もし、\(r_2\) の方が、メモリの値より小さい場合は、それをメモリに記録し、出力して先に進む。これを永遠に繰り返すと、Hilbert の説明と全く同じことになる。そして、メモリの値はどんどん小さくなるので、どこかの時点で、つまり、プログラムが、最小の \(r_i\) に遭遇した時点で停滞が始まるのである。

排中律を使うと計算が出来なくなると言われるが、実は limit computing ならできるのである。\(\Pi^0_1\)-LEM は、計算可能な関数 \(f(x)\) に対して、「すべての \(x\) に対して \(f(x)=0\) であるか、そうでないか」という形の排中律である。こういうものならば、limit computing で、「すべての \(x\) に対して \(f(x)=0\)」が正しいかどうか判定できるのである。

判定プログラムは、\(f(0)\) を計算して、\(0\) ならば、「すべての \(x\) に対して \(f(x)=0\)」が正しいと仮定して、メモリに true と記録し、それを出力する。そして、次の \(f(1)\) を計算して、\(0\) ならば、同じことを繰り返す。しかし、もし、\(f(1)\not=0\) ならば、メモリに false と記録して、それを出力する。これを永遠に繰り返すのだが、一旦、メモリの値が false になったら、後は何が起きても書き変えない。そうすれば、出力は永遠に true と停滞するか、どこかの時点で反例を見つけ、そこから false と停滞することになるのである。

この単純な仕組みがLCMの仕組みなのだが、20年ほど前に代数幾何学の専門家に手伝って頂いて確認したところ、Theorem I の証明は、LCMの証明だったのである(ただし、[Hilbert1993]の証明をつかった)。そう思って、Hilbert の証明を眺めると、ドンドン増加するプロセスが通信しあいながら計算を進める巨大なアルゴリズムが見えるのである。そして、そのアルゴリズムは永遠に走り続けるものの、何時か停滞し、その値が求めるべき基になる \(F_1,\ldots,F_m\) の \(m\) になるのである。

ところが、Theorem II の証明には、LCMに入らない排中律が使われているのである。それは、[Hilbert1890]の次の部分である。

果たして、この暫定的解答が正しいか、今後さらなる検討が必要である。少なくとも、他の可能性の一つとして考えた、Kronecker の理論に Theorem II の証明と似たものがあるかどうかの検討は必要だろう。また、これも繰り返しになるが、有限基底定理の証明と、Gröbner base との関係も留意する必要がある。これは、Gordan 版の有限基底定理の辞書式順序を用いる別証明ついて言われているらしいが、わたしには、どうも Hilbert の証明自体も、ほぼ同じアルゴリズムなのではないかという気がしてならないのである。今後両者の数学的、あるいは、computer science 的な比較が必要なのではないかと思っている。今後の課題が複数出てきたところで、講義資料3を終り、次の講義資料4では、一転して数学の内容の分析ではなく、数学者たちの間の書簡の分析を通して、神学事件の真相に迫ることになる。