2章. Hilbert 不変式論史(定説編) ver.2025.04.04

この2章では、Hilbert の不変式論についての従来までの定説の説明を行う。定説の説明のために、まず、有限基底定理と、それによる Gordan 問題の解決がどの様なものであったかを数学的に説明し、その後、Gordan 問題解決までの歴史の定説がどの様に語られて来たのかを説明する。また、その定説への異説である、McLarty の説も説明する。ただし、それらは、史料を示しながらの説明となり、それにより定説や McLarty の説に史料と矛盾する点が幾つかあることが明らかとなる。そして、その矛盾を解消するために、どの様に説を立て直すべきかは、3,4章で示すことになる。

また、提示する資料には、林が Göttingen 図書館に依頼して作成してもらった画像がかなりの数あり、それらは、今まで誰も研究していなかったと思われるものが含まれている。それらの分析には翻刻(transcription, 手書き文書を活字文書に起こすこと)が必要であり、それを林がどの様に行っているかも示す。それを林の説の正当性の根拠とする。

東大講義終了後、林の依頼により作成された画像は、すべて public domain になった。これにより、それらを自由に閲覧、掲示することが可能となった。それらの画像は総てPDFファイルとしてWEB上で公開されているので、文献表にURLを含めて情報を書いておいた。また、幸いな事に、これら以外の史料画像で、林の今回の研究の正しさの根拠を示すために必要なものは、これを書いている2025年4月4日時点で、すべてデジタル化されていることが確認できている。技術的な理由で、まだWEB上で公開されていない史料もあるようだが、早晩、公開されるだろう。これにより、原史料を画像として示しつつ、その翻刻、翻訳、解釈をWEB上で語ることが可能となったのである。

1. David Hilbert という人

Hilbert の不変式論の歴史について解説する前に、David Hilbert という人について解説しておこう。また、東大講義のための研究により、私は、従来の Hilbert 像を大きく変える必要があるのではないかと思う様になっている。有限基底定理の研究というものが、彼の数学思想や数学人生にとって、今まで考えられてきたより遥かに大きな意味を持っていたらしいのである。そのことについても触れる。

Hilbert は、1862年1月に、当時のプロイセン王国 Königreich Preußen のケーニヒスベルク Königsberg に生まれた。ケーニヒスベルク大学で数学を学ぶが、ガウスなどと異なり、数学の才能が花開いたのは遅く、1888年、26歳になってのことである。この年、彼に何かが起きて、突然、大数学者に変身する。そして、時期的に見て、このサイトの中心的テーマである、有限基底定理の発見が、その契機であったのは間違いない。

Hilbert は多くの分野で重要な研究を行ったが、その内、最も有名なものを列挙すると、このサイトのテーマである不変式論の研究、特にその中で発見した有限基底定理と零点定理という現代的代数学の基本定理、代数的整数論、幾何学基礎論、積分方程式論と関数解析学の先駆、数学基礎論の Hilbert 計画、であろう。この他にも、Weierstrass により反例が与えられた Riemann のディリクレ原理の合理化などがある。

Hilbert は、この様に多彩な数学分野における個別の成果の他に、数学という学問自体の進むべき道を指し示すリーダーとしての役割を果たした。彼は公理論 Axiomatik という数学理論の展開方法を提案し、これを強く推し進めた。これは後の Bourbaki 流の構造主義の数学の先駆けである。Bourbaki が、[Bourbaki1950]で指摘、あるいは、批判したように、Hilbert の公理論は、そのモデルが本質的に唯一となる範疇性という条件が入っていた点で、現代的な公理論である現代の抽象数学と大きく異なっていた。 また、言語による公理の記述とそれからの証明への依存度が非常に強かった。その Hilbert 公理論から範疇性を除き、「言語と証明」を、構造を保存する写像、つまり準同型写像に置き換えたものが、Bourbaki の公理論であり、さらには準同型の集まりである圏に基づく今日の抽象数学である。

この様に Hilbert の公理論は、現代の抽象数学とはかなり異なったものなのだが、 Bourbaki が、[Bourbaki1950]で自らの数学観を Hilbert 公理論と対比させて語った様に、彼の公理論が Bourbaki 数学の元となったのだから、これが現代数学、少なくとも現代抽象代数学の幕あけを告げるものであったことは間違いない。また、このテキストの中心テーマである有限基底定理、特に、その証明が、公理論的に代数学を推し進める際のパラダイムとなった。そのため、Bourbaki の数学史家だった Dieudonné は、これを「最初の現代代数学」と呼んだのである[Dieudonné&Carrell1970]。この様な次第で Hilbert は「現代数学の父」と呼ばれることがあるし、そう呼ぶことは妥当だと思う^[1]。

ただ、Hilbert が「現代数学の父」と呼ばれるには、もう一つの理由がある。彼は来るべき時代の数学の姿を示す、数学のリーダーでもあった。彼は、折に触れて、数学が進むべき道を示すプロパガンダ的雰囲気さえ漂う講演を行った。それらの内で、特に有名な講演が二つある。ひとつは、1900年の第2回国際数学者会議でおこなわれた Mathematische Probleme 「数学の問題」という講演だ。おそらく、これが彼の講演の中でも最も有名なものだろう。

ただし、この講演が有名になったのは、1900年8月8日に行われた講演そのものではなくて、後に Göttingen Nachrichten で刊行された「講演の拡張版」の論文 [Hilbert1900]によってであった。Hilbert は、この論文で23の未解決問題を提示し、それを20世紀の数学が目指すべき目標とした。20世紀の数学界における、その影響力は絶大で、林が大学生だった1970年代には、この問題が何問解けたかで20世紀数学の進歩の度合いをはかることができると言われていた迄である。

以後、1900年の講演とか、講演「数学の問題」と言ったときには、国際数学者会議における講演ではなくて、この論文[Hilbert1900]のことだと思って欲しい。パリでの講演では、時間の関係で23の問題全部を提示できていないのである。ちなみに、この講演を巡っては、それ以外にも色々複雑な事情があった。詳しくは、こちらを見て欲しい。

Hilbert の講演の内、「数学の問題」と並んで有名なのが、1930年に彼の故郷ケーニヒスベルクで行われた "Naturerkennen und Logik", 「自然認識と論理」という講演である[Hilbert1930a]。この講演が有名なのは、その内容ではなく、講演の最後に、彼の墓碑銘でもある "Wir müssen wissen. Wir werden wissen."(画像)「我々は知らねばならない。我々は知るであろう。」という言葉が発せられたからだ。

この言葉は非常に有名で、Hilbert について語る時には、かならずと言って良いほど引用される。 この講演のショートバージョンは録音されてラジオ放送されたので、"Naturererkennen und Logik" で検索すると、色々と動画が見つかる。たとえば、Philosopy Overdose という YouTube アカウントの動画が、こちらで、最後の "Wir müssen wissen. Wir werden wissen." の部分が、こちらである。

これは 「数学のすべての問題はいつか解ける」という数学者の多くが持っていると思える信念の表明である。これと同じ意味のことを、 Hilbert が最初に語ったのは、実は1900年の「数学の問題」の中であった。この講演の中で、Hilbert は、数学者は全ての問題は解決可能だと信じていると主張したばかりか、「全ての問題は解決可能だ」という命題を「可解性の公理」 Axiom von Lösbarkeit とさえ呼んだのである。多くの数学者は、これを「数学者諸君、全ての数学の問題は可解である。それは約束されている。私の23の問題を解きたまえ！」という鼓舞のためのスローガンだと捉えた。

しかし、Hilbert の真の意図は異なり、彼はそれを本当に数学的に証明しようと考えていたのである。そして、1930年の講演の時期、彼は、長年の夢であった、それを実行に移そうとしていた。1920年代から30年代最初にかけての彼の数学基礎論研究の目的の一つであった数学の形式系の完全性証明である。そして、数学の完全性を示す証明を実行することこそが、彼の数学基礎論への興味の元々の動機だったのである。

これは、現代の我々の感覚からは信じられないことだが、史料が示すところによると、そう解釈することが最も自然だ。また、Hilbert は、そういう人だったのである。あるいは、そういう時代だったと言っても良い。実際、そういう哲学まがいの問題から距離を置くようになった Bourbaki 世代の中にさえ、André Weil から数論での活躍を期待されながらも、若くして亡くなってしまった Jacques Herbrand の様に、常々「完全な数学の理論を作りたい」と最も近しい友人 Claude Chevalley に語っていた人さえいたのであるから。

この「数学の可解性」への信念と、それを証明しようとした動機は、一見、このテキストの対象である不変式論研究とは無縁の様に思われる。私は、20年程前に行った彼の数学ノートブックの研究から、そこに何らかの関係はあるだろうと思ってはいたが、それほど深い関係ではないだろうと考えていた。また、それについて書いた岩波文庫の「不完全性定理」の解説も、その様な観点から書いた。

彼の数学基礎論研究の主たる動機としては、やはり、集合論の矛盾という数学の危機に際して、数学を救うために行った研究だったというのが、数学のリーダーに相応しいと思っていた。不変式論研究の時代に、"Wir müssen wissen. Wir werden wissen" に当たるものが、すでにあったことを示す史料を発見してはいたが、何か哲学的な思索が背景にあるのだろうと位に思っていた。

しかし、今回の東大講義のための不変式論史研究の結果、実は、有限基底定理の証明方法への Gordan による批判が、すべての始まりであると思われる証拠を幾つか発見した。これはある意味でアンチ・クライマックスで、数学基礎論研究の主たる動機が、数学を危機から救うためという、Hilbert の数学のリーダーとしての責任感から、駆け出しの若い数学者が当時の大家から受けた批判への反論のためへと変ってしまうのである。

しかし、史料が語るところからすると、そうとしか思えない。ただ、この事を説明するには、私が20年程前に行い、未だ公表していない Hilbert 数学ノートブック研究の内容などが必要となるので、このテキストで、その詳細を説明することはできない。しかし、その概要は4章で説明する。

さて、Hilbert という人物の紹介は、この程度に留め、最後に、彼が愛してやまなかったと言う生地 Königsberg ケーニヒスベルクについて、一言述べたい。彼の数学ノート第一冊の冒頭には、この街への愛を象徴すると思われる、ケーニヒスベルクでのバラ色の日々についての詩の様なものが記されている。

日本で言えば鎌倉に例えるのが恐らく一番適当な、このドイツの古都は、第2次世界大戦末期の英空軍の爆撃と、独ソ両軍の間の地上戦、その後のソ連による徹底的な破壊により、現在は存在しない。林が調べた範囲では、ケーニヒスベルク時代からの建築物で、現在も存在しているものは哲学者カントの墓所でもあり、冷戦終結までは、瓦礫と呼ぶ方が適当ではないかと思われる程の廃墟として放置され、その後修復されたケーニヒスベルク大聖堂を含めても三つだけである。

この街の破壊は実に徹底していて、Hilbert の生家の位置を特定しようと試みたが、街路自体が完全に変わっていて出来なかった。この古都は、その住民が話していた低地プロイセン語というドイツ語方言とともに、この地上から、ほぼ完全に姿を消したのである。

しかし、ドイツ人にとって、この街は、今でも郷愁を呼び起こすものらしく、それについての書籍や地図、当時の映像を収めたDVDなどが刊行されている。低地プロイセン語も、先ほど述べた Hilbert 自身による1930年の「自然認識と論理」のラジオ局での再現録音などで聞くことができる。

私は、Hilbert 研究を通して、この幻の古都に興味を持つようになり、それに関する DVD や書籍、地図などをかなり集めているので、 東大の講義では、それらを見せながら、この街について、また、北方十字軍に由来する、この街の歴史について、さらには、それが象徴しているヨーロッパの複雑な歴史について詳しく話す予定でいた。しかし、Hilbert 不変式論史の定説の崩壊のため、時間の関係で、この一番楽しみにしていた事が出来なくなった。これは残念であった。何かの機会に、やってみたいところだ。

ちなみに、現在、このドイツの古都の瓦礫の上に建っている軍港都市こそ、ウクライナ戦争のために日本でも一部では知られるようになった、バルト海に面するロシアの飛地カリーニングラードである。

2．Hilbert 不変式論と有限基底定理

ここから Hilbert 不変式論の歴史について見ていくが、講義で話す予定であった定説が、その講義の準備作業を通して崩れてしまうという異例の事態を受けて、東大における講義の歴史叙述は異例の形になった。そして、その講義資料に基づいている、このテキストも同じく異例なものにならざるを得ない。淡々と通史を語るということが出来ない。定説が大きく崩れたのは一点のみ、有限基底定理の発見譚においてのみである。そこに解説を集中せざるを得ない。

定説の崩壊は、 Hilbert が何時有限基底定理を発見したのかということについての従来の常識において起きた。現実は従来の常識より早かったのである。しかし、この発見時期の変更は、それだけに留まらず、どういう問題意識で、それが考え出されたのかということの常識にも疑問を突きつけることになった。そして、それを考察していくと、最初の非構成的な現代代数学の定理と見なされることが多い有限基底定理のルーツが、矛盾的なことに、非構成的な現代代数学の対極として語られる Kronecker の代数的整数論であった可能性が浮上して来たのである。これについては、東大講義の時点では、史料による確定的な証拠を見出せないままだったが、その後の研究で、ほぼ確定的といえる史料を、1889年から90年の冬学期の代数構造についての講義録で見つけることができたので、現在では、まず間違いないと思っている。

ただし、これには、もう一つ別のルーツがあった可能性がある。Gordan によるディオファントス連立方程式の解に関する「Gordan の補題」と呼ばれているもののオリジナル論文での証明の仕方である。実は、Gordan の証明では、現在の言葉でDickson の補題と呼ばれている命題が直観的に正しいかの様に書かれていて、 その後、Dickson の補題が、その存在を保証するディオファントス方程式の特殊な解の有限集合を、具体的に計算するアルゴリズムを Gordan は書いている。

これは飽くまでひとつの可能性に過ぎず、史料的証拠はないのだが、Hilbert が Kronecker の代数的整数論の枠組みの中で、有限基底定理を発想できたのは、この Gordan の証明方法を、Gordan との議論の中で知ったからではないかと思うのである。それを証明する史料はないが、それをサポートする、あるいは、私に、そう思わせる史料は3章で提示することになる。それは、Königsberg における不変式論講義の講義録である。

そして、この有限基底定理のルーツの問題以外にも、再考せねばならない重大な問題が浮上してくる。 つまり、発見時期の同定の変更という小さな歴史認識の変更が、従来の常識を次々に崩してしまうのである。そして、その最初の小さな変更を迫るのは、従来から良く知られていた、Hilbert の Felix Klein 宛ての二つの書簡の二つのフレーズなのである。しかも、その書簡の一つは、私が勝手に「神学騒動」と呼んでいる数学者間の騒動における、Klein の対処が、ホンの少し違えば、おそらく書かれなかったであろうものなのである。

もし、この二つの書簡が両方とも書かれていなかったら、おそらくは真実は歴史の闇に沈んだままで、永久に明らかになることはなかっただろう。Klein の対応が違って、二番目に書かれた書簡が書かれなかったとしたら、歴史家は永遠に最初の書簡が突き付ける奇妙な問題を解明できなかったかもしれない。しかし、幸い、偶然のお陰で残された史料で、我々は真実を知ることができるのである。この様な事を、3,4章を通して明らかにしていくのが、これ以後の目的となる。

3章では、新説の主に数学的側面に焦点を当て、4章では、神学騒動に焦点を当てる。3章の方では、大幅に従来の定説の常識を書き直すことになる。一方、4章では、その騒動の詳細を、従来知られていなかった数学者間の書簡の分析により明らかにすることにより、少しの訂正は必要であるものの、概ね従来の定説を踏襲し、またその根拠を強化することになる。

数学では証明ができれば、それは真実となる。しかし、歴史学では、複数の対立する説が競い合い、それらの中で、より合理的なものが定説となっていく。そのため、新説を提示しただけでは、不十分で、それを従来の説、そして、もう一つ出されている MaLarty の異説と比較するということが不可欠である。歴史学における「真理」は、証明ではなく、弁証法的過程によって生まれるのである。そのため、この2章では、3、4章と対比させるための、定説と、McLarty のそれへの異説を紹介する。そして、その上で、私の新説を紹介する。

上で、4章では従来の説を強化すると書いたが、従来語られていてことが全部正しいということではない。たとえば、Cayley が有限基底定理に a priori な困難を覚えたという Reid の説は、東大講義でも史料を使って否定したが、同様に否定すべきことはある。例えば、東大講義の後に、その存在に気が付いた[Rowe2018]は、定説の最終形態と言えると思うが、McLarty の説を一部で取り入れているため、その元となったた[Rowe2005]よりかえって悪くなっている部分があり、そういう部分は否定することになる。

では、全体的な説明は、これで終り、早速、具体的話に移ろう。まずは、すべての背景知識となる、有限基底定理というものの、簡単な数学的解説から始める。ポピュラー数学史ならば、これを省略というより、避けるわけだが、これは東京大学数学における数学史の講義に基づくWeb文書なので、まずは 殆どの人たちには理解不可能な正確な数学的知識を持って、その上で歴史を見るわけである。そうでないと、例えば上に書いた Reid の誤りの訂正ができない。

ちなみに、東大講義では、登録者、レポートの提出者ともに、院生の数の方が学部学生の数より多かった。学部学生でも非常に良い成績の人もいたが、数学的内容が強い問題の解答の質では、院生の解答の方が学部生のそれを遥かに凌駕していた。そのレポートの採点を通して、東大の数学の院生位の数学上の理解力がないと、こういう所謂「現代数学の歴史」を本当に理解するのは困難なのだと思ったものである。そして、このテキストは、そういうレベルの読者を想定して書いている。

2.1. 有限基底定理による Gordan 問題(Cayley の予想)の解決

Hilbert の不変式論研究について、最も広く知られているのが、不変式の「有限性」についての Cayley の予想の解決だろう。これは、Gordan問題の解決と呼ばれることが多いが、既に述べた様に、これは本来 Cayley が[Cayley1856]で予想したものである。

しかし、Cayley は、その後自身の予想を疑うようになり、また、その binary の場合を、ドイツの数学者 Paul Gordan が[Gordan1868]で解決し、その後、3変数以上の場合の解決が、当時の数学の大きな問題として残ったために Gordan問題と呼ばれるようになったようである。

つまりは、次の問題である。

Beweis, dass jede Covariante und Invariante einer binären Form eine ganze Function mit numerischen Coefficienten einer endlichen Anzahl solcher Forｍen ist.

Proof that every covariant and invariant of a binary form is an integral function with numerical coefficients of a finite number of such forms.

そして、この問題を3変数以上の場合に解決したのが Hilbert の1890年の論文[Hilbert1890]で、1章で述べた様に、この論文では Hilbert は不変式に対してだけ Cayley の予想を証明したのである。これは彼の最初の大きな数学的業績だった。そして、この Gordan 問題の解決を数学史上の一大発見としたのが、問題自体の解決より、それに使われた有限基底定理だった。

2.1.1 Hilbert の有限基底定理のオリジナル版

Hilbert の有限基底定理は、現在の言葉で言えば、「ネーター環を係数とする多項式環はネーター環である」あるいは「体を係数とする多変数多項式環はネーター環である」となるが、Hilbert 自身の有限基底定理は、次の様な定理であった。

1章の不変式論の概念を理解できた読者には明らかだろうが、この定理は不変式論との直接の繋がりはない。詳しい話は3章で解説することになるが、Gordan 問題解決のために書かれた論文として説明されることが多い論文[Hilbert1890]は、実は不変式論の論文としては書かれていない。それは、IからVまでの5つのセクションに分かれていたが、その内のIからIVまでで、不変式論の用語が出てくるのは、一回だけで、それも冒頭の目次のセクションVの題名としてだけなのである。

しかも、その応用のセクションVで使われるのは、セクションIの Theorem I のみで、他のセクションの結果や概念はVの Gordan 問題の解決の証明には全く使われていない。つまり、この論文は、代数形式 algebraic forms の一般論についての論文なのであり、Gordan 問題の解決の Hilbert 自身による扱いは、彼の一般論の応用に過ぎなかったのである。もちろん、当時無名に近かった Hilbert を一躍有名にしたのは、その応用だったのではあるが。

2.1.2 Gordan 問題(Cayley の予想)の証明

細部の説明は3章で行うが、この有限基底定理を使って、Hilbert がどうやって Gordan 問題を証明したのか、その概略を説明しよう。幸いに、そういうことが出来るほど、Hilbert の証明はシンプルだったのである。

まず、不変式の列 \(\mathcal{I}_1, \mathcal{I}_2,\ldots\) で、それが不変式全体の基となるもの、つまり、他の不変式が、 Cayley の予想の様に、それらの有限個のものの多項式で書けるものを作る。これが出来ることは、例えば、変数の数と weight を指定すると、それを持つ不変式の全体は有限次元ベクトル空間になることや、第一基本定理により解る。

この式の列の最初の有限個の \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) で、列の他の要素 \(\mathcal{I}_i\) のすべてを、 その多項式 \(p(\mathcal{I}_1,\ldots,\mathcal{I}_m)\) として表せることができれば、列の要素だけでなく、すべての不変式が、やはり、その多項式で表せることは明らかであるから、それで Gordan 問題は解決されたことになる。

そして、実は、その様な \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) を作るには、\(\mathcal{I}_1, \mathcal{I}_2,\ldots\) に有限基底定理を適用するだけで良いのである。もちろん、その時、任意の要素 \(\mathcal{I}_i\) を表す「線形形式」 \[ \mathcal{I}_i=\mathcal{A_1}\mathcal{F}_1+\cdots +\mathcal{A_m}\mathcal{F}_m \] の係数 \(\mathcal{A_1},\ldots,\mathcal{A_m}\) は不変式でさえない。しかし、Hilbert は、これを段々と「不変式化」して、最終的に、 \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) の多項式で置き換えられることを示したのである。

そのために、彼は Cayley の \(\Omega\)-process とよく似た式の変形方法を定義した。仮にそれを、Hilbert の頭文字で H-process と呼ぼう。この H-process は、ある強い意味で「線形」に作用し、また、任意の form を不変式に変形できた。しかも、\(\mathcal{I}\) が不変式ならば、有理数 \(c\) を適当に取って、\(c\mathcal{I}\) に対して H-process を適用すると、結果が元の不変式 \(\mathcal{I}\) になるようにできた。

そこで、\(c\) が、\(c\mathcal{I}_i\) を H-process 適用後に \(\mathcal{I}_i\) に戻すような有理数だとして、それを \[ \mathcal{I}_i=\mathcal{A}_1\mathcal{I}_1+\cdots +\mathcal{A_m}\mathcal{I}_m \] の両辺に掛けた上で、H-process を適用すると、上に説明した「強い線形性」などの性質から、それは次の様な形になる。 \[\tag{1} \mathcal{I}_i=\mathcal{J}_1\mathcal{I}_1+\cdots +\mathcal{J_m}\mathcal{I}_m \] ただし、\(\mathcal{J}_i\) は不変式である。 これらの不変式 \(\mathcal{J}_1,\ldots,\mathcal{J_m}\) が \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) の多項式として表せれば、問題は解決されたことになる。

つまり、H-process により、「\(\mathcal{I}_i\) を \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) の多項式として表す」という問題が、より小さい次数の \(\mathcal{J}_1,\ldots,\mathcal{J_m}\) のそれぞれを、 \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) の多項式として表すという問題に還元された。従って、以上の議論を繰り返すことにより、 やがては、 \(\mathcal{J}_1,\ldots,\mathcal{J_m}\) は定数になり、そうなったとき、 \(\mathcal{I}_i\) は、最終的に \(\mathcal{I}_1,\ldots,\mathcal{I}_m\) の多項式となるのである。

ちなみに「強い線形性」の意味など、もう少し詳しく正確な話は3章で行う。また、「強い線形性」というのは、林の造語であるが、\(\mathcal{A_i}\) がスカラでないため、本当は線形形式ではない、\(\mathcal{A_1}\mathcal{F}_1+\cdots +\mathcal{A_m}\mathcal{F}_m\) を「線形形式」と呼ぶのは Kronecker や Hilbert が行っていることである。

では、数学的予備知識が出来たので、歴史の話に入ろう。それは、有限基底理定理の発見と、それを巡る騒動である神学騒動の話である。

2.2．有限基底定理が引き起こした神学騒動

19世紀後半から20世紀前半の数学の歴史は、数学の長い歴史の中でも特に特異である。Riemann と Dedekind という Göttingen 大学の二人の友人の数学を契機として、集合を用い計算より論理的思考を重視する概念的数学が誕生し、それが数学の主流になるという大変革が起きたからである。

ドイツの小さな古い大学街の二人の若い友人たちにより、数学という古く大きな研究分野のスタイルが、全くと言って良いほど変わってしまったのだから、実に驚くべきことである。では、この二人が引き起こした変革とは何だったかと言うと、式と計算中心の数学が、集合を使う概念と論理の数学に変貌したことである。

読者の中には、高校数学から大学の数学に移行する際に違和感を感じた人がいるかもしれない。高校までの数学、特に証明が、Hilbert の時代に起きた大変革前の証明で、大学の数学科で学ぶ証明が、それ以後の証明だと思えばよい。3章で、Gordan の補題と呼ばれている、線形連立方程式の整数解に関する定理を紹介するが、 それの[Gordan1885]での Gordan の証明は高校数学のそれにそっくりである。今の大学の数学科で、それをテストやレポートに書いたら、きっとバツがつく。この変化が、この二人が起こした革命の結果なのである。

ただ、その革命は数学の分野において起きた時期にずれがあった。それを代数、しかも、一般代数の分野で最初に起こしたのが、有限基底定理だとみなされているのである。そして、古いスタイルで代数学を行っていた Gordan が、Hilbert の有限基底定理の証明を、数学のまともな証明と認めなかったというのが神学騒動なのである。

私が、それを「神学騒動」と呼ぶ理由は、ドイツの代表的な数学雑誌の一つ Mathematische Annalen に投稿された[Hilbert1890]の原稿に対して Gordan が

Das is nicht Mathematik, das is Theologie.

"That is not mathematics, that is theology."　「あれは数学じゃない、神学だ」

当時のドイツ代数学の研究者の中には、今までの不変式論の解説で行った様な式計算による数学を第一級の数学と見做し、複素数の連続性を必要とする代数学の基本定理さえも、二級の数学、あるいは、「超越的」と考える人達が一定数いた。その代表と言うべき人が Kronecker であったが、Gordan もそういう一人であったようだ。

Gordan の不変式論講義[Gordan1885]の第12節は代数学の基本定理に当てられているが、その最初の項は、"Transcendeter Theil des Beweis", 「証明の超越的部分」とタイトルされていて、本文でも「超越」という言葉が2度も繰り返され、「ここから、実数係数の代数方程式が実根を持つという前提のもと、超越的領域を去って純粋に代数的に話を進めることができる」という意味のことが書かれている。要するに中間値の定理を使ったことに、何か後ろめたいことがあるかの様な書き方なのである。現代からすると理解し難いセンスだろう。その部分に対応する目次の画像を示しておく。

ちなみに、Kronecker は、もっと凄くて、彼の代数学の基本定理は、方程式の Galois resolvent を求めるアルゴリズムと、その resolvent から各根を求める近似計算の組み合わせだった。各根の値を近似的に計算する方法は、普通に積分を使って説明されている。おそらく、resolvent の計算までが一流の数学、あるいは真に純粋な数学で、そこから後は二流の数学なので、数学的に純粋でないと彼が見做した解析学も使って良いというのだろう。

しかし、Hilbert の有限基底定理は、本質的に non-constructive な組み合わせ論に基づいていて、Kronecker や Gordan が重視した「式計算のアルゴリスミックな操作だけを使用する代数学」の範囲で理解することはできない。そのため、Gordan には、Hilbert の証明が、数学の正統な道を、少なくとも彼が信じる不変式論研究の正統な道を踏み外している様に見えたのだろう。そして、Gordan は、その事を根拠に、Hilbert の論文の Math. Annalen での掲載にさえ反対さえしたのである。それに Hilbert が激しく反発した。それが神学騒動である。

数学における集合が当たりまえになっている現在からは、むしろ古臭く見える方法で定式化された Hilbert の有限基底定理であるが、当時の認識は違った。例えば、当時、設立されたばかりのドイツ数学会の機関誌は、主要な分野の総合報告を掲載することなっており、Hilbert の主要な業績の一つとされる、Dedekind のイデアル論を用いて、Kummer, Kronecker などの代数的整数論の理論の多くを再編してみせた、所謂、数論報告 Zahlbericht も、その一つだった。つまり、総合報告が、報告すべき理論を書き変えてしまったわけである。果たして、そういうのを総合報告というのだろうか。Hilbert が如何に強引な人だったかが解るエピソードである。

そして、そういう総合報告の不変式論版であり、また、その総合報告シリーズの最初のもので、1892年に出版された同学会の年報第1号(1890/1年)に掲載された Franz Meyer による[Meyer1892]では、Hilbert の不変式論における業績が、最近の優れた仕事として、色々と紹介されながらも、この有限基底定理による Gordan 問題の解決に言及した時には、それが Cantor が実数を定義するのに使ったのと同じ様な議論を使っていること、また、Wissenschaft(科学、学)からは、無限のプロセスを放逐すべきだという意見もあるとコメントされている。[Meyer1892],p.144,2番目の脚注の最後の文で、原文が "Allerdings giebt es eine Richtung in der Wissenschaft, die derartige unendliche Processe überhaupt verwirft." Gooble translate の訳が、"However, there is a trend in science that rejects such infinite processes altogether" である。

何が問題だったかというと、「form の任意の無限列」であった。Cantor の議論というのは、我々に取っては当たり前の実数の定義のための基本列、つまり、有理数のコーシー列のことである。そういうものに違和感を抱くということが、我々には違和感の元だが、時代が変われば考え方も変わる。当時のドイツの数学者の一部の人たちに取って、それはまるで「数学に哲学を持ち込む行為」の様に見えたのだろう。そういう人たち、例えば､Kronecker, おそらくは、Gordan に取って、数学は哲学の一部の様に形而上のものでは無く、「任意の無限列」などという概念は、哲学者がもてあそぶ数学的立場からは不合理なもの、あるいは超越的なものに見えたと思われる。無限列は式などにより、具体的に示された時のみ意味を持つ、この人たちは、そう考えたようだ。

この様な Hilbert の有限基底定理に対する Gordan の批判の言葉を最初に報告した文書は、彼の Erlangen 大学での同僚だった Max Noether による Gordan の追悼記事 "Paul Gordan",[Noether1914]だと思われるが、アメリカの哲学者 Colin McLarty が[McLarty2012]で指摘するまで、この事は忘れられていたものと思われる。

McLarty は、この Gordan の発言があったという Noether の記述の根拠が不明とし、実は、Gordan は Hilbert の証明方法に対して、全く批判的ではなく、また、「神学云々」という発言も無かったという説を主張している。しかし、これが歴史学的には如何に無理のある説であるかということは、この2章と、主には、4章で、この神学騒動の最も深い当事者が、Klein であり、この Gordan の発言は、その Klein が Noether に伝えた可能性が非常に高いことを示す史料を提示することにより実証することになる。

その Klein は、第一世界大戦中から1919年にかけて Göttingen の彼の自宅で行われ、彼の死後の 1926 年に出版された19世紀数学史講義[Klein1926]の中で、この「神学騒動」について、Noether より詳しく語っている。つまり、McLarty の説を反駁するには、Klein から Noether に情報が伝わった事、Klein の講義での発言の信憑性が高いことを実証できれば良いことになる。前者は、この2章で、後者は4章で実証していく。

神学騒動は、長らく数学者の世界だけで知られていたものと思われる。Klein の数学史講義は、明らかに数学者や数学の学生に向けられたもので、数学者の中でも、それに盛り込まれた数学を全部理解できる人など希だったと思われるからである。

そういう、神学騒動と、Gordan の発言が、数学者の世界を超えて広く知られる様になったのは、Constance Reid による Hilbert の伝記、"Hilbert" [Reid1970]によってであったろう。Reid は、Klein の歴史講義の内容などを元に、その著のV章"Gordan's Problem" で、アルキサンダー大王に関する古代の「ゴルディオスの結び目」、英語で、Gordian Knot の伝説に絡めて、神学騒動と、Hilbert の有限基底定理の革新性を生き生きと描き出して見せた。そして、この Reid による「物語」により、Hilbert の神学騒動が、数学者にも、数学愛好家にも、そして私の様な歴史家にも理解されていたと言えるだろう。

Reid は、その著書で、Hilbert の証明の「神学的超越性」を、すんなり受け入れたのは、Klein だけだったと主張し、その証拠を幾つか挙げている。たとえば、Hilbert は、その1890年の論文の前に、Göttingen 紀要(正式名は、Abhandlungen der Königlichen Gesellschaft der Wissenschaften in Göttingen) に、その内容を速報する三つのレポートを投稿しているが、その offprint を受け取った Cayley が、その様な証明が出来たということにアプリオリな疑問を感じるという返信を Hilbert に書き送っていることを挙げている。 しかし、この2章で、明らかにするように、実は、Cayley がアプロオリな違和感を感じたのは、有限基底定理ではなく、Hilbert の H-process の使い方の方だったのである。Cayley は、有限基底定理に何らの違和感も感じなかったらしいことは、史料に基づいて議論可能である。

これから、この様な話を、3,4章 で史料画像を見せながら詳しくしていくことになるのだが、この2章では、私の新説に対比させるための旧説と、それに対する McLartyの異説の解説を主に行う。ただし、その中で、さきほどの Cayley の書簡への Reid の誤解のように、簡単に修正できるものは、この2章で修正を行う。そして、そういう単純な話では済まない修正を、主に3章で行うことになる。では、まず、定説、従来までの、Hilbert の有限基底理定理と神学騒動に対する歴史認識がどんなものだったのかを見て行こう。

2.3. Hilbert 不変式論についての「定説」

ここで従来、Hilbert の不変式論研究について、どの様な歴史学的言説が成されて来たかを、その言説を引用しながら説明する。ちなみに、Hilbert の不変式論研究についての、まとまったアカデミックな数学史研究というものは探して見たが、意外なことに見つからなかった。おそらくは、東大講義のために行った私の研究が最初のものだろうと思う。

林は20年ほど前に、Hilbert の Königsberg での不変式論講義の講義録などを調べてはいたが、それは不変式論史のためではなく、その時期の Hilbert の数学思想を、そういう史料の中に見るためだった。その頃、不変式論史と言えるものが無いのは知っていたが、今回、また調べてみて、この20年間にも、そういう研究は無いようだったのである。

その一方で、神学騒動は大変有名で、林が岩波文庫の不完全性定理の解説の中で書いた様な短い言及は、あちこちで見かける。その内、おそらく、最も古いと思われる二つの言及と、他の多くの言及のソースとなっていると思われるものを三つ、そして、その三つをソースとして書かれたと思う私の岩波文庫の解説を含む幾つかの言及を紹介し、最後に、「定説の完成形」というべき[Rowe2018]の内容を説明する。ちなみに、この[Rowe2018]の存在には、東大講義の後に気が付いたので、東大講義では、これについての言及を行えなかった。

これらの歴史解説の内、最も古い Max Noether と Klein のもの以外には、私のものを含めて間違いがある。史料を使えば、それらが間違いであることは簡単に分かるので、ここでそれらを史料の画像を示しつつ指摘する。そして、次の3章以後で、その間違いを、どの様に修正して歴史を書き直すべきかを説明することになる。

2.3.1. Max Noether の言及

ネーター環の Emmy Noether の父で、Hilbert の零点定理 Nullstellensatzの元となったAF+BG定理で知られる、Max Noether は、Erlangen 大学で Gordan と長く同僚だった人で、1912年に Gordan が亡くなった後、1914年に Mathematische Annalen に追悼記事[Noether1914]を書いたのは彼だった。

この追悼記事で、Noether は、Hilbert の Gordan 問題の解決を詳しく説明した後、Gordan の有限基底理への反応を次の様に書いた([Noether1914],p.18)。

Gordan - anfänglich diesen begrifflichen Deduktionen gegenüber mehr ablehnend: „das ist keine Mathematik, das ist Theologie!" - ist dann zweimal (53), (69) dem diesem Beweise zugrunde liegenden Hilbertschen Endlichkeitssatze nähergetreten, indem er die gegebenen Formen \(F\) nach verschiedenen Kriterien in eine Reihe anordnete, die das Bilden eines endlichen Moduls aus ihnen deutlich machte; das erstemal in komplizierterer Weise speziell für die Invariantenformen, das zweitemal allgemein und einfach.

Gordan - initially more opposed to these conceptual deductions: "This is not mathematics, this is theology!" - then twice (53), (69) approached Hilbert's finiteness theorem, which is the basis of this proof, by arranging the given forms \(F\) in a series according to various criteria, which made it clear that a finite module could be formed from them; the first time in a more complicated way, specifically for the invariant forms, the second time in a general and simple way.

当初は(林補足：Hilbert による Gordan 問題解決に使われた)概念的演繹に反対し、「それは数学ではない、神学だ!」とさえ否定した Gordan だったが、後に2度、(53)と(69)で、与えられた form \(F\) の列を、様々な条件により並べ直すことにより、(林補足：Gordan 問題の)この証明の基礎であった Hilbert の有限性定理にアプローチし、それにより、有限の Modul の構築が可能であることをクリアにした。最初の(53)では、それは不変式に対してだけ複雑な条件を使って行われ、2度目には、一般的な場合にシンプルな方法で行われた。

(53),(69)というのは、このWeb文書の文献・史料表の、それぞれ[Gordan1893],[Gordan1899]の事である。 Noether は、これらにより有限基底定理がクリアになったと言っているが、私には[Gordan1893]の方はそうは思えない。

その一方で、[Gordan1899]の証明は、大変優れたもので、n個の自然数からなる tuple についての組み合わせ論的補題で、現在、Dickson の補題と呼ばれているものの単項式版を使い、有限基底定理の non-constructive な組み合わせ論的本質を白日の下に晒すものである。つまり、これについては Noether の説明通りであり、また、その様なものなので、現代のモノグラフや教科書、たとえば、[Kung&Rota1984],[Sturmfels2008]では、Hilbert の証明ではなく、Gordan の証明で有限基底定理を証明している。

この Max Noether による Gordan 追悼文が「最初、Gordan は、それは数学ではない、神学だ、と、Hilbert の証明を批判したが、後に、その『神学』を評価する様になった」という有名な逸話の初出と思われる。それは、次に説明する「Klein の言及」の数学史講義より数年前のことである。

しかしながら、時間的オーダーは確かに、こちらが先なのだが、「情報の流れ」という意味では、こちらの方が「川下」にあたると思われる。というのは、Noether は、「神学騒動」に関わった形跡が全く無い上に、その追悼記事の著者名の表示のすぐ下に、

(Mit Unterstützung von Felix Klein in Göttingen und von Emmy Noether in Erlangen.)*)

(With support from Felix Klein in Göttingen and Emmy Noether in Erlangen.)*)

*) Von Ersterem wurde ich in der Gesamtwürdigung, von Letzterer in der Würdigung der algebraischen Arbeiten wesentlich unterstützt.

*) I received significant support from the former in the overall assessment, and from the latter in the assessment of the algebraic work.

次の画像 Img-2 で、その注釈と脚注を示す。

この Klein のサポートが郵送によるものならば、Klein から Noether への書簡に、その証拠があるのではないかと調べてみたが、Göttingen 図書館の Klein Nachlass の Noether からの書簡群には、1900年以後のものが残念ながら存在しなかった。恐らくは何かの理由で失われたのであろう。

しかし、逆に Noether が追悼記事執筆時に、Klein 宛に書いたと思われる "Erlangen, 29. Nov. 1913" と記された書簡が見つかり、その中に、

Von Deinen Anmerkungen habe ich so ziemlich Alles herübergenommen,

I have taken over pretty much everything from your comments,

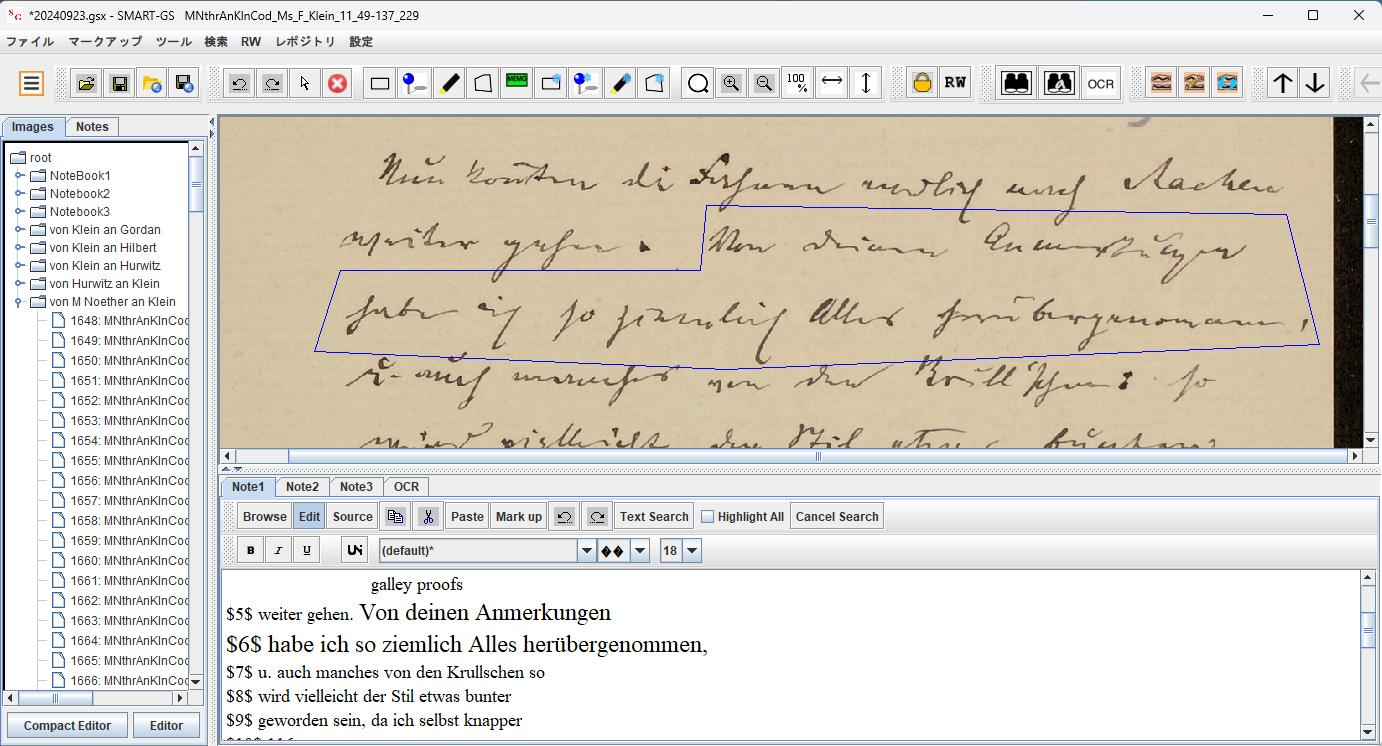
画像の全体を見るには、こちらのリンクから画像を新しいタブで開いて見ると良い。また、これは直ぐ後の2.1.1で説明する SMART-GS という手書史料分析ツールで、Noether の書簡を翻刻している所の画像だが、Noether の書簡の、該当ページだけの画像は、こちらで、該当分だけの画像が次の Img-4 となる。

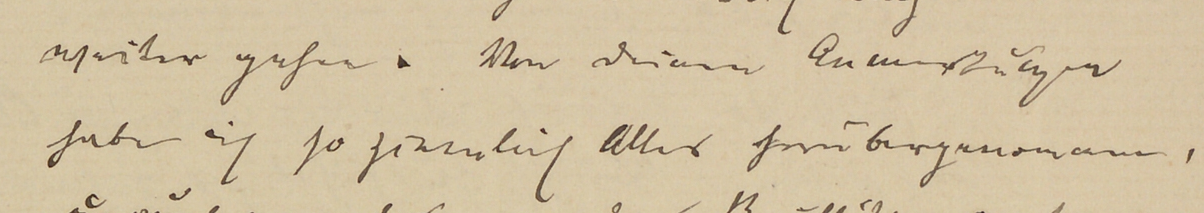
書簡自体は、Göttingen 大学の図書館、Niedersächsische Staats- und Universitätsbibliothek Göttingen が所有しており、上に示したものは、それを同大学の GDZ Göttinger Digitalisierungszentrum ゲッチンゲン・デジタル化センター で電子画像化され、Public Domain Mark 1.0 (PDM) のライセンスで一般公開されているものである(同史料のURL:https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3200061)。

これは、単に Noether の手紙の画像を示すだけの画像でなく、林が中心になって20年位前に開発を始めた手書き資料分析用のツール SMART-GS で Noether の手紙を翻刻している様子を見せるための画像になっている。この Max Noether から Klein への書簡を例として、林がどの様にして19世紀の書簡の翻刻・分析を行っているかを説明する。これが、林の新説の正しさの重要な証拠になる。そこで、ここで、実際にどうやって翻刻しているかを説明しよう。

2.3.2. 翻刻に使っている IT ツールとサービスとそれを使用した翻刻の実際

ドイツ語の筆記体は大きく分けて、(i)中世から使われており、ドイツ文字とか亀の子文字と呼ばれる Fraktur の筆記体である Kurrnetschrift クレントシュリフト と、(ii) 現在も使われており、基本的に英語の筆記体と同じ Normalschrift ノルマルシュリフト に大別されるが、Kurrnetschrift には、1910年代に政府により作られた Sütterlinschrift ジュタリンシュリフト というものがあり、これは Normal と Kurrnet の中間で、どちらかというと　Normal に近いものである。

このWeb文書で検討する書簡は、Gordan(1837生), Max Noether(1844生), Klein(1849生), Hurwitz(1859生), Hilbert(1862生)により書かれているが、Gordan は Kurrnet, Noether が Normal 寄りの Sütterlin, 他の三人が Normal を使っている。Normal は基本的に、現代人でも読めるが、Kurrent, Sütterlin は訓練を受けていない人には読めない。これは日本の古文書を読むためには訓練が必要であるのと同じことである。

現在、日本でもドイツでも、AI を使って、これらの古い手書きを自動で読み取る研究が進んでおり、特にドイツでは、既に Transkuribus.de という商用サービスが始まっており、林も、Gordan, Noether の書簡を読むためには、これを使っている(そういうものが登場する以前には、翻刻を仕事にしている米国人に依頼して Gordan の書簡を読んでもらったりしていた)。

この Transkribus.de で、Img-4 の部分は、次の様に翻刻された(使用モデル The German Giant I)。

Von Deinen Anmirtulgen habe ich so ziemlich Alles hern bergenomam!

難題は、herübergenommen であった。最後が genommen であろうことは、容易に分かるのだが、語頭から、そこまでで明瞭なのは、h と b, そして、b と g の間に e があるだけで、非常に読みづらかった。また、Transkuribus.de が二語と読んだ hern と bergenomam の間には、まるで二語を繋ぐというような記号の様なものが書かれており、これが謎だった。

こういう時には、大雑把に推測して作った候補を辞書ではなく、Google books で19世紀の書籍に限定してサーチするという方法などが有効で、現在は使われていない単語なども、それにより見つかるし、用法も分かる。Google books の19世紀の書籍の集積は素晴らしく、世界中の図書館の古書にアクセスしているようなもので、それがサーチもできるわけである。ただし、その Google books の翻刻が時に、間違えていることがあるので、ドイツ語などの知識でそれを補正することが必要である。

Transkuribus.de が hern bergenomam と読んだ部分は、1か月近く読めず、何度もトライしたが、Google translate に候補を示させる方法を使っていたとき、Herberge hostel という候補が見つかり、herbergenommen という候補を Goole books でサーチしたら19世紀を中心に多くのヒットがあった。しかし、元の史料を見ると、これは Goole books の誤翻刻で、本当は、herübergenommen であることが分かった。鍵括弧を倒した様な変な記号は、ü のウームラウトの二つの点のつもりだったのである。確かに、 Sütterlin では、ウムラウトの2つの点を繋いで書くことがあるようだ。しかし、今迄林が見た範囲で Noether がウムラウトの点を続けて書いた例は他には一つもないし、筆運びが全く異なるので書き損じたと言うべきだろう。ちなみに、筆運びは翻刻の際の重要な判断材料で、形は極端に崩れていても筆運びが同じ場合は、その文字を書く意図があったと判断することが多い。いずれにせよ、偶然に助けられて、これで漸く翻刻ができたわけである。

Img-3 で見せているエディタの様なツールは、林が20年近く前に Hilbert の数学ノート研究のために発案して、学生やボランティア、あるいはソフトウェア製作会社に依頼して作成した SMART-GS という手書き史料翻刻用のツールである。最初は林はコードを書かなかったが、ある程度完成してから、林自身もコードを書くようになり、現在使っているもののコードの大半は、林の手が入っていたり、林が一から書いたものである。

Hilbert 研究のために作ったのだが、一応使える様になる前に、その時の林の Hilbert 研究が一応完成し、林の興味も他に移ってしまい、当時実質的に Hilbert 研究に使ったのは、零点定理にあたる allgemeine Noetherian Satz という文字列を探索し、それにより、あるノート(メモ)の記述時期を同定したことだけであった。

SMART-GS の大きな特徴の一つが、はこだて未来大学の研究者が開発した、似た文字のパターンを画像探索するプログラムを搭載していることで、このプログラムの機能を利用したのである。これは難読文字列が別コンテキストで読めているときに非常に大きな翻刻の助けになる。

その後、このツールは、主に日本政治史、日本思想史などの大きなグループによる翻刻に使われ、世界最大の日記と言われる枢密院議長倉富勇三郎の日記の翻刻プロジェクトや、林による京都学派の哲学者田辺元の遺稿集研究プロジェクト、そして、西田幾多郎未公開ノート類の翻刻プロジェクトなどで使われてきたが、今回、15年以上を経て、初めて、開発動機だった Hilbert 研究のために本格的に使うことになったわけである。

これ以上の説明は控えるが、使用している様子のデモ動画を作っておいたので、興味がある方は見て欲しい。こちら(mkv版)とこちら(mp4版)である。いずれにせよ、この様な方法で翻刻しているので、その翻刻の精度も効率もツールを用いない場合に比べてはるかに高い。また、今回は林ひとりで翻刻を行っているが、これをグループで、例えば二人で同時に画面を見ながら、また、プロジェクタでPCの画面を投影して、10人ほどのグループで翻刻を行うと、驚くほど効率よく、また、高精度な翻刻ができることが知られている。

ちなみに、このグループによる翻刻の方法は京都大学名誉教授の永井和氏(現代史)の発案で、ペアで行う方法は西田幾多郎未公開ノート類の翻刻に携わった京大文学研究科ドイツ語学ドイツ文学専修の院生諸君の発案である。

さて、これで林が使っている翻刻の方法論の説明は終わり、「神学騒動の定説」の最大のソースとなったと思われる、Klein の言及に話を移す。

2.3.3. Klein の言及

数学者 Felix Klein は、Erlangen program などの多くの数学上の業績で知られるが、プロシアの有名な教育学術官僚 F. Althoff を通して大きな政治的力を持ち、それを使うなどして Göttingen に史上稀にみる数学の一大学派を形成した人である。そして、その影響力は、数学を越えて物理学にも及んでいたようである。

Klein は、数学教育、数学史などでも大きな貢献があった。数学教育については、大規模な国際会議の立ち上げや中等教育のカリキュラムへの影響が知られている。恐らく、これも Althoff との連携が大きかったのであろう。そして、数学史に関しては、第一世界大戦中(1914-1918)から1919年にかけて Göttingen の彼の自宅で行われ、彼の死後 1926 年に出版された19世紀数学史講義[Klein1926]が有名で、これは和訳もある。その中で、Klein が述べた「神学騒動」についての言及が、恐らくは、後に広く語られる様になる「神学騒動」の逸話の全ての始まりと言ってよいのだろう。

時間的には、これ以前に、先ほど紹介した、Max Noether による追悼記事があるわけだが、アメリカの哲学者 McLarty が指摘するまで、私は気が付かなかったし、寡聞にして、McLarty 以前に、それに言及したものを見たことがない。

Klein は、 Math. Annalen の編集者として、Hilbert の論文を扱った人であり、4章で明らかにするように、起きる必要がなかった「神学騒動」を、その意図に反して起こしてしまい、また、その火消しに当たった人で、騒動全体を知る唯一の人と言って良い。

Klein の19世紀数学史講義[Klein1926]は、アカデミックな数学史の講義であり、Klein の叙述は少なくとも我々が入手できる最も重要な情報源であり、後に見る書簡の内容とも整合性が高い。また、今回の林の研究を通して判断してみると、神学騒動の発端となった論文[Hilbert1890]の意味についての解説も、Klein の解説ほど正確で適切なものは他に無いように思う。

[Klein1926]のpp.329-331で、Klein は、Hilbert の有限基底定理が、Kroneckersche Ansätze mit Dedekindscher Denkweise, Kroneckerian approaches with Dedekindian thinking により、「すべての代数構造が有限個の代数方程式で記述できることを示すもの」として説明し、代数幾何学の新時代を開いたものであるとした。現代の代数幾何学で、代数集合が有限個の方程式で定義され、有限個で良い根拠として、有限基底定理があげられるが、Klein は、Hilbert の業績を、この事を通して説明したのである。

Klein は Hilbert が自身の論文でそうした様に、代数曲線の例を使って、この定理の意味を詳しく説明した後、それは不変式論への応用においても、eine glänzende Anwendung, a shiny application をもたらしたことを手短に説明した。実は、代数幾何学への応用の叙述は、不変式論への応用の2から3倍近くあり、明らかに前者の方に力が入っている。4章で明らかにする様に、不変式論の Gordan 問題の解決のための論文として語られることが多い[Hilbert1890]であるが、この Klein の書き方が如実に示すように、実は、そのタイトル Theorie der algebraischen Formen, Theory of the algebraic forms が語る如く、代数形式 form の一般理論についての論文なのである。そして、この2章の最後で指摘するように、そういう風に書かれたのは、Klein の示唆があった事が大きいと思われる。

短い不変式論への「輝かしい応用」についての Klein の言及の大半は、「神学騒動」に費やされていた。有限基底定理が、Gordan 問題の解決をもたらした事を説明した後、Klein は、「神学騒動」について、次の様に語っている([Klein1926], pp.330-331)。

Ihrer Eigenart entschprechend wurde diese Arbeit zunächst mit sehr verschiedene Stimmung aufgenommen. Mich hat sie damals bestimmt, Hilbert bei nächster Gelegenheit nach Göttingen zu ziehen. Gordan war anfangs ablehnend: "Das ist nicht Mathematik, das is Theologie." Später sagte er dann wohol: "Ich habe mich überzeugt, daß auch die Theologie ihre Vorzüge hat." In der Tat hat er den Beweis des Hilbertschen Grundtheorems selbst später sehr vereinfacht (Münchner Naturforscherversammlung 1899).

In its nature, this work was initially received with very different feelings. It made me decide to bring Hilbert to Göttingen at the next opportunity. Gordon was initially opposed to it: "This is not mathematics, this is theology." Later he said: "I have convinced myself that theology also has its advantages." In fact, he later simplified the proof of Hilbert's fundamental theorem considerably (Munich Natural Scientists Meeting 1899).

その特質故に、この研究成果は人により非常に異なった受け取られ方をした。私について言えば、この成果が、近い将来に機会を見て Hilbert を Göttigen に招聘する決心をさせたのである。Gordan は、最初、これに反感をもった：「これは数学ではない、神学だ」というのである。しかし、後に彼は「神学も役に立つと納得したよ」と言う様になった。実際、彼は、後にヒルベルトの基本定理の証明を非常に単純化する仕事をしているのである(Münchner Naturforscherversammlung 1899)。

この Klein の言及の最後の "Münchner Naturforscherversammlung 1899" という注釈については、面白い事実がある。この時代のドイツの論文には、その最後に完成させた場所で日付を書く習慣があったようなのだが、Noether による追悼文の文献(69)にあたる[Gordan1899]では、それが

München, September 1899.

この会議の記録を見てみると、Gordan は、"Über homogene Funktionen" という講演で、3章で紹介する「Gordan の第2補題」について話している。先ほどは、現代的な名称を使って紹介した「Dickson の補題」である。 [Gordan1899]は、Klein が "In fact, he later simplified the proof of Hilbert's fundamental theorem considerably" と言った、その当の論文で、「Gordan の第2補題」は、そのために使われた補題である。そして、それに Klein が質問して、Gordan が答えたと記録されている([GDNÄ1900], pp.28-29)。

この[Gordan1899]は、Göttingen 紀要で出版されたもので、そういう紀要論文は、協会で会員が報告した上で出版される。 おそらく、[Gordan1899]の原稿は、この時、Gordan から Klein に直接手渡し、Klein が報告し、そして、出版されたのだろう。その紀要論文は、有限基底定理の別証明を与える事を目的としているが、München の会議の講演は、そのための補題についてであったわけである。そして､それにも関わらず、Klein は紀要論文ではなく、Müchen の会議を引用している。これはいささか奇妙なことである。

"später" (後に) を2度繰り返し使った、Klein の書き方からすると、神学の有用性を納得したと言ったのは、これよりは前で、後で説明する Klein あるいは、Klein と Hurwitz による説得の際であったと考えるのが普通だと思う。しかし、"In der Tat" "indeed" と言っているので、ふたつの "später" は、同じ時を示していてもおかしくはない。そして、Klein が、自分自身が、それに報告した筈の、Göttingen 紀要ではなく、Münchner Naturforscherversammlung, Munich Natural Scientists Meeting を引用しているのは、この集会で、何らかの形で、Gordan から、有限基底定理の短い別証明と、「神学も役に立つと納得したよ」の発言を聞き、そのために Klein は、Göttingen Nachrichten の論文を引用するのではなく、"Münchner Naturforscherversammlung 1899" と引用したと考える方が自然であると思われる。

つまり、普通ならば、Gordan の短い有限基底定理の証明は、それが中心テーマでなかった、Gordan の München 会議での講演を表す "Münchner Naturforscherversammlung 1899" ではなく、自身が報告したであろう、Göttingen 紀要を意味する、"Göttinger Nachrichten 1899" などと参照する筈だろう。それが、わざわざ "Münchner Naturforscherversammlung 1899" としてあるのは、そこで Klein が、Gordan の「神学も役に立つと納得したよ」という発言を聞いことを示そうとしていたのであろうというのが私の現在の解釈である。

Gordan の第2補題は、[Hilbert1889a] で Hilbert が Gordan 問題の別証明のために使った Gordan 自身の論文[Gordan1873]における Gordan の直観を論理的に保証するものであった。 3章の2.4で説明する様に、そのことを考えると、この時点で、Gordan が「神学」の意味を強く支持する様になったということは、非常に自然なのである。

どちらが実際に起きたことなのか、今後の実証は難しいだろうが、我々の想像を掻き立てる話である。いずれにせよ、 Klein の数学史講義の後、Hilbert 自身が講演の中で、これについて語ったり、また、Hilbert への追悼記事で、これが引用されるようになる。しかし、それらは数学者をオーディエンスとしたものであった。この「騒動」を、そういう数学者の世界を越えて、広めたのが、次に紹介する Constance Reid による伝記 "Hilbert" であろう。

2.3.4. Reid の言及

神学騒動を、数学者の世界を越えて、有名にしたのは、1970年に初版が発刊された、アメリカの作家 Constance Reid による Hilbert の伝記[Reid1996]であるのはまず間違いないだろう。この著書は読者を魅了する読み物として大変優れたものだった。私の場合で言えば、特に印象的だったのは、"Gordan's Problem" というタイトルの第V章だった。Reid は、Hilbert の不変式論研究の時代を、Gordan 問題の解決を中心にして生き生きと描きだしていたからである。

神学騒動の核心部分の記述は、それが Klein に Hilbert の招聘を決意させたという記述があることから、Reid の第V章は、Klein の講義録を元に書かれていると思われるが、それ以外の多くの重要な情報が込められており、私には未だ、そのソースが分からないような情報も書かれている。Reid 氏には、一度、インタビューをさせていただいたことがあり、その際に、ご本人は、学者ではないと謙遜されていたが、明らかに並みの歴史家以上の綿密さと多大の努力による叙述である。

Reid の叙述の、Klein の講義との最大の違いは、有限基底定理の重要性を、代数幾何学の基礎への影響ではなく、不変式論の大きな未解決問題の解決に使われたという事の方に置いて語ったことだろう。というより、Reid の叙述では、有限基底定理というものが全く見えないのである。

実は、この著書には、数式がひとつも使われていない。もしかしたら、私の見落としがあり、一つくらいはあるのかもしれないが、見事なまでに数式を排除して書かれている。それでありながら、数学的に正確なのである。優れたジャーナリストとしての資質と、実妹が、Hilbert の1900年の23の問題の内の第10問題の否定的解決に最も貢献のあった Julia Robinson であったということが貢献しているのかもしれない。

Reid 氏へのインタビューでは、Hilbert の数学基礎論の時代の忠実な助手 Paul Bernays や、Hilbert 第10問題の最終的解決者のソ連の数学者 Yuri Matiyasevich との親密な交流など、多くの優れた特にユダヤ系の数学者たちとの交流について聞くことができた。そういう交流を通して、正確な情報が、Reid 氏に伝わっていたのだろう。

Reid の叙述により、有限基底定理から Gordan 問題の解決の方に重点が移行してしまった。これはある意味では仕方ない事でもあったろう。Gordan 問題の解決は、 「当時の大きな未解決問題が Hilbert により、予測困難な斬新な方法で解決された」と多くの人々を引き付ける様に書ける。しかし、「ネーター性が多項式環の構成に対して遺伝する」という有限基底定理は、数学を知らない人に対しては意味不明だし、それが20世紀の抽象代数学における証明や概念構成のスタイルに大きな影響を及ぼしたと言ったところで、20世紀抽象数学を知らない人には全く響かない。第一、大幅に「数式の学問」であった19世紀の代数学の話を数式無しで説明するのは「物」について語る事を禁止されながら物理について語る様なものだろう。

Reid の叙述のもう一つの特徴は、Gordan 以外の数学者の反応により、つまり、神学騒動以外の話で、この定理の革新性が強調されたことだろう。 実は、Reid の神学騒動の叙述は、案外に素っ気なく、Gordan が、"Das ist nicht Mathematik, das is Theologie." と言ったという事と、Klein は逆に、これにより Hilbert の才能を高く評価したということだけだったのである。それは、Klein の受け売りだったわけである。

Reid が最も詳しく説明した、数学者たちの実際の反応は、Gordan のそれではなく、Cayley のものだった。しかし、その叙述が、誤解に基づいていたのである。Reid は、Hilbert が Cayley に送った[Hilbert1888]の offprint に対して、最初、Cayley は、その様な証明ができるとは思えないと回答して来たことを書き、その後、次の様に続けた。

By January 30, however, having received two explanatory letters from Hilbert in the intervening time, Cayley was congratulating the young German: "My difficulty was an a priori one, I thought that the like process should be applicable to semi-invariants, which it seems it is not; and now I quite see. ... I think you have found the solution of a great problem."

しかしながら、1月30日までにケーリーは、ヒルベルトからの二つの手紙により、彼の疑問に対する説明を受け取った。そして、その後、ケーリーは、この若きドイツの数学者に 賞賛の辞を送りながら、次の様に書いた「私の困難はアプリオリなものでした。私はあの様なプロセスは semi-invariant に対して適用されるべきものだと思ったのです。しかし、それは間違いのようです。今は…と思っています。あなたは偉大な問題を解決したのだと思います」

Reid の叙述は、如何にも Cayley が有限基底定理に a priori な difficulty を覚えたと言っているかの様に書かれていた。しかし、Cayley が "process" と書いている所に注目して欲しい。 問題は、Reid が "now I quite see. ..." と、三つの点で省略してしまった部分にある。この部分には、数式が使われていて、おそらく、それが Reid が、著書に引用する際に省略してしまった理由なのだろうが、その部分の含めての "now I quite see. ..." の原文の画像と、その翻刻を示そう。

I now quite see that for invariants your step from \(i=a_1i_1+\cdots+a_mi_m\) to \(i=I_1i_1+\cdots+I_mi_m\) is quite right.

すでに、この2章の 2.1.2 で Hilbert の証明の概略を理解できていれば明かだろうが、Cayley が 「a priori な困難を覚えたが、もう分かった」と言っているのは、有限基底定理で得られた式に H-process を適用するステップなのである。つまり、Cayley は、有限基底定理と、その証明については、ここでは何も言っていないのである。

Reid は、この他に、Hilbert の師の一人であった Lindemann が、Hilbert の有限基底定理の証明に対して、unheimlich 気持ちが悪い、と言ったと書いている。しかし、調べてみたが、これのソースは分からなかった。

また、Reid は、1888年に、Hilbert が多くの数学者を訪問する大旅行を行い、 Göttingen の Klein を訪問した際には、非常に短くシンプルな Gordan 定理の別証明の論文を Mathematische Annalen に投稿したことを書いている。

その論文が、 [Hilbert1889] "Ueber die Endlichkeit des Invariantensystems für binäre Grundformen", "On the finiteness of the Invarianatsystem for binary ground forms" である。3章で、その内容を解説するが、この論文で、Hilbert は当時良く知られていた1次元射影空間版の代数学の基本定理を使う2変数不変式の表現を使い、Gordan の補題と呼ばれる線形ディオファントス連立方程式の解の有限性、そして、彼が考えたと思われる対称式などを使った簡単な補題の三つを使って、binary の場合の Gordan 問題、つまり、Gordan の定理の別証明を与えたのである。それは実に短く、また、シンプルで解りやすい証明だった。その為、今でも不変式論の教科書などで紹介されることがある。

この証明は、代数学の基本定理を使うために、本質的に2変数の場合にしか適用できない。しかしながら、この Gordan の補題が、というより、その補題が最初に証明された Gordan の論文[Gordan1873]の「証明の書き方」こそが、有限基底定理のヒントになったのではないかと私は考えている。これには、史料による直接的証拠はないが、そう考えたくなるような証明の書き方を Gordan はしているのである。これについては、3章の2.4で論じる。

この論文が、Reid が言及したものであることは、論文最後に記された、場所と日付、Göttingen, den 30. März 1888, Göttingen, 30th March, 1888, よりわかる。Reid の著書は、明らかに Hilbert Nachlass, Hilbert 遺稿集、の多くの史料の調査に基づいて書かれており、御本人は「自分は学者ではない」というスタンスであったが、明らかに、歴史学者が行う様なアカデミックで綿密な作業に基づいていたと言って良いだろう。しかし、もちろん膨大な Hilbert Nachlass ヒルベルト遺稿集 の全てを読むことは不可能であり読んでいない史料の存在も見て取れる。

その一つが、Hilbert と Klein の間の書簡である。これらは、Reid の著書の刊行の15年後の1985年に、スイスの数学者 Günther Frei が刊行した Hilbert と Klein の間の往復書簡[Frei1985]で、初めて容易にアクセス可能となった。

そして、これにより、様々なことの詳細が判るようになった。例えば、上で触れた論文[Hilbert1889]の証明の発見の大まかな経緯と投稿までの経緯が、Hilbert が Klein に向けて送った書簡から解る様になったのである。

この[Frei1985]は書簡を翻刻したものなので、いままで見てきた歴史についての叙述とは性格が違うが、これ以後の Gray, Rowe, 林, McLarty などの言及は、すべてこれに依存しているので、次にこれを簡単に説明しておく。

2.3.5. Frei による Hilbert Klein 往復書簡集

1985年に出版された[Frei1985]は、Göttingen 大学図書館の Hilbert archive と Klein archive の、それぞれへの書簡を翻刻し、また、それに多くのリマークや、Gordan から Klein への Hilbert の論文[Hilbert1890]についてのコメントの書簡なども、補足資料として付けた、非常に学術的に価値の高い史料集である。 非常に残念なことに、現在、この書籍は絶版となっているようだが、まだ、古書市場では手に入れることができる。私が最初に買ったものは、書き込みが相当あるので、東大講義のために、古書を一冊買い分解してスキャンしてPDF化し文字認識を実行した。以下に示す、このテキストからの文章は、それを使ってコピー＆ペーストした上で整形・修正したものである。

Frei はスイスの数学者かつ数学史家で、スイスのドイツ語圏の人であると思われるので、ドイツ語は母国語であろう。Klein と Hilbert の手書き文字は、時々、乱暴で何と読んで良いか分からなくなるものがあるものの、読むことにそれ程の困難はなく、私が原資料と、その翻刻を比較したのは、極少数の書簡だけではあるが、全般的に正確な翻刻が成されている様に見える。

この往復書簡集により、それまで判明していなかった歴史的事実が幾つか理解できる様になったと書いたが、その一つが、既に述べた[Hilbert1889]の Gordan 問題の極く短くシンプルな証明の発見の経緯であった。Reid の叙述では、Hilbert が Göttingen に Klein を訪問する前、Gordan に会ったことは書かれているが、どこで会ったかは書かれていない。おそらく Reid は、Hilbert が書いていた旅行の記録から、これを推測したのだろう。しかし、その旅行記には場所までは書かれていないので、それを書くことができなかったのだと思われる。

しかし、それが[Fei1985]により明らかになった。該当箇所は、同書のpp.38-39の Hilbert から Klein へ書簡27で、日付は、それぞれ、1888年3月16日である。この書簡で､Hilbert は次の様に書いている。

Ich bin hier in Leipzig in einem Hotel mit P. Gordan, welcher so gütig war, mir ein Rendez-vous hierselbst vorzuschlagen. Trotz mancher abweichenden Anschauung verstehen wir uns doch, glaube ich, recht gut. ([Fei1985], p.38)

I am here in Leipzig in a hotel with P. Gordan, who was kind enough to suggest a rendezvous here. Despite some differing views, I think we get on quite well.

要するに、Gordan の住む Erlangen ではなく、Leipzig で、Hilbert は Gordan に会ったのである。後で、この Leipzig での会合が重要なポイントとなる。また、Hilbert が意見の相違があると書いている事も重要である。Hilbert は、Klein への手紙では、このことを軽くにしか書いていないが、後に、Gordan の方は、相当に意見が違うと思って重要視していたらしい事が判明する。

[Frei1985]によって、詳細がよりハッキリと見える様になった事のもう一つに神学騒動がある。これに関しては、[Frei1985]には、次の様な情報が含まれていた。

1. Hilbert から Klein への[Hilbert1890]の Mathematische Annalen での掲載依頼。
2. それらに対する Klein の返事。特に、[Hilbert1888]の書き方を受けて、そのフル・ペーパー版の書き方への示唆。また、そのフル・ペーパー[Hilbert1890]の原稿を受領した際の最上級の賞賛。
3. Gordan の[Hilbert1890]の Math. Annalen への掲載が、今のままの証明では不適当という Klein への手紙を、Hurwitz に見せられた Hilbert が、Klein に送った激しい怒りと抗議の書簡。
4. 3の Hilbert の書簡の補足として、その Gordan から Klein への手紙の「掲載不適当」という意見の部分の翻刻。
5. Klein から　Hilbert への1890年4月14日の書簡(書簡番号56)での、Gordan が8日間、Klein の元に滞在し、その間、多くの議論をした。Gordan の意見は肯定的であり、心配する必要はない、詳細は、Hurwitz が直接説明するという連絡。

ここで、何故、Gordan が Klein を訪問し、8日も過ごしたのか、また、Könisgberg 大学教授で Hilbert の先輩ともいうべき Hurwitz が、Gordan の手紙を Hilbert に見せることが出来たのか、また、事の次第を Hilbert に直接説明できるのか、そういうことについては、[Frei1985]には、全く情報は無かった。これらは、今回の林の研究により、明らかとなったので、4章で、Klein, Gordan, Hurwitz の間の書簡の画像を見せながら解説することになる。

また、[Hilbert1888]と[Hilbert1889a]は、後者の方が先に投稿されたものの、前者が紀要の速報、後者が専門誌のフルペーパーという違いから、出版された時期が、ほぼ同時で、Hilbert は相次いで、その offprint を Cayley に送ったらしい。[Hilbert1888]に対する Cayley の肯定的な反応については、すでに述べたが、[Hilbert1889a]については、Cayley は関連した論文を書いて、Math. Annalen に投稿するなどしたが、それには誤りがあり、Hilbert, Klein, Gordan, そして、ノルウェイの数学者 Petersen との間で盛んに議論が闘わされたことが知られており、それらの書簡の翻刻も論文として出版されている。この時期の書簡を見ると[Hilbert1890]に関する情報と、これに関する情報が入り乱れるように書かれており、どうやら、両者には大きな関連は見られない様に見えるが、こちらの「論争」についての分析や、両者が本当に無関係だったかの検討は今後必要である。

話を戻そう。数式による数学的脚注も多く含まれた[Frei1985]は、明らかに専門家のために編纂されていた。これを読めた、非専門家は少数だったろう。しかし、この書簡集の出版の後、数学史家が、これに依拠して、一般向けの解説を書くようになる。その代表というべきが、次に解説する2000年の Jeremy Gray の解説である。

2.3.6. Gray の言及

Jeremy Gray は、英国の数学史家、数学者で、日本の放送大学にあたる Open University の教授を務め、現在は、名誉教授である。数学におけるモダニズムをテーマとした大部の著作 "Plato's Ghost" [Gray2008]など多くの著作で知られる。また、数学史の専門雑誌としては双璧と言える Historia Mathematica や Archive for History of Exact Sciences のエディタをつとめ、引退後の現在も後者のエディタをつとめている。また、国際数学者会議の招待講演者を務め、アメリカ数学会の fellow に選出されるなど、現在の数学史を代表する人のひとりである。

特に、数学におけるモダニズムの研究は、賛否両論があるものの、林のライフワークというべき、このサイトで公開を進めている「数学を中心とする社会の近代化の思想史研究」と関係が深く(林のものは、数学における歴史社会学的意味での Modernization の研究)、2018年に来日された際には、名古屋大での応用哲学会のシンポジウムで、Gray と林が提題者をつとめた(その時の林の提題講演の資料がこちら)。

西暦2000年は、Hilbert のパリ講演の100年後で、そのため、それを記念して様々な著書や記事が書かれたが、その内の代表的なものが、Gray による著書 "The Hilbert Challenge",[Gray2000]であった。この本は、基本的にはパリ講演と23の数学の問題の話がテーマなのだが、その他の多くのことについても書かれていて、様々な情報が詰め込まれていた。そして、その内のひとつが、Hilbert の Gordan 問題の解決と、それに伴う神学騒動の顛末の相当詳しい叙述だったのである。著作権の問題があるので、ここでは、少数の引用と要約しか提示できないが、Internet Archive の Open Library でオンライン借出しして読める。

林が知る限りでは、[Frei1985]で新たに判明した情報を元に書かれた神学騒動の一般向け解説は、この Gray の書籍が最初のようだし、それ以後、Gray による、この著書での、有限基底定理と神学騒動の叙述が、実質的な定説となったと思う。

Gray は、有限基底定理という名称を使うことは避けつつも、同書のpp.23-33の "Hilbert's breakthrough in invariant theory" で、1888年3月の Hilbert と Gordan の Leipzig での「共同研究」から、Gordan が Klein を訪問して、騒動に決着がつくまでを生き生きと描いてみせたのである。

それには、Gordan の数学が極めて計算中心だったこと、Hilbert, Gordan が Leipzig で会って数学の共同研究というべきものを行ったこと、そして、その後に、Hilbert が Gordan の数学とは全く異なるスタイルで、Gordan 問題を解いたこと、そして、それに対する Gordan の反応が書かれている。特筆すべきは、Hilbert の Gordan 問題の解決が、Kronecker の数学思想と対立するものであることが解説されながら、それまで一般向け解説で書かれていた間違えた Kronecker 像を修正すべく、Kronecker の Rationnalitätbereich の簡単な解説も入れて、当時、殆ど一般読者には知られていなかった Kronecker 研究の成果が解説されていたことである。

Kronecker が無理数の存在を認めなかったという、当時、広く信じられていた間違いも、有理数の近似列としては認めていたのだ、ということなどが解説されている。実際、Kronecker の「一般向け」の解説などでは、その近似の話なると、平気で普通の解析学の積分などを使っているし、ベルリン大での講義でもそうだったらしい。Gordan が「超越論的」などと言いながらも、ちゃんと中間値の定理を使っている様に、第一級の純粋数学である数論や代数から出てしまったら、郷に入っては郷に従えであったのだろう。 実際、Kronecker の解析学の講義録など読んでみると、極く標準的スタイルで話をしているのがわかる。すべての数学を算術の世界に還元すべきだという彼の主張は、実は、夢として語られていたのである。

この様に、Gray の解説は、全体としては優れたものだったのだが、しかし、何故か、二つ誤りが混じっていた。その内のひとつは、次の文の中のシングルクオート記号で囲まれた部分である。強調は、林による。

Hilbert and Gordan spent a good week together in Leipzig in the spring of 1888, after which HiJbert elatedly reported to Klein: 'With the stimulating help of Prof. Gordan an infinite series of thought vibrations has been generated within me, and in particular, so we believe, I have　a wonderfully short and pointed proof for the finiteness of binary Systems of forms.'　([Gray2000], p.23 より。elatedly は、喜んで、得意にして、の様な意味である)

この 'With the stimulating help of Prof. Gordan an infinite series of thought vibrations has been generated within me, and in particular, so we believe, I have　a wonderfully short and pointed proof for the finiteness of binary Systems of forms.' は、すでに[Frei1985]から引用した Hilbert が Leipzig から Klein に宛てて書いた書簡27に引き続く書簡28(同書p.39, その書簡のPDF化)から引用された、次の様な短いフレーズの英訳だった。

Unter der anregenden Hülfe des Herrn Professor Gordan ist inzwischen eine unendliche Reihe von Gedankenschwingungen in mir erzeugt und insbesondere habe ich, so glauben wir, herrlich kurze und pointirte Beweise für die Endlichkeit der binären Formensysteme.

その英訳を Google translate を使用して行ったものが次である。強調を入れた以外林は一切手を加えていない。

With the stimulating help of Professor Gordan, an infinite series of thought-vibrations has been generated in me and in particular I have, we believe, wonderfully short and pointed proofs for the finiteness of binary form systems.

強調部分を Gray の翻訳と比べて欲しい。実は、原文は複数の proofs なのであるが、Gray は単数の proof にしてしまっているのである。 念のために原史料の該当部部の画像を示す。

理由は分からないが、Gray は非常に単純なケアレスミスをしてしまったのである。そして、驚くべきことに、その後、この出来事について書いた私が知る限りのすべての著者が、同じミスをしてしまっているのである。その著者の一人は、私自身であり、私の場合は、Gray が著名であることから、Frei の翻刻を確認せず、その叙述を鵜呑みにしてしまったのが、その理由である。

しかし、後で詳しく説明する様に、明らかに Gray の叙述に依存していない著者も間違えている。その理由は、a proof と理解した方が広く知られていた事実と整合的だったからだろう。

すでに Reid が書いていたように、Gordan とあった後、Hilbert は、Göttingen に Klein を訪問して、その際に、Gordan 定理の短い別証明でる[Hilbert1889a]の原稿を手渡したことが知られたいた。そして、それ以外の別証明の方は忘れ去られていたからである。

実は、Hilbert は、もう一つの別証明を1889年に出版しているのである。しかし、それはリマークの様な議論の中でのことだった。読んだ人も少なからずいただろうが、それは実質的に忘れ去られていたのである。そして、この「忘れられた証明の存在」が私の新説のキーポイントとなる。これについては、この2章の3.2で、林を含む歴史家たちが、どの様な誤解、見落としをしていたかを説明し、それを如何に修正すべきかは3章で解説する。

もう一つの間違いは、次の強調部分である。強調は、林による。

Hilbert's discoveries bad been pubhshed as three short notes in a journal of Göttingen University. These were statements of results and, as wa quite customary, no proofs were given. The longer papers, complete with proofs, appeared in the more prestigious Mathematische Annalen.

Gray の神学騒動の扱いは、比較的簡単なもので、

Gordan's initial response has become famous, and must have spread rapidly around the seminar rooms and coffee tables where mathematicians liked to gather: 'This is not mathematics, it is theology.' ([Gray2000], p.29より)

これ以外に、Gordan が後に theology の価値を認めたことなどは書かれているが、議論は、主に Hilbert の証明の非構成性についての比較的数学よりの話が中心で、その中で、上に説明した Kronecker の数学の話などが詳しく述べられている。

そして、この Gray の著書の後、彼が著名であるだけに、その「Grayの説」とでもいうべき彼の歴史認識が、他の歴史家により継承されてしまったのである。そして、継承した歴史家のひとりが、私自身であった。

2.3.7. その後の言及: Rowe, 林…

Gray の言及の後、それとほぼ同じ話が、他の歴史家が書いたもの中で繰り返されるようになる。その典型が、すでに話題3で登場した David Rowe の[Rowe2005]であろう。 Rowe は、数学史のみを対象とする専門誌としては、おそらく唯一のものである雑誌 Historia Mathematica のエディタを務めるなど、代表的な数学史家の一人と呼んでよい人である。特に、話題3で述べた様に、"Mathematics in Göttingen" に特化すると、非常に広範囲の近代の数学史を対象とする Gray ではなく、Rowe を第一人者というべきかもしれない。

Springer社の数学雑誌 The Mathematical Intelligencer は、アカデミックな姿勢は崩さないものの、専門誌というよりマガジン的な性格が強いが、そのため数学史の話題も多く、Years ago という数学史についての連載があるが、Rowe は、そのコラムのエディタを15年ほど勤めていた。その間に、自ら、このコラムに "Hilbert's Early Career: Encounters with Allies and Rivals"[Rowe2005]と言う記事を書いている。題名を見ただけで、神学騒動がでてきそうだと分かるが、その通りで、上に引いた Gray の叙述が、そのままコピーされている。つまり、Rowe も Leipzig で Hilbert が得た別証明は一つだと考えた様だ。

ただ、Rowe の叙述には、Gray の叙述には無かった二つのことが追加されていた。その一つが、Gray が三つの速報での証明を "no proofs were given" としたところを、証明が書いてあったとこと、そして、その証明が間違えていたことが説明されていた。Hilbert は、第一速報[Hilbert1888]で、有限基底定理を Theorem I として、それの拡張である Theorem II と同時に数学的帰納法で証明しようとした。しかし、実は、Theorem II は間違えていたのである。後で Cayley による反例を使って詳しく説明する様に、この定理は成り立たない。

ただ、Rowe は、ここで奇妙な間違いをしている。実は[Frei1986]の書簡55の1890年3月3日づけの Hilbert から Klein への書簡には、彼が1888年に Leipzig で Gordan と会った際に、[Hilbert1890]の Theorem II の証明を議論したことが書かれている。Rowe は、この記述を誤解して、[Hilbert1888]の Theorem II の証明を議論したと書いたのである。

しかし、同じ書簡には、[Hilbert1890]の Theorem I は、Gordan と会った後の冬学期に得られたものなので、その証明について Gordan と議論したことは一度もないとも書かれているのである。 そして、[Hilbert1888]の Theorem II の特殊ケースが、[Hilbert1890]の Theorem I なので、Rowe の様に理解すると矛盾してしまうが、Rowe は気が付いておらず、[Rowe2005]を拡張して書かれた[Rowe2018]でも同じ間違いが繰り返されている。

また、この Leipzig での議論が、1888年3月の議論だったとしたら、Rowe は McLarty が[McLarty2012]で、そう主張したより早く(McLarty の論文は2007年の国際会議で読まれているので、数年早く)、1888年3月の時点で、Hilbert が有限基底定理の証明を得ていて、それを Gordan と議論したということになる。しかし、Rowe は、そういうことを少なくとも陽には主張していない。Rowe の、この叙述は何を主張したかったのかよく分からず、非常に奇妙な印象を与える。

Rowe は、すでに紹介した Klein の政治的側面など、数学そのものではなく、それを行った数学者の社会的側面に光を当てる歴史学では、大変に優れた仕事をした人だが、この人による数学の理論史についての論文は見たことがない。おそらく、残念ながら、Rowe は、数学的内容を十分理解できておらず、何か誤解をしているのだろう。

Rowe のもう一つのミスというのは、実は、Frei によるミスに由来するものと思われるもので、神学騒動の発端となった Gordan への Klein による Hilbert の論文のレビューの依頼が、Gordan が個人的に Klein に、Hilbert の証明への懸念を伝えていたからだというものである。

しかし、4章で Klein から Gordan への書簡の翻刻を使って明らかにするように、実は Gordan へのレビュー依頼の際には、すでに Hilbert の論文の出版がは決まっていたのである。Klein が Gordan にレビューを依頼したのは、Rowe の理解とは逆で Gordan による Hilbert 論文への賞賛のコメントを期待してのものだったようなのである。そして、この Rowe のミスは、3.1 で解説するように、Frei が Gordan から Klein への書簡に書いた ihm (彼に)という単語を何故か Ihnen (あたなに)と間違えて翻刻してしまったからなのである。実は、この Frei のミスを発見したことが、私の新説研究の発端であったのだが、そのことは3.1で詳しく説明することにして、ここでは「定説」についての話を続けよう。

Rowe が[Rowe2005]で二つの間違いをした事を書いたが、実は、それの拡張版の[Rowe2018]では、もうひとつ間違いが追加されてしまっている。[Rowe2018]では、[McLarty2012]の内容が反映されていて、神学騒動での Gordan の発言を、Noether が、Gordan 自身から聞いたとされているのである。これが誤りである可能性が非常に高いことは、すでに論証した通りだが、ドイツの大学で20数年数学史の教授を務めた人であり、ドイツ語には堪能であるはずだから、Noether による追悼文を実際に見ていれば、Klein への言及に気付き事情を理解した事だろう。おそらくは、Noether の追悼文を検証しなかったのだろう。多くの場合、歴史家は解釈を主にする人たちと史料の分析を主にする人たちに分かれると言われるが、Rowe は専ら前者の様である。

2.3.8. 定説のまとめと林の間違い

以上の様な定説をまとめると次の様になる。

1. 1888年3月、Hilbert が Leipzig で Gordan に合い、その助けもあって、Gordan 定理の短い別証明を発見する。そして、そのことを Klein に書簡で知らせている。
2. そのすぐ後、Hilbert は Göttingen に Klein を訪問し、その際に、Leipzig で発見した Gordan 問題の短い証明を論文としてまとめたものを Mathematische Annalen に投稿する。それが、[Hilbert1889a]である。つまり、Leipzig で発見した別証明とは、[Hilbert1889a]の証明であった。それは、 Gordan に由来する線形ディオファントス連立方程式についての補題が本質的に使われており、Gordan の助けも得て発見するに最もふさわしい証明だったと言える。
3. その後、Königsberg に帰った Hilbert は、有限基底定理と、それに基づく Gordan 問題の解を発見し、それを、最初、Göttingen 紀要に三つの速報として出版、その後、フルペーパーにまとめて Mathematische Annalen に投稿した。それが [Hilbert1890]である。
4. Mathematische Annalen のエディタである Klein は、その論文のレビューを、Gordan に依頼したが、Gordan は、有限基底定理の非構成的性格に、強く反発し、そのままの証明では掲載に相応しくないという意見を Klein に送った。
5. その手紙を Königsberg 大学教授の Hurwitz から見せられた Hilbert は、それに強く反発し、Klein に激しい抗議の手紙を送った。
6. それに対する返事で、Klein は、Gordan が8日間、Klein の元に滞在し、その間、多くの議論をした。Gordan の意見は肯定的であり、心配する必要はない、詳細は、Hurwitz が直接説明すると書いた。
7. Hilbert の論文は、無事出版され、数学界にその革新性で大きな衝撃を与えた。そのあまりの革新性に、Cayly はアプリオリな困難を覚え、また、Gordan の様な評価もあった。一方で、Klein は、この論文故に、Hilbert を Göttingen に呼ぶことを決意した。
8. そして、やがて、これが現代代数学の証明のパラダイムとなった。Hilbert の証明を一度は、「数学ではない、神学だ」と批判した Gordan も、Klein によると、後には「神学も役に立つことを納得した」という様になり、有限基底定理の証明の改善を行うようになった。

私は、その15年ほど前、Hilbert の数学ノートや Königsberg や Göttingen での不変式論講義の記録などの分析を元に、Hilbert の不変式論の時代の数学基礎論的思索についての数学史の論文を書いていた。しかし、その自分自身の論文の意義がわからなくなり、その結果興味が広がってしまい、結局、それは完成しなかった。今は、広がった興味に一応の結論がついて、この研究の意義も理解できるようになったので、日本語にして、こちらのWEBページにまとめつつある。

この完成しなかった英文論文には、まさに Gray と同じ間違い、つまり、速報には証明が書いてなかったこと、Leipzig で､Hilbert が[Hilbert1989a]の証明を Gordan の助けも得て考え付いた事、さらには、Gordan が、第一速報の offprint を受け取ったときの、Gordan の比較的肯定的な返信に、有限基底定理の form の無限列を一般のものではなく、制限した方が良いのではないかというコメントが書いてあることなどを書き、それは速報に証明がなかったために、そういう反応になったのだと書いた。15年も前の事で、さらにその間、随分違う分野の研究ばかりしていたので、もうすっかり、その頃のことを忘れてしまったのだが、どう考えても Gray の叙述を鵜呑みにしていたとしか思えない。

今回、所有している Gray の著書を、久しぶりに開いてみたが、該当箇所には、色々と書き込みをしていることと、2024年の夏まで、速報には証明がついて無かったと信じていたことが、私が鵜呑みにしていた事の何よりの証拠だろう。実は、夏に McLarty の論文への反論のための証拠集めを開始することにより定説の問題に気が付くまで、速報の内容は[Hilbert1890]と、ほぼ同じだと信じていて、読む必要はないと思っていた。これも歴史家としては、恥ずかしいことであった。実は、新説の鍵は、その速報の第三報に隠れていたのである。

例え、著名な人の説でも、鵜呑みしてはいけないという、そして、自分の記憶も信じてはいけない、という歴史家の態度として当たり前のことに反する悪い手本に自分自身がなっていたわけである。先ほど述べた英文論文の原稿を、WEB上に誰でもアクセスできるようにして置いておいたのだが、今回、間違えていることが判って、あわててサーバーから削除した。

岩波文庫「不完全性定理」でも、同様の間違いを書いているのではないかと、調べてみたが、幸い、その解説では、これについては何も書いていなかった。しかし、Reid の間違い、つまり、Cayley が有限基底定理に a priori な困難を感じたということは書かれていた。

3. McLarty の新説と定説の崩壊

Gray や Rowe の定説の後、ある奇妙な「論文」が書かれた。それが、アメリカの哲学者 Collin McLarty による[McLarty2012]である。論文に鍵括弧をつけたのは、保守的な歴史学者である私の目からは、果たして、これを論文と呼んで良いかどうか躊躇するからである。少なくとも、それは歴史学者が考える意味での論文ではない。

それが出版されたのは、2007年にギリシャの Delphi で行われた国際会議の講演の記録である "CIRCLES DISTURBED: THE INTERPLAY OF MATHEMATICS AND NARRATIVE" [Doxiadis&Mazur2012]という書籍であるが、Harvard の Barry Mazur の様な高名な数学者が参加し編集も担当しているが、歴史学者と言える人は、一人も関わっていないようなのである。

3.1. McLarty の異説

この論文で、McLarty は、様々な事を主張し、神学騒動の定説はあやまりだとした。彼の主張の内、「定説」と大きく矛盾することを箇条書きにすると、凡そ次の様になる。項目の順番は、[McLarty2012]での出現順とは関係ない。

1. Noether が Gordan の神学コメントに最初に言及し、その後、ずっと言及は無く、1922年に Hilbert の60歳を記念して書かれた biography にさえ、Gordan の神学発言はなかったが、翌1923年に、Hilbert 自身が[Hilbert1923]で、数学基礎論論争に関連づけて、それを語った。
2. そして、Klein が[Klein1926]で、Noether の話を繰り返し、また、それに色を加えた("Klein repeats Max Noether rather closely, but adds color:",[McLarty2012], p.121)。以後、Blumenthal, Weyl などの Göttingen の数学者たちが、神学発言について語った。ただし、"adds color" というのは、「後に、Gordan は、神学も役に立つと納得したよと言った」という話である。
3. Gordan は、Hilbert の有限基底定理の証明方法について反対はしていなかった。そればかりか、Leipzig で会った時、その証明方法を、Hilbert から聞いて知っていた。
4. Gordan が批判していたのは、証明方法そのものでなく、証明の書き方だった。
5. 神学云々というのは、Gordan の冗談だった。

最初の1,2の主張は、[Klein1926]の出版年だけを根拠に考えられた説だろう。実際の言及の順番は、すでに説明してきたように、Noether, Klein のものが、どちらも1910年代で最も古い。そして、Noether への情報源は、Klein だと考えられるのは、すでに論証した通りである。

ただ、その後、Noether の言及後、長らく公での言及がなく、1923年に Hilbert が口火を切っているというのは良い指摘である。 McLarty は、この Hilbert の言及が、当時の数学基礎論論争の影響だと考え、また、この基礎論論争のために、神学騒動が必要以上にスポットライトを浴びたと考えているようだが、この点については、私も同じ様に考えている。

岩波文庫[林、八杉2006]の、5.8で詳しく説明しているように、Hilbert は、1921年ころから、それまでむしろ友好的とさえいえた論敵 L.E.J.Brouwer と H.Weyl への態度をガラリと変えて感情的に敵対的になっている。そして、その中で、彼らの思想と Kronecker や Gordan のそれを同じ傾向のものとして、必要以上に貶めてしまった。そう考える歴史家は少なくないはずである。

この様に、実は McLarty の歴史観は、Gray や私の歴史観に近いのだろうと思う。しかし、その一方で、[McLarty2012]での歴史叙述の仕方には、もし、歴史のプロが行ったならば、他の歴史家から捏造とか歪曲と非難されそうなものが幾つもある。 また、初心者が行う様な稚拙な叙述もある。

例えば、1926年に Klein が Noether の言及を繰り返したかのように書いているのは、その一つである。 出版物を対象にして歴史学を行うときには、その出版年だけで、その出版物や著作時の時代を考えてはいけないというのは、歴史学の基本中の基本である。例えば、再版の際に大幅に書き変えられていることがあり、それを初版時の内容と誤解するというのは、歴史研究の手法を知らない素人が良く陥る過ちだ。私の場合は、すべての版を調べて、内容を比較することにしている。McLarty は、そういう歴史学の基本の手順を踏んでいない。

McLarty は、分析哲学とか、英米系哲学と呼ばれる哲学の専門家で歴史家ではないと思う。実は、私の京大文学部での同僚にも、そういう分野の人たちがいて、押しなべて、歴史無視の人が多かった。そうならば歴史について発言しなければ良いものの、結構発言したり書いたりして変な事を言う。注意しても、話が通じず、中には意識的にそうしているのだという同僚さえいた。それで、議論するのも馬鹿らしくなり、分析哲学者の歴史についての発言は無視するようになった。

という次第で、McLarty の論文は随分前から知っていたのだが、誤りを指摘するのも馬鹿らしいと放置していた。しかし、東大での講義の依頼を受けて、講義で歴史の作法を見せるには、恰好の例だと思い、[McLarty2012]の分析を進めた次第なのだが、それが定説の誤りの発見に結び付いたのである。 これは面白いことで、定説が間違えているために、間違えて、それに反論した McLarty の説は、誤りの誤りで、一部正しいのである。例えば、上のリストの内、3の「Gordan は、すでに Leipzig で、Hilbert の有限基底定理の証明を聞いていた」というのは正しい。また、4は、正しくはないのだが、Hilbert の論文の書き方が酷いものだったのは確かであり、Gordan が実際にそう批判したという史料的証拠もある。

歴史学とは、先人が書いた歴史の誤りを見つけ、それを修正することだ、と京大の歴史学者(別部局)が言っているのを聞いたことがある。実に良いことを言うなと思ったものだが、とはいうものの、歴史の素人に近いと思われる人の誤りを延々と指摘するのは、揚げ足取りの様で、あまりいい気分ではない。

そこで、これ以上、McLarty の歴史研究の作法に反する叙述をいちいちあげつらうのは止めて(つまりもっとある。捏造と呼べるほどのものが、他に少なくとも二つある)、私に定説の誤りを発見させた叙述の説明だけに留めようと思う。

3.2. McLarty の説を反駁しようとして起きた事

ということで、私に定説の誤りを教えた McLarty の「誤り」について説明しよう。それは、Gordan が自分の論文の不掲載を Klein に勧めた手紙のある文の英訳だった。McLarty も引用している[Frei1985]では、その文は次の様に翻刻されていた。強調は林による。

Ich habe es Ihnen wohl in Leipzig gesagt, dass mir seine Schlussweise nicht zusagt; er verlässt sich aber darauf, dass die Wichtigkeit und Richtigkeit seiner Sätze ausreicht.

I told you in Leipzig that I do not like his way of reasoning; but he relies on the importance and correctness of his statements being sufficient.

しかし、[McLarty2012], p.108 では、これが次の様に英訳されていたのである。これも強調は林による。

I told him in Leipzig that his reasoning did not tell me anything. He maintained that the importance and correctness of his theorems was enough.

McLarty の英訳の様であれば、Klein も Gordan が Leipzig で Hilbert に会ったことは知っているので、この時、問題となっていた有限基底定理、あるいは、それに類する定理の証明方法のことを言っていると解釈するのが自然となる。つまり、Gordan は、Leipzig で、Hilbert から「神学的証明法」を、既に聞いていたとする方が自然になる。ちなみに、"mir nicht zusagen" の英訳は、Google translate のものの方が自然のようだ(参考)。

一方、Frei の翻刻の様に、Ihnen あなた、つまり、Klein に言ったとするならば、別の機会に、Leipzig で、Gordan と Klein が合った時の話になり、Hilbert の証明方法一般についてのコメントと理解するのが自然だろう。Leipzig には Klein も在籍していたことがあるライプチッヒ大学があり、また、Mathematische Annalen を印刷配布していた B.G.Teubner社の本拠地であったので、二人が Leipzig で別の機会に会っていても不思議ではない。おそらく、私同様、多くの歴史家は、Ihnen という Frei の翻刻に何の違和感も持たなかったはずである。Rowe が、Gordan の懸念を Klein が個人的会話で知っていたと書いたのも同じ解釈から来ているのだろう。

McLarty が Göttingen の Klein archive の原資料を読んで、そう変更している可能性はあったが、引用元は [Frei1985]としてあり、ページ番号まで書かれていた。 私は、これは恐らく、McLarty が自説に都合が良い様に勝手に読み替えたのだろうと思い、講義で、証拠として Frei の翻刻を示しつつ「こういうことをしてはいけません。捏造になります」と言えるなと思った。

しかし、こういう時、念のため石橋をたたいて渡るのが本当の歴史家である。幸い、20年程前の Hilbert 研究の際、Göttingen 図書館に所蔵されている Klein と Gordan の間の書簡のマイクロ・フィルムを、全てプリントしてもらって持っていたので、それを取り出して読んでみた。私は、Kurrent は、殆ど読めないのだが、ihm と Ihnen の違い位はわかる。

ところが、なんと McLarty の英訳の方が正しかったのである。次の画像は、その後に、Göttingen に依頼して、作成してもらったカラー画像の該当部分である。2ページにわたって書かれているので画像が二つあり、赤線で囲まれたものが、問題の文で、青線で囲まれた部分が、 ihm である。

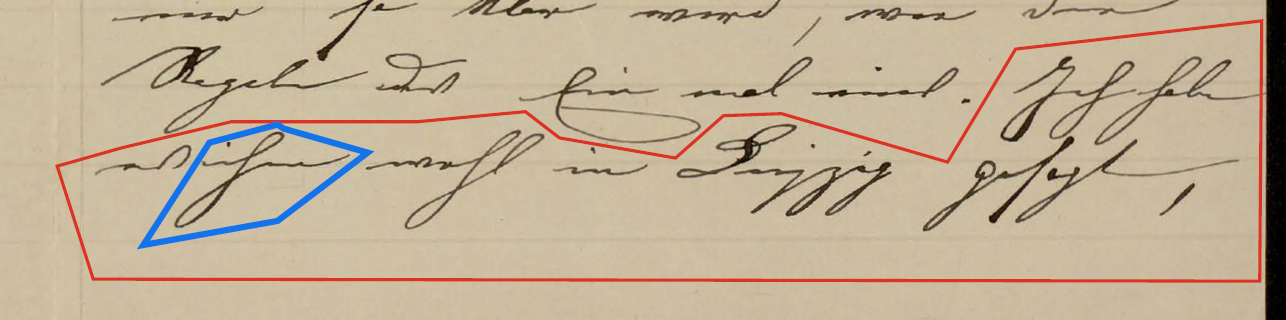
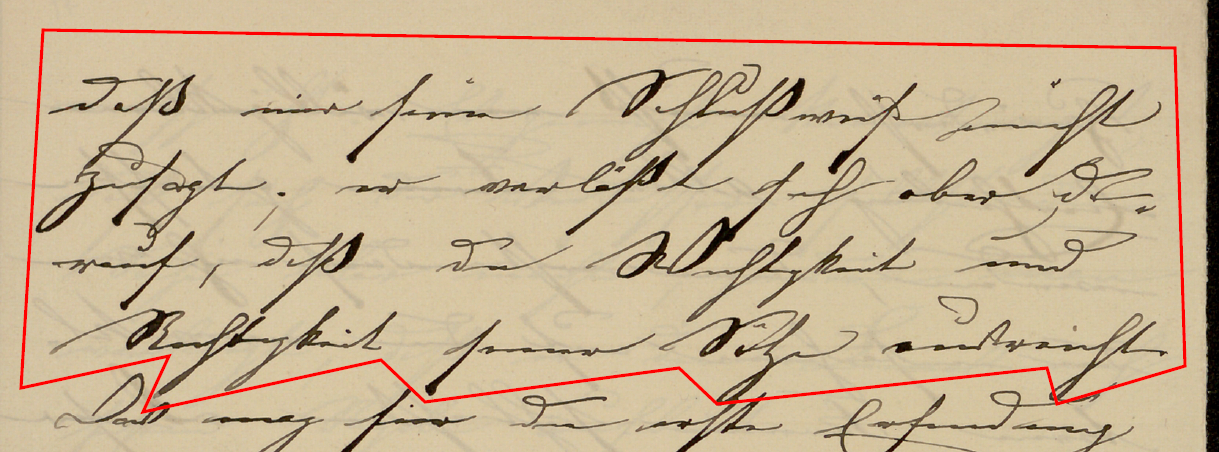
それまで全面的に信頼していた、Frei の翻刻に致命的なミスがあることが判り、それまで原資料の画像などは手に入れてなかった、Klein と Hilbert 間の書簡のすべての画像化を Göttingen に依頼して、一から再検討することを余儀なくされた。幸い、全部を見たわけでは無いが、Frei の翻刻は、上のもの以外は正確だった。

この発見で、何が真実なのか、暫く全く分からず混乱することになった。その時点では、先に翻訳の間違いを指摘した、Gray の

Hilbert and Gordan spent a good week together in Leipzig in the spring of 1888, after which Hilbert elatedly reported to Klein: 'With the stimulating help of Prof. Gordan an infinite series of thought vibrations has been generated within me, and in particular, so we believe, I have　a wonderfully short and pointed proof for the finiteness of binary Systems of forms.'　([Gray2000], p.23 より。elatedly は、喜んで、得意にして、の様な意味である)

私は、講義が出来なくなってしまうと思い、困ってしまって、あても無く、関係史料を、もう一度、読み返すしかなかった。そうしていたら、Gray の誤訳を発見してしまったのである。長く歴史研究を行ってきて、飛び上がるほど驚いた史料との出会いは何度かある。しかし、今回の様な経験をしたことはない。狐につままれる様な気分というのは、こういう事を言うのだろうと思った。Frei の翻刻の複数形 Beweise は何度となく見ているはずなのに、20年近く間違いに気が付かなかったからである。

もちろん、Hilbert が書き間違えたという可能性もないではないが、一つしか考え付いてない証明を二つ以上と書き間違えるとは考え難い。また、Beweise と複数形になってはいても単数の可能性も考えた。現代では、証明の単数は Beweis としか書かれないが、実は、この時代には、3格､Dativ の男性名詞は、語尾変化をして Beweise と、Beweis の複数と同じ形になっていたのである。Klein も Hilbert も、他の人たちも皆そう書いている。しかし、この場合の Bewiese は、haben の目的語で、"have" に対応するこの動詞の目的語は4格 Akkusativ なので、この語尾変化は適用されない。また、形容詞の語尾変化は、明らかに複数に対してのものだし、もし単数ならば einen と不定冠詞が付かねばならない。どう見ても、Hilbert は「複数証明を見つけた」と書いているのである。

ちなみに、McLarty も、実は同じ所を英訳していて、彼の英訳は次の様になっていた([McLarty2012],p.113)。

In particular we believe I have a masterful, short, and to-the-point proof of the finiteness of complete systems for homogeneous polynomials in two variables. (Hilbert and Klein 1985, 39)

本題にもどる。これで、もう一つ証明が必要になってしまったのである。しかし、そんなものがあるなど、どの様な書籍にも論文にも書かれているのを見たことがなかった。ところが、それが簡単に見つかってしまった。私が無視してしまっていた速報の第3速報[Hilbert1889c]にそれはあった。第3速報で、Hilbert は、[Hilbert1890]では Theorem II になっている整数係数版の有限基底理を Theorem VI として述べ、その詳しい証明を与えた後、定理という形ではなく、リマーク的に、それと自分の博士論文の結果を組み合わせると、Gordan 定理の別証明が得られると書いていたのである。しかし、それは、すでに、速報でも Theorem I と称されていた、体上の form の有限基底定理と H-process による Gordan 問題の解が得られている以上、もう不必要なものではあるがと Hilbert は書いている。

三つの速報は、1890年の論文に比較すると、不変式論に寄った記述になっていた。それに対して、実は、それを見た Klein が、フル・ペーパーは、不変式論の論文として書くのではなく、より一般的な代数に対する論文として書き、Gordan 問題の解決を、それの系として書くことを勧めているのである([Frei1985]、書簡41、1889年2月24日付)。つまり、Klein が[Klein1926]で述べたものと同じ Hilbert の仕事の捉え方である。

この様な書き方の変化や、可換環論がない時代であるために、実は1890年の Theoram II の証明の方が、Theorem I の証明より一般的ながら、少なくとも不変式論のために、この定理を使うことが不自然であったことなどの理由からであろう、「忘れられた証明」は、以後、語られなくなる。例えば、1897年の不変式論講義[Hilbert1993]では、全く触れられていない。そして、それにより、それは忘れ去られてしまったのである。というより、捨て去られたと言った方が良いのかもしれない。そして、それが大きな誤解を生んだようだ。

2章は、これで終り、次の3章、Leipzig で Hilbert が得た二つの Gordan 定理の別証明と、それを元に得られた Gordan 定理の証明がどの様なものであり、また、それらが公表された[Hilbert1888][Hilbert1889a][Hilbert1889b][Hilbert1889c][Hilbert1890]が、どの様に書かれていたのかを検証する。そして、上に書いた有限基底定理のルーツの問題を論じる。

脚注

[1] Hilbert を「現代数学の父」と呼ぶのは、日本では良く見かけるが、これは日本特有のことらしい。例えば、英語で例がないかと思い Google で検索してみると、father of modern mathematics として見つかるのは、主にデカルトである。これは modern という言葉の使い方が、日本と英語圏、あるいは欧州語圏で異なるからである。日本語には「現代」と「近代」という言葉があるが、英語では、どちらも modern としか書けない。もちろん、contemporary という形容詞はあるが、contemporary mathematics とすると「今日の数学」になって、たとえば、modern mathematics の典型と思われる Emmy Noether の代数学は含まれなくなる。デカルトが、father of modern mathematics というのは、「近代数学の父」という意味なのである。ただ、数学では、modern mathematics というと、日本語で現代数学というのと同じ意味で使われるのが普通だと思う。