
2017.07.11: クラスとすべきところが類になっていた所などを修正。
アリストテレス論理学の本体部分は、推論(正確には演繹)について論じるシロギズム、三段論法の理論である。
論理学と言えば、有名な三段論法
が引き合いに出される。
この様な演繹(推論)の正しさを体系づけたものが、三段論法の理論、シロギズムである。
アリストテレス論理学の説明の最後に、これを解説する。
上記の三段論法の、人間、死ぬもの、はどちらも名辞であり、2の「人間は死ぬものである」は、典型的なA型(AEIOのAということ)の命題、つまり、全称肯定命題である。
では、1の「ソクラテスは人間である」と「ソクラテスは死ぬものである」はどの様に考えるべきだろうか。
文章の形から、あきらかに、A be B の、A という主語の名辞は、「ソクラテス」である。
しかし、「ソクラテス」は、一人の人を表す項であり、「人間」とか「死ぬもの」などの集団を表す項とは違うようにみえる。
実は、ここにアリストテレス論理学の大きな特徴がある。
5月1日の資料で、高校数学の集合の定義の説明で使われる、外延、内包という言葉のルーツの説明をした。
再録すると、次の様になる(アリストレス論理学のルーツといえるポール・ロワイヤル論理学の英訳から):
Now, in these universal ideas there are two things, which it is very important accurately to distinguish COMPREHENSION and EXTENSION. I call the COMPREHENSION of an idea, those attributes which it involves in itself, and which cannot be taken away from it without destroying it; as the comprehension of the idea triangle includes extension, figure, three lines, three angles, and the equality of these three angles to two right angles, &c.
I call the EXTENSION of an idea those subjects to which that idea applies, which are also called the inferiors of a general term, which, in relation to them, is called superior, as the idea of triangle in general extends to all the different sorts of triangles.
ここではtriangle 三角形という term の内包と外延が説明されている。外延 Extension の方は簡単で、すべての三角形の全体、つまり、三角形の集合ということで、現代的な「外延的定義」、つまり、三角形全部を並べあげる定義と意図が一致する。
内包 Comprehension というのは名辞の「本質」のようなもので、これを説明するのは難しい。
実際、これの説明は、色々なアリストレス論理学の本を見ると、それぞれ微妙に異なる。
「本質」のような哲学的な概念を、スッキリ説明することは困難なのである。
一方で、外延は、集合という概念を理解していれば簡単である。
「三角形」 "triangle" という名辞の概念は、それが指し示すもの全体、つまり、三角形と呼ばれるものの集合なのである。
これが集合だから、上に説明した categorical proposition の4つの型 AEIO を、集合の図(ベン図)を使って説明できたのである。
つまり、このAEIOの説明では、どのような名辞も、その属性 attribute の一つとして外延とよばれる集合を持っていることになる。
上のComprehension 内包の説明で三角形の内包の説明で、"as the comprehension of the idea triangle includes extension, figure, ..." と、先頭に書かれているように、
これは名辞の使われ方を完全に説明するもので、数々ある内包の属性の内でも最も重要なものとも考えられる。
実際、a be Triangle という categorical propositon の真偽を知るには、Triangle の外延だけあればよい。その意味で外延は、名辞の本質の大半を担うものといえる。
注.この説明と、クンマーの理想数とデーデキントのイデアルと切断の説明は似ている。その意味を考えてみて欲しい。
実は、この外延のみを独立させて、厄介な「内包」を、高校数学で行うように外延(集合)の定義を行う時に使うものと限定したものが、現代の集合概念だと考えることができる。
いずれにせよ、アリストテレス論理学では、「ソクラテス」という名辞の外延は、集合のような、ものの集まりということになる。
それは「固有名詞」なのだがら、当然、集合の要素の数は一つでないといけない。
名辞「ソクラテス」の外延は、ソクラテスという人、一人を要素とする「集合」と考えるのである。
つまり、次が、名辞ソクラテスの外延なのである。

そして、この様に考えると、上の三段論法
の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ
の形、しかも、すべてがA型の全称肯定命題であることがわかる。
つまり、
の本当の意味は、
ということになる。
不自然なようにも感じるが、
という命題も、恐竜が絶滅寸前で、恐竜が最後の一ぴきしかいない状況では、「ソクラテスは人間である」と同じ様な状況となることを考えれば、必ずしも可笑しな理解ではない。
先ほどの三段論法の前提、つまり、1-3の内の、1と2
の状況を、今までのようなベン図で重ねて図示してみると
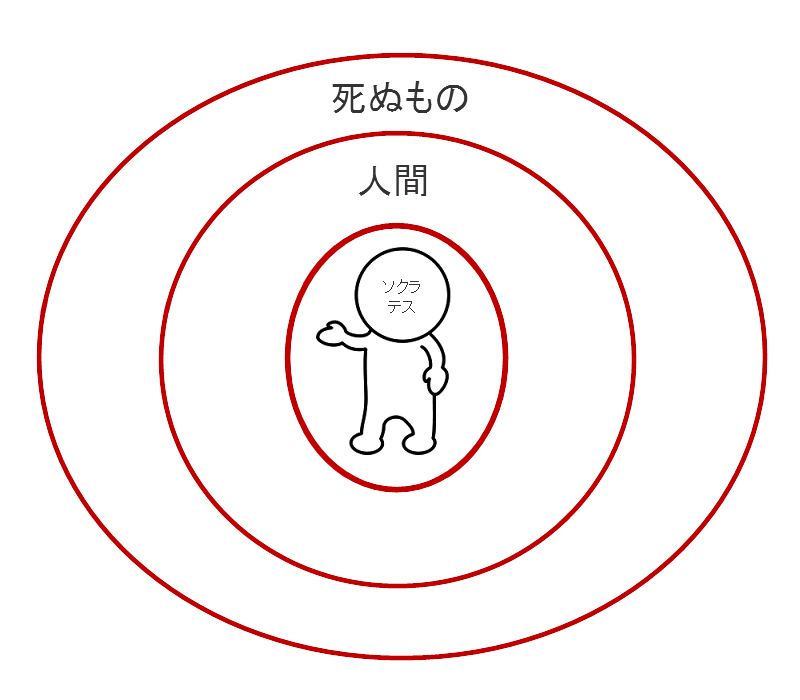
となる。あきらかに、
が分かる。つまり、有名な「ソクラテスは死ぬ」という三段論法は、数学でいう
つまり、
のことである。
これは
がどちらも全称肯定命題として理解されたとき、 A be B B be C の、中間の B をとって作った A be C という全称肯命題は、二つの前提が正しいときには正しいことを意味している。
同様のことを、1、2 と A be C のそれぞれを、全称肯定、全称否定、特称肯定、特称否定のすべてのパターンで考えて、その推論が正しいかどうかを、ひとつひとつ検討したもの。
それがアリストテレス論理学の主要部分であるシロギズムの理論(三段論法の理論)であった。
また、Keynes の教科書の59頁にもあるように、実は、「ソクラテスは人である」という命題は、「ソクラテスという人がいる」という特称肯定命題と考えることもできる。
この様な特称名辞を主語にする categorical proposition の奇妙さは論理学者の間で議論があったらしい。
多くの論理学書が書かれたが、Keynes の教科書が、その典型である様に、この「特称名辞」の問題は、常に喉に刺さった棘であったのである。
そして、次に説明する「数理論理学」で、初めて、この問題が解決される。
アリストテレス論理学の問題点として、上に挙げた特称名辞の問題と並んで、二つの問題があった。
それは、
という問題だった。
1番目の問題は、例えば、「AはBとCを両親とする子供である」のようなものを直接的に表すことができないという問題である。
このような時、アリストテレス論理学では、たとえば、「Aは両親Dの子供である」、「Bは両親Dである」、「Cは両親Dである」など、不自然な表現しかできないのである。
また、2番目の問題は、リンク先シロギズムの理論で見た様に、正しい推論のパターンは、一つ一つ吟味すればわかるものの、
それを説明する統一的な方法がないという問題であった。
そのため、シロギズムの理論のテーブルにある Barbara, Barbari の様に、これを覚えるための符丁さえ発明されていたのである。
そして、19世紀になると、これらの問題だけでなく、哲学、言語学、数学などの様々な動機の元に、論理学の見直しが始まり、
20世紀の初頭まで、その論理学の改革の運動が続いた。
その多くは、現在では忘れ去られているが、たとえば、ジョン・スチュアート・ミルやジョン・デューイなどの著名な学者たちが、
新論理学を提案したのである。
実は、禅などに結び付けて考えられがちな西田幾多郎の哲学も、そして、京都学派の哲学者たちの多く哲学理論も、
新論理学の創出を目指したものだと考えることもできるのである。
そして、第二次世界大戦後、特に1970年位から、そういう様々な「新論理学」の中で、ある一つの流れが、
外を圧倒して強くなり、現在、例えば日本では、ほぼ完全に「論理学」の地位を占めるようになったものがある。
それがイギリスの数学者ジョージ・ブールに発する、数理論理学である。
このブールの数理論理学は、哲学の一分野であるアリストテレス論理学への代数学の応用だったが、
アメリカの万能学者チャールズ・サンダース・パースなどにより、大きな改良がくわえられ、上に書いた三つの問題がすべて解決された。
これがイタリアの数学者ペアノにより、数学の記述に応用されるようになる。
そして、その影響を受けた、イギリスの哲学者兼数学者バートランド・ラッセルによりペアノの論理学が拡張され、
20世紀の冒頭に、数学の近代的基礎の原型が完成する。
しかし、次回説明する、ラッセルのパラドックスが発見され、数理論理学は一度危機に陥る。
それを、ラッセルと、アルフレッド・ホワイトヘッドが、Principia Mathematica という危機回避策を作りだし、
これが、後期の特殊講義の主役となる、ヒルベルトとその弟子たちのヒルベルト学派に継承され、
数学の近代的基礎の創出に応用されたのである。
このブール→パース→ペアノ→ラッセル→ヒルベルト学派という系譜が、第4、あるいは、第3のルートである、論理学ルートなのである。
前期では、この内、ラッセルが、彼のパラドックスを発見するまでを解説する。
まずは、この系譜の源、ブールの話から始める。
イギリスの数学者ジョージ・ブールは、代数学の一分野、不変式論の創始、演算子法という微分方程式の解法の発明(解析学)などでも知られる数学者のブールは、
アリストテレス論理学の「categorical proposition は二つの名辞の関係しか扱えない」、「シロギズムの理論に一貫した統一性がない」という欠点を解消すべく、
名辞を代数式の変数 x, y, ... で表し、これの演算、たとえば、積 xy などを考え、数式のようなものをで名辞のようなものを表し(ブールの式には、名辞として解釈でないものが入っていたので、式がすべて名辞なのではない)、それを等号で結び等式を作り、代数と同じく、幾つのかの規則を決めて、その等式を変形することにより、シロギズムの理論を置き換えた。
たとえば、彼の1854年の著書 The Laws of Thought では、x を「白いもの」white things, yを「羊」という名辞だとすると、xy は「白い羊」を表す、と説明して、
xy=yx
が成り立つ、と説明している。
ブールは、categorical proposition を表すために、v という記号を導入し、たとえば、All Y's are X's を y=vx と表現したが、これは現代的な立場からは、全く受け入れることができない方法であり、現在では使われていない。
しかし、ブールが、名辞を使い、categorical proposition を彼の論理学の式で表そうとしたように、これはアリストテレス論理学への数学的方法の応用である。
つまり、哲学の一分野に数学を応用したものであった。
また、ブールがアリストテレス論理学を否定したという説明がされることがあるようだが、これは間違いで、ブールはアリストテレス論理学を改良しようとしたといえる。
さらに現在、ブール代数と呼ばれるものがあるが(1、2)、これはブールの論理学とは大きく異なるものである。
最初の数理論理学といえるブールの論理学では、「ソクラテス」の様な特称名辞が、「人間」などの名辞と同じ名辞であるという所は、アリストテレス論理学と同じであった。
しかし、アメリカの万能学者パースは、ブールの論理学の、この部分を見直し、1870年代から1880年代にかけて、関係の論理学 logic of relatives というものを創出した。
これが現在の述語論理学というものの先駆けである。
注.実は、ほぼ同じようなものが、ドイツの数学者ゴットロープ・フレーゲにより、ほぼ同時期に出版されているのだが、数学者のフレーゲの仕事は、ラッセルの仕事を通して、それが知られるようになるまで、ほとんど知られることがなく、特に数学者に与えた影響は非常に小さい。そのため、これは、この講義では取り扱わない。一方で、パースの論理学は、数学者ペアノの論理学の元となり、やがて数学の近代的基礎で使われることとなった。パースは、様々な分野で仕事をしているが、プラグマティズムの創始者であることもあって一般的には哲学者として捉えられることが多い。そのパースの論理学が、数学の基礎となっていったのに比べ、数学者フレーゲが数学に影響をあたえることがほぼなかった一方で、分析哲学と呼ばれている英米系の哲学には、今でも大きな影響を与えていることは、面白いことである。
パースの論理学には、三つのポイントがあった。それは
である。
この最初のものが、特称名辞の特殊な取り扱いを論理学から放逐することとなった。
アリストテレス論理学では、
A loves B
のような二つのもの関係を記述するとき、
A is a lover of B
の様に書く。
また、
A benefits B
は同様に categorical proposition
A is a benefactor of B
に翻訳する。
しかし、パースは、このような二つのもの関係を記述するとき、
i loves j
i benefits j
を、数学の記号を使って、それぞれ
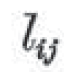
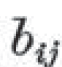
と書く方法を導入した。
パースは、これらを関係 relation と考え、自分の論理学を logic of relatives と呼んだが、
現代では、これらを
L(i,j)
B(i,j)
と書き、述語と呼んでいる。
アリストテレス論理学では、
A be B
が基本で、これは集合論の記号を使えば、
A⊆B
だったのだが、
パースでは、
L(i,j)
が基本で、これを集合論の記号を使えば
(i,j) ∈L
のように考えるのである。
ただし、 (i,j) は、i と j の対(数学では順序対という)である。
この様な述語の記号(述語記号)を導入したパースは、
さらに、quanifier 量化子と呼ばれる記号Π、∑を導入して、
「全ての者は、誰かを愛しており、また、その者に施しをなす」
あるいは
「全ての者は、誰かを愛しており、また、その者に恩をなす」
を、
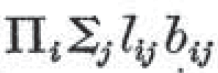
と書いた。
パースが行った述語の導入は、数学の関数
f(i,j)
や数列
aijのような記法にならったものである。
量化子は、さらに数学の記法を論理学に応用したものである。
これを説明しよう。
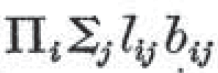
の
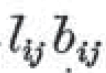
の部分は、 lij と bij の掛け算を意味している。
ブールでは、掛け算は、二つの名辞の共通部分を表していたが、
パースには、もう名辞の概念がなく、述語になっている。
パースでは、
L(i,j)
は
(i,j) ∈L
のように proposition、つまり、命題と理解されるので、
それは categorical proposition と同様に、真になるか偽になる。
そこで、1を真、0を偽と考えると、
1×1=1
1×0=0
0×1=0
0×0=0
となるが、これは
真かつ真 は 真
真かつ偽 は 偽
偽かつ真 は 偽
偽かつ偽 は 偽
という「かつ」の真偽の規則と一致する。
+の方は
1+1=2
1+0=1
0+1=1
0+0=0
となるが、2は1以上なので、1とみなすと、
1+1=1
1+0=1
0+1=1
0+0=0
となり、これは
真または真 は 真
真または偽 は 真
偽または真 は 真
偽または偽 は 偽
という、数学でつかわれる「または」と一致する。
さらに、マイナスを否定とみなして、
-0=1
-1=0
と定義すると、
真の否定 は 偽
偽の否定 は 真
で、これも代数が真偽と否定の規則を、そのまま表現することになる。
この考えをさらに発展させたものが量化子である。
たとえば、
All persons love Tom.
を考える。
数学の変数(あるいは添え字) i が人間、つまり、persons を表すとする。すると、この文章は、
All i love Tom.
になる。さらにパースの述語記号を使い、Tom を j と書くと、これは、
All i lij
と書ける。
ところが、もし、人(persons)にすべて通し番号がついているとすると、 i や j は、0, 1, 2, 3…という数字だと思ってもよい。
もし、Tom の番号が5番だとすると、これは、
All i li5
と書ける。
ところが、これは
l05 かつ l15 かつ l25 かつ l35 かつ l45 かつ l55 かつ l65 …
つまり、
l05 × l15 × l25 × l35 × l45 × l55 × l65 …
つまり、
l05 l15 l25 l35 l45 l55 l65 …
のことである。
数学では、こういう数列の積を
Πi li5
と書く。これがパースのΠの意味であり、それは、「すべての i に対して、li5 である」を意味している。
同じように、以上の説明の「かつ」、つまり、ブール代数の掛け算を、ブール代数の足し算、つまり、「または」に置き換えると、
l05 または l15 または l25 または l35 または l45 または l55 または l65 …
つまり、ブール代数の記法では、
l05 + l15 + l25 + l35 + l45 + l55 + l65 …
となるが、これは数学の記号を使うと、
∑i li5
になる。これがパースの∑の意味で、それは、「ある i に対して、li5 である」を意味している。 つまり、「誰かが Tom を愛している」「ある人が存在して、その人は Tom を愛している」となる。
以上の説明から、
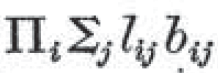
を直接的に日本語に訳してみると、
すべての人 i に対して、ある人 j が存在して、i は j を愛していて、かつ、i は j に施しをする
と読める。つまり、
全ての者は、誰かを愛しており、また、その者に恩をなす
と読める。
ただし、この「愛」はキリスト教における愛で、パースは、
これらの例文をトマス・アキナスの神学大全からとっている。
そのことからもわかるように、パースの目的は、ブールの場合と同様に、
アリストテレス論理学の改善であり、数学を応用しているが、
数学の基礎付けに、これを使おうとはしていない。
パースにとり彼の論理学は、彼の記号学の一部分だったといわれている。
最初、数理論理学は、言わば、数学の哲学への応用だったのである。
しかし、これが次のペアノで大きく変わる。
イタリアの数学者ペアノは、正方形を埋め尽くす連続曲線として知られるペアノ曲線(幾何学)、微分方程式のペアノの存在定理(解析学)、ベクトル空間の公理系(幾何学)、そして、Latino sine flexione という人工言語などの発明・発見や、当時の数学に大きな貢献をしたペアノ学派と呼ばれる多くの追従者・弟子たちを生んだことで知られる、実に多才かつ多彩な人だったが、もっとも有名な業績は、おそらく、その数理論理学と、それによる数学の形式化のプロジェクト Formulario mathematico (以下、Formulario)であろう。そして、これがイギリスの哲学者・論理学者・数学者のバートランド・ラッセルに影響を与えて、現代的な数理論理学が生まれる切っ掛けを作った。
実は、ペアノが数理論理学で行ったことの多くは、ドイツ、イエナ大学の数学者フレーゲが、それよりかなり早く、しかも、厳密性、徹底性に関して言えば、ペアノより優れた方法で、行っていた。しかし、フレーゲの研究は、ラッセルの仕事が広く知られたとき、それを通して広く知られるようになったものの、概念記法 Begriffschrift と名付けられた彼の論理体系は、記述、印刷、学習が難しい、奇妙な記法を用いるものだったために、他に影響を与えることが、殆どなかった。
たとえば、ラッセルは、Begriffschrift (著作の題名である)をペアノ仕事を知る前から、彼の哲学の先生だった James Ward からもらっていたが、指導教員もラッセルも、その価値に懐疑的であったためか読んでおらず、ペアノの仕事を理解した後で、漸く読み、その意味を理解したことが知られている。おそらくは、フレーゲが、数学者ながら、数理論理学の開拓と、その数学の基礎づけへの応用、および、哲学的な業績しかなく、数学上の業績がなく無名であったったことも影響しているのだろう。その様なフレーゲに比べれば、上に述べた数々の業績で、ペアノは当時の数学のスタープレイヤーの一人と言えたのである。
そのペアノのフレーゲへの対応は、その時代としては例外的で、彼はフレーゲの難解な記法を(ある程度は?)読み解き、自身の仕事との関連を理解して、フレーゲと書簡を交わした。また、フレーゲの著作の書評を発表したりしている。(このペアノとフレーゲの関係についての説明は、H.C.Kennedy: Peano: Life and Works of Giuseppe PeanoのChap.10を元にしている。)しかし、ペアノに大きな影響を与えたのは、むしろ、別のドイツの数学者、Ernst Schröder の論理学、一般に、代数的論理学と呼ばれているものの方であったようである。そして、その Schröder に大きな影響を与えたのは、フレーゲでなくパースだったのである。
ペアノの数理論理学の最大の特長は、それが数学を基礎づけるために開発された点にある。これはフレーゲの論理学も同様だったのだが、実際に、ペアノの数理論理学の時代までに、フレーゲが成し遂げていたのが、自然数の理論迄であったので、数学者のセンスからすれば、フレーゲの論理学は、論理学のための論理学に見えただろう。実際、ペアノは、そのように誤解していた可能性があることが、フレーゲの著作に対してのペアノの書評から伺える。
フレーゲの論理学では、論理的な正確性、厳密性が、当時の時代を遥かに超えたレベルで達成された一方で、肝心の数学という学問体系への視線が大幅に失われていたと言わざるを得ない。フレーゲは公式には数学者でありながら、哲学者化していたといえる。これに反して、ペアノは、飽くまで数学者であった。彼の数理論理学は、ペアノ自身にとっては、数学を学ぶ学生や数学者が、自然言語の曖昧性により惑わされることなく、数学の知識を正確に理解するための道具だったのである。
例えば、ペアノは、その数学的業績の一つである、微分方程式のペアノの存在定理を、ゲッチンゲン大学の数学雑誌である Mathematische Annalen に彼の数理論理学を使って投稿した。現代の状況では、これもまた、驚くべきことに、それは実際に掲載されたのである。このリンク先が、それである。
しかし、ペアノの意気込みとは、裏腹に、この様な人工言語による、数学論文の記述は、数学者には受け入れられなかった。ペアノは彼の Formulario mathematico を大学での教科書として使うこと、そうすれば、教授は数理論理学の記法さえ学生に教えれば、数学的内容は学生が自分で学べると主張したが、これは「人間は世界を論理的な思考により理解している」という意見で、非現実的な主張であった。実際、人間が数学を理解する際の非論論理的思考、特に直観や想像力が果たす役割は、非常に大きく、それなしでは現実の数学は成り立たないことは、リーマンの事例を見れば明らかと言える。そのため、ペアノの、この主張は、数学者や学生たちには、受け入れられなかったのである。
しかし、同時に、一旦生み出された数学が、理論的には、 Formulario のような人工的な言語で、ほぼ記述可能であり、その故に、現実的に数学の公式的基礎となり得るということは、この後の歴史が証明したことであり、それが数理論理学嫌いが多いブルバキの数学者たちが、公式にはブルバキ構造主義の基礎に数理論理学据えたことの理由であるといえる。
さらに複雑なことに、この可能性は、飽くまで理論的な可能性であり、それを実行に移すには、莫大な作業が必要であり、その量の問題故に、例え、ITの補助を得たとしても、数理論理学で現実の数学の記述を行うことには大きな困難がある。また、少なくとも、それは、最近の人間の棋士より強い AlphaGo のようなゲーム人工知能の動きが、人間の数学の理解とは大きく異なると言われるように、あるいは、それ以上に、人間の数学とは異なるものであり、人間の活動としての数学においては、特に数学の教育においては、受け入れられないものである。ペアノの希望は楽観的過ぎたといえる。
人工言語である、数理論理学による数学記述は、理論的には可能で、ITを使えば、現実にも、ある程度は実行可能なのだが、実際の生身の人間には異様なのである。Formulario の様なものは、人間の認識の方法とあまりにかけ離れ過ぎている故に、人間は、それに違和感を持つ。それがブルバキ数学者たちが、公式には数理論理学を、その思想の基礎に置きながら、数理論理学を嫌う様な姿勢を取り続けた理由のひとつでもあるだろう。
これらの事実の詳しい説明が、後期の講義の大きなテーマとなるが、今は、ここまでにして、先を急ぐ。
上に述べた様に、論理学が「数学を記述するための言語」として、捉えられ、しかも、実際に記述が試みられたということは、ペアノの論理学の非常に大きな特徴である。
ペアノの数学の記述の方法は、公理的であり、後で述べるラッセルやデーデキントの「論理に数学を還元する」という論理主義ではなかった。
つまり、講義の最初の方でやった、数学の対象を、それが満たすべき公理を設定した上で、それに基づいて、数学を行う、という方法だった。
現在も使われるベクトル空間の公理系は、その一つであるが、これは体や環と同じく、それを満たすシステムが沢山ある公理系である。
これに対して、実数のように、公理系を満たすものが唯一になる公理系としてペアノが考えたものに、今も「ペアノの公理」と呼ばれて広く知られている自然数の公理がある。
後で述べる様に、ペアノの、この様な方向と違い、デーデキントとラッセルは、デーデキントが切断で実数を「定義」したように、論理学を使って自然数を定義したのである。
この他の大きな技術的特徴に、現代の集合の記号で書けば
a ∈ b
と
a ⊂ b
が異なることを指摘して、異なる記号で記述するようになったことがある。
先に指摘したように、伝統的論理学では、この二つが、共に
ソクラテス be 人間
人間 be 死すもの
のように、同じタイプの命題とされていたのであるが、ペアノは、この考え方を退けたのである。
実は、今も使われる、この∈と⊂という記号がペアノに由来している。
⊂はラッセルが向きを反対方向にしてしまったが、元は、C の活字を上下逆にしたものから来ており、Ͻ と書いた。
この二つは、前者は、英語の is にあたるギリシャ語のεστιの頭文字からきており(正確にはアクセントがつくが略)、後者は、ラテン語の continet (英 contain) の頭文字を意味していた。
そして、パースがΠ、Σと書いた量化子 quantifier を、ペアノは、(x)、∃と書いた。現在は、これらは∀、∃と書かれる。
この他にもペアノが使い始めた記号が、数理論理学や集合論で使われている例は多い。
このようにペアノの後代への影響は非常に大きかった。そして、それは1900年にペアノに合い、その論理学を知り衝撃を受けて、自身の数理論理学を建設したラッセルを通してのものだった。
英国の哲学者バートランド・ラッセルは、最初、新ヘーゲル主義の立場から数学の哲学を考察していた。
しかし、1900年に開催されたパリ万博に合わせて開催された第一回国際哲学会議に参加し、ペアノと彼の学派の人々に遭遇し、彼の哲学の方向がガラリと変わった。。
ラッセルは、その会場で、ペアノが、他の哲学者・数学者を次々と論破することに強い印象を受け、それがペアノの数理論理学のためであろうと推測し、ペアノやペアノ学派の著作を受け取り、英国に引き返し、猛烈な勢いで、彼自身の論理学と、それによる数学の基礎づけの研究を開始したのである。
注. この辺りの歴史を、一時資料を駆使しながら、詳細に研究したものに、D. Gariciadiego のこの本がある。何故か、あまり知られていないが、非常に詳しい研究であり、例えば自伝でラッセルが、パリでペアノたちから、彼らのすべての著作を受け取ったかのように書いているところがあるのだが、実際には後から郵送されたものがあることまで調べ上げている。
ラッセルのペアノとの出会いを、ラッセルの自伝にみてみよう:
ペアノ論理学を継承する自身の論理学で、ラッセルが成し遂げたことは、1903年に出版された The Principles of Mathematics で、次のように説明されている.
ラッセルが主張したのは、数学のすべての概念、自然数とか、実数とか、複素数とか、幾何学空間、微分積分、
あるいは、それらより遥かに高度な専門的概念がすべて記号論理学の言葉だけで定義できて、
しかも、それらについての定理が、すべて、わずか20個の前提(公理)から論理推論だけで証明できるということである。
つまり、数学を完全に書ききることを可能にする言語と真理の素のようなものを、 わずかなページ数で書ききることができたということである。
ラッセルの論理学を、現代的に書けば、
であった。ただし、類(Class)というのは、ラッセルの用語で、アリストテレス論理学の名辞、特に、その外延だと思えば良い。
先に見た、ケインズの論理学の教科書でも、名辞の説明に class という英語が使われており、
このころ、物の集まりを表す用語として、class が使われていたことを示唆している。
ただし、外延なので、簡単に言えば、集合である。
実際には、ラッセルは、1903年の段階では、
クラスを数学者が考えた集合と、全く同じものだと割り切るところまでは行っておらず、
論理学の概念である、延々と内包について議論しているが、やがて、これは集合と実質同じ様に扱われるようになる。
ここでは、話を簡単にするために、割り切って、クラスとは、集合のラッセルによる別名だと理解すればよい。
これらのラッセル論理学の構成要素の内で重要だったのが、内包の公理と呼ばれるもので、
F がClass, Belong, Equal という述語のみを使う論理式ならば、あるクラス a があって、それは、Fがあらわす条件を満たすもの全部からできている.
というものである。
ここで、論理式という言葉を使ったが、これは、パースの論理学の所でやった
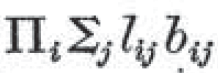
のような表現のことである。
ただし、この例では、l, b という「述語」が使われているが、ラッセルの論理学では、それをClass, Belong, Equalの三つに限るのである。
クラスは、集合と同じと思うことにしたので、Belong(a,b) は、数学とおなじく a∈b とかくことにしよう。
実は、内包の公理は、高校の数学で実質学習している。
内包の公理が存在することを保証しているクラス a は、所謂、内包的定義で、
{x | F}
と書くもののことなのである。
つまり、区間 (0,1) を、{x | 0<x<1}と定義するが、そのように定義された集合が存在するというのが、この公理が主張していることなのである。
ラッセルは、この公理が存在を保証するクラスのみから全数学を再構築することに成功したのである。
それを、例えば自然数の場合にやってみよう。
たとえば自然数の1を作ってみよう。
ラッセルは、自然数1を、特称名辞のように、対象が一つしか入ってないクラスすべてのクラスとして定義した。
類aに対象がちょうど一つしかないということは、現代的な述語論理学の記号を使うと、
∃x.(x∈a)∧∀x.∀y.(x∈a∧y∈a→x=y)
と書く。
これの内容は、
x∈aとなる x がある、かつ、どんな x, y に対しても(x∈aかつy∈aならばx=yである)
という意味である。つまり、a はすくなくとも要素を一つはもっていて、しかも、もし、x, y が両方とも a の要素ならば、実は同じものだ、ということである。
確かに、これで要素がひとつだけという条件が表現されていることがわかるだろう。
これを使うと、数1というのは、
{a| Class(a)∧∃x.(x∈a)∧∀x.∀y.(x∈a∧y∈a→x=y)}
というクラスとして定義できる。
このクラスをOneと書くとする。
sが、要素が丁度ひとつのクラスであることが、s∈One と書ける。
同じテクニックで、2は、要素の数が丁度二つの類を全部集めた類として、3は、要素の数が丁度三つの類を全部集めた類として定義できることが分かるだろう。
たとえば、2は、
a には、x, y という要素があり、かつ、x=y ではない。また、a の任意の要素 z は、z=x かz=y となる、
という文章を論理式Gにして、それを満たす、すべてのクラスの全体{a | G} を Two とすればよい。
そうすると、sが、要素が丁度ひとつのクラスであることが、s∈Two と書ける。
大変、手間はかかるが、このようにして、整数、有理数、実数、複素数などすべての数作っていくことができるのである。
そして、数の世界を創造すると、それを利用した幾何の空間も創造すうことができた。(座標を使う)
そしてラッセルが、The Principles of Mathematics 、§ 4に書いたように、これから生まれてくるだろう数学の概念も、この仕組みだけを使って作れるだろうという、確かな手ごたえがあったのである。
ラッセルの論理学を使えば、全数学が再構築できる。
この様な、「数学は論理学に還元できる」「数学は論理学の一部である」というような立場を、論理主義という。
数学的真理は、すべて論理的に導出できるのか、というような問題は、カントの様な哲学者が考える問題である。
それを、数学の論理学への応用である数理論理学を使って解決するというのが、論理主義なのである。
カントやデカルトなどは、数学には直観のようなものが欠かせないとしたが、ラッセルは、そうではないというのである。
これは、当然、哲学に大きなインパクトを持つ発見であった。
このラッセルの論理主義を受けて、哲学界は、大きく転換していくことになる。
話を数学に戻すと、実は、この論理主義を、数理論理学なしで実行した人がいた。
それが、講義の最初のころに出て来たデーデキントである。
上で説明した、ラッセルの自然数の作り方が、デーデキントの切断やイデアルの発想によく似ていることはわかると思う。
実は、デーデキントは、ラッセルやペアノより前の、1888年の著書 Was sind und was sollen die Zahlen? で、
実数などが、自然数に還元できたが、自然数は、それより簡単な数学的概念がないので、
論理学に還元するしかないとして、それを実行してみせたのである。
この時、まだ、ペアノの論理学はなく、また、デーデキントが、第二版で、出版後に、Schröder の仕事を知ったと書いている。
フレーゲの論理学はあったのだが、デーデキントは知らなかったようである。
では、デーデキントは何を使ったかというと、それは彼流に改変された伝統的論理学であったのである。
このデーデキントの「論理学」は、今からみれば、むしろ集合論に見えるものであるが、
たとえば、ソクラテスと、ソクラテスの集合を混同して使うという伝統的論理学の特長をもっていた。(たとえば、この本の八杉・林の稿を参照)
この伝統的な混同は、Schröder の論理学でも継承されており、この二人が、まだ、伝統論理学の枠の上で思考していたことがわかる。
この二つの分離の必要性が、広く認識されるようになるにはペアノの論理学を待たねばならなかったのである。
ちなみに、先に述べたフレーゲへのペアノのコンタクトで、ペアノからの便りへの返信で、
フレーゲは、ペアノが、∈と⊂を分離したことを称え、ほとんどの学者はこれを混同している、たとえば、デーデキント氏がそうだ、と書いている。(上掲Kennedyによる伝記より)
デーデキントの論理主義のもうひとつの特長は、デーデキントが、ラッセルと違い、自然数を内包の公理のみで構築しなかったことである。
デーデキントの自然数の作り方は、ラッセルのものがカントルの超限基数論的であったのに対し、超限順序数論的であった。
そして、デーデキントは、自然数構築の出発点として、人間が思考しえるもの全部の集合(彼は、集合と呼ばず、System と呼んでいる。これもリーマンが講義の際に集合の意味で使っていた言葉である)を使っている。
ある a を思考するということは、a そのものではなく、しかし、また、思考しえるものである、ということから、彼は、この集合が、その真部分集合と一対一に対応すると主張し、そこから自然数を構築したのである。
これは、明らかに哲学的議論であり、現代から見れば数学の理論の中で使うのは非常に不適切である。
しかし、自然数の概念を伝統的論理学の亜種に還元するというデーデキントの主張からすれば、
そして、論理学が哲学の一部であることを考えれば、こういう議論が数学書の中で使われることは、
デーデキントにとっては、許容できることだったのだろう。
以上の説明だけを読めば、これで数学の基礎の問題は、すべて解消すると思えるかもしれない。
実際、ラッセルの1903年の著書は、そのようなトーンで書かれていた。
しかし、同時に、その本には、The Contradiction と題されたチャプタが存在したのである。
実は、ラッセルは、彼の論理学の開拓のかなり早い時期に、彼の理論に、大きな問題があることを発見していたのである。
しかし、それは、何かの方法で解決できるはずだと信じ、前に進んだ、そして、書かれたのが、1903年の著書だったのである。
その問題が、現在、ラッセルのパラドックスと呼ばれるものである。
ラッセルは、このころすでにドイツの若い数学者たちを中心にして、市民権を得るようになった、カントールの集合論を研究しており、
それを通して、以前、説明したカントールの定理を知っていた。
どんな集合に対しても、その冪集合の方が要素が多い、つまり、その間に一対一対応は作れないという定理である。
しかし、ラッセルは、この定理には何か間違いがあると感じた。
というのは、カントールの超限基数全体が、一つの超限基数を生むので、それが最大の超限基数となるはずだ、
つまり、無限集合の要素の数には、最大のものがあるはずだと思ったからである。
これは、それより前、1896年頃に、カントール自身が発見していたことなのだが、恐らくは、ラッセルは自分自身で発見したと思われる。
注. カントール自身は、これを超限基数全体は、矛盾した集合であるというポジティブな結果と理解していた。彼は、集合を矛盾したものと、無矛盾なものとに分類して考えていたのである。
ラッセルは、今や、数学の概念構成や推論を、彼の数理論理学で精密に行うことができた。
その代数計算のような精密な推論方法を使えば、カントールの証明の間違いを発見できると考えたらしい。
しかし、その分析によって、彼が発見したのは、彼の考え方からしたら、純粋に論理学的矛盾だったのである。
先に示したカントールの定理の証明から、このラッセルの矛盾を作りだしてみよう。
まず、カントールの定理の証明を再録する。
---------------------------
背理法で証明する。
AとPow(A)の間に一対一対応 f :A→ Pow(A) があるとする。
集合Rを
R={x∈A|x∉f(x)}
と定義する。これはPow(A)の要素である。
fは一対一対応なので、f(a)=R となる a をとれる。つまり、
a∈Aを
f(a)={x∈A|x∉f(x)}
となるものとする。
そのとき、
a∈f(a) ⇔ a∈{x∈A|x∉f(x)} ⇔ a∉f(a)
となるので、これは矛盾である。
よって、この様な一対一対応fは存在しない。
---------------------------
これの一部を赤字にする。
---------------------------
背理法で証明する。
AとPow(A)の間に一対一対応 f :A→ Pow(A) があるとする。
集合Rを
R={x∈A|x∉f(x)}
と定義する。これはPow(A)の要素である。
fは一対一対応なので、f(a)=R となる a をとれる。つまり、
a∈Aを
f(a)={x∈A|x∉f(x)}
となるものとする。
そのとき、
a∈f(a) ⇔ a∈{x∈A|x∉f(x)} ⇔ a∉f(a)
となるので、これは矛盾である。
よって、この様な一対一対応fは存在しない。
---------------------------
この赤字の部分を消す。
---------------------------
集合Rを
R={x|x∉x}
と定義する。
a=R となる a をとれる。
そのとき、
a∈a ⇔ a∈{x|x∉x} ⇔ a∉a
となるので、これは矛盾である。
---------------------------
「a=R となる a をとれる」は変な文章だが、要するに、aをRとするという意味である。
だから、a にRを代入して、次のように言い変えられる。
---------------------------
集合Rを
R={x|x∉x}
と定義する。
そのとき、
R∈R ⇔ R∈{x|x∉x} ⇔ R∉R
となるので、これは矛盾である。
---------------------------
この証明は、ラッセルの論理学で正しいとされる証明であった。
そして、これにはカントールの定理と違い、背理法の前提がない。
つまり、ラッセルの論理学は、矛盾を含んでいたのである。
実は、同じような集合論の矛盾は、ペアノ学派によっても超限順序数に対して発見されていたのである。
しかし、ラッセルの矛盾が発見されるまで、それやカントールの発見したものは、
ラッセルが、最初、そう思ったように、根本的な問題だとは認識されなかったのである。
しかし、このある意味で、「純化された矛盾」により、これ以後、数学界と哲学界は、大混乱と大発展をすることとなる。
それが後期の話となる。
終