シラバスにある「ツェルメロのパラドックスとゲッチンゲン」は、後期の講義にまわし、前期には触れません。
無限集合は、有限集合にない不思議な性質を持つ。
そのいくつかは、古くから知られており、例えば、有名な所では、ガリレオ・ガリレイの「新科学対話」にある所謂「ガリレオのパラドックス」という次の様なものがある。(現代の言葉を使って書いてある。ガリレオが「集合」などと書いているのではない。)
正整数を2乗してできる数を、平方数という。つまり、1, 4, 9, 16, 25,..... である。しかし、2, 3, 5, 7, 8,.... などは平方数ではないので、平方数の全体は、正整数の全体の、それより本当に小さい一部分である。
それにも関わらず、総ての正整数1, 2, 3, 4, 5, ..の集合と、総ての平方数1, 4, 9, 16, 25,..... の集合は、12=1, 22=4, 32=9,.... のように一対一に対応する。
25までの25個の数からなる集合{1,2,..., 25}に限定すると、その平方数の集合{1, 4, 9, 16, 25}は、{1,2,..., 25}の、それより本当に小さい一部分、いわゆる真部分集合である。
25までの平方数の集合{1, 4, 9, 16, 25}は5個しか要素がないので、要素が25個ある集合{1,2,..., 25}との間に一対一対応はない。
この様に、有限集合ならば、その真部分集合との間に一対一対応がないことは明らかである。
しかし、無限集合では、その真部分集合で、元の無限集合と一対一対応がつくものが必ず存在するのである。
最初、解析学への応用のために複雑な無限集合を考えていたカントルだが、段々と、この様な有限集合と大きく異なる無限集合の不思議な性質そのものに興味を惹かれるようなり、純粋集合論とでもよぶべき、「集合論のための集合論」を探究していった。もちろん、それはベルリン流の堅実な数学からすると、まったくの異端だった。
最初の重要な発見は、1873年11月29日のデーデキントへの手紙で提起した、自然数の集合と実数の集合の間に一対一対応があるかという問題の解決で、1873年12月7日のことであった。
自然数と一対一対応する集合を可算集合というので、これは実数の全体の集合は非可算集合だということである。
自然数の集合は実数の集合の部分集合だから、これは実数は自然数より、ずっと沢山あるという結果でもあった。
そして、この事実の簡単な応用として、「超越数が存在する」という有名な定理の非常に短い別証明を導くことができた。
超越数というのは、実数で、6月5日の資料で説明した代数的数でないもののことを言う。
代数的数が可算であることは比較的簡単に示せるので、実数が非可算であれば、当然、超越数が存在することになるのである。
超越数が存在することは、19世紀半ばに初めて証明されたが、カントルの証明は、それより遥かに簡単だった。
この当時、超越数の研究のテーマは、特定の数、例えば円周率πが超越数であることを示すことに移っていたので、カントルの示した結果は、数学的には重要なものとは言えなかった。
それでも、これは数学の伝統的問題への貢献があったので、例えばワイエルシュトラスは、これを評価して出版を勧めている。
しかし、円周率πが超越数であることを証明したリンデマンに、「あなたの円周率についての美しい研究は何の役にたつのか?無理数というものが存在しないのに、どうしてそういうことのを考えるのか?」と言ったとされるクロネッカーは、当然、カントルの仕事を高く評価するようなことはなかったと思われる。
注.この逸話は、リンデマン自身が記録したものだが、クロネッカーの研究で知られる米国の数学史家、エドワーズは、クロネッカーがその通りに行ったはずはないとしている。実際、クロネッカーは円周率を彼の研究や講義で使っているし、それが超越数であることも講義中に述べていることをエドワーズは指摘している。また、無理数√2などは、代数的数なので、クロネッカーやクンマーの数学では自然な存在なので、そのことからも、クロネッカーが、この様に言ったとしたら変である。しかし、クロネッカーが、デーデキントやカントルのような「実数の定義」のようなものを無意味だと思っていたことは確かの様であり、リンデマンの様な研究の方向性を、あまり意味がないものとして考えていた可能性はある。(詳しくは、H.M.Edwards, Essays in Constructive Mathematics, Essay 5.5 を参照)
そのためか、カントルは、自らが属するベルリン学派の数学者ではなく、ゲッチンゲン学派の数学者デーデキントに自分の発見を書簡で報告しながら、集合の理論を開拓していった。
その中で、カントル自身にとって、エポックメイキングだったと言われているのが、平面の点と直線の点の間に一対一対応があることの発見だったと言われる。これは1877年のことであり、出版されたのは翌年である。
カントルは、この様なことはないと信じていたので、自身の発見に驚き、デーデキントに自らの発見について意見を求める手紙を書いた際に、フランス語で「私は見るが、信じない」と書いたことは有名である。
実数直線は、二次元平面の中の、ほんの一部なので、カントルの驚きはもっともといえる。
ただし、カントルは驚いたが、これは分かってみれば簡単に証明できる。細かい点で工夫が必要だが、簡単に言えば、0.123456.... という無限小数は、奇数桁だけとると、0.135.... 、偶数桁だけとると0.246.... という二つの数に「分解」できる。それぞれを、x, y とすると、これは、平面の点の座標 (x,y) だと見なせる。この対応により、実数と実数の対の集合の間に1対1対応をつくれるのである。
このな風な、一見パズルの様な工夫を使いながら、カントルは彼の集合の理論を構築していった。それは、それまでの数学とあまりに違うものだったので、多くの数学者が、胡散臭いものと考えたのは無理もなかったであろう。
集合論が数学の基礎として定着した現在でも、これに違和感を唱える数学者は後を絶たない。確かに、それは数学の伝統からは、あまりに乖離したものだったのである。
注. そして、逆に、それが集合論やカントルが数学の一般向け書籍で持てはやされる理由にもなっている。そのため、集合論や、これから説明する記号論理学、そして、それらによる数学の基礎に対する態度が、幾何、代数、解析のような伝統的分野の数学者とそうでない人たちの間で、大変に違う原因となっている。数学の主流は、現在でも、幾何、代数、解析にルーツを持つ諸分野であるが、哲学者などは、この事実を見落としがちで、数学に対する間違ったイメージを持つ人が大半で、それが哲学者と数学者の意思疎通を妨げている。
1877年に「私は見るが、信じない」と書き送ったころのカントルは、n次元平面を「n 次元連続多様体」 eine stetige Mannigfaltigkeit von n Dimensionen と呼んでおり、リーマンの影響が用語に見て取れる。
また、このころのカントルは、リーマンの幾何学に興味をもっており、自分の集合論の研究と、それを結び付けて考えていたことが、デーデキントとの間の書簡の分析で分かっている。(Ferreiros Chap. VI, 4.3)
このリーマンの数学への注目がシンボライズするように、カントルは、平面と直線の一対一対応など、新規な発見を続けることにより、段々とベルリン数学の正統から逸脱していった。
それに従いベルリンの数学者たちは、カントルの数学を異端視するようになり、たとえば、当時、非常に評価が高かったクレレ・ジャーナルと呼ばれる専門誌の編集をおこなっていたクロネッカーは、カントルの集合論関係の論文を、この雑誌から排除するようになっていった。
このカントルとクロネッカーの対立は、アメリカの数学者兼小説家のE.T.ベルがベストセラーの数学読み物「数学をつくった人びと」で、二人の対立を面白おかしく取り上げたことで、良く知られているが、実は、このベルのストーリーは大半が嘘である。カントルとクロネッカーの話だけでなく、「数学をつくった人びと」の他の数学者たちのストーリーも、殆どベルの創作と言えたので、数学史家や数学者からの厳しい批判を浴びている。
このクロネッカーとカントルの対立がどんなものだったのかは、今ではかなり詳細にわかっている。この対立は哲学的なもの、あるいは、数学はどうあるべきかという数学論的なものであった。しかし、これに並行して、デーデキントとクロネッカー・クンマーの「対立」が起きており、これは数学論的なものもあったが、数学上の対立の要素の方が大きかった。
この二つの対立は、後期の2も含めて、この講義の重要なポイントとなるのだが、海の日の休みを計算に入れていなかったために時間が不足気味なので、これは後期の講義で扱うこととする。
さて、話を戻して、この様なベルリン学派からの逸脱による孤立の状況を支えたのは、デーデキントの存在が大きかったと思われる。
ここまで説明して来た様に、カントルは、自分でも「見るが信じられない」純粋集合論の緒結果を、常にデーデキントに書簡で知らせ、あまりに当時の数学の手法から逸脱していたために、彼自身にも不安が残った、それらの結果の証明の「正しさ」についてデーデキントの意見を聞いている。これがカントルの集合論の開拓の大きな支えになったのは言うまでもないだろう。
しかし、このデーデキントとの関係も、やがて終わりを迎える。
実は、カントル集合論の最初の成果と言えた、超越数の存在の別証明の発見の際、代数的数が可算であることを最初に発見したのはデーデキントだったと思われるのである。少なくとも、二人の書簡中に、それが現れるのは、デーデキントからカントルへの書簡の一つなのである。しかし、カントルは、それを論文にする時、デーデキントが、それを発見したことを書かなかった。
デーデキントは、大変に控え目で争いをさける人だったことが知られているが、それもあってデーデキントが、このことでカントルを問い詰めることはなかったが、後にカントルが、「理由はわからないが、どもデーデキントは自分に対して怒りの感情をもっているようだ」と、ある手紙に書いているように、実際にはデーデキントはカントルに対して複雑な感情を持っていたようである。
実はカントルは、幼少のころから精神的に不安定だったといわれ、1884年には、精神病を発症し、以後、死去するまで、発病と回復を繰り返した。この時期は、1884年5月の最初の発病以前であるが、行動に普通ではない所があったとしても不思議ではない。その「異常性」が、カントルの集合論という、それまでの数学から逸脱したものの開拓に寄与したという人もいるが、その高く空中を飛翔するかのような思考と性格は、常識人中の常識人で堅実そのものだったデーデキントと、反りが合わなくなるのは必然だったのかもしれない。
この両者の関係の悪化が顕在化するのは、1881年にハイネの死去により、空席になったハレ大学の教授職にカントルがデーデキントを招請しようとしたのに対し、デーデキントがこれを断った頃からだともいわれる。Ferreirosは、これをクロネッカーとの対立などでベルリン学派から孤立したカントルが、デーデキントに支えを求めたのだろうとしている。しかし、デーデキントは、それを断ったのである。(Ferreiros VI, 5)
デーデキントは、現在は、工科大学となっているブラウンシュヴァイクの工業学校の教師として一生を過ごした。現在は、世界有数の大学である、チューリッヒ工科大学で解析学を教えた時、切断の概念を発見したことは、すでに述べたが、この時は、チューリッヒ工科大学は、まだ、新設の工業学校であり大学ではなかった。19世紀には、工学は大学で教えるような学問と見なされていなかったからである。
つまり、デーデキントは、一度も大学の教師だったことは無かったのである。偉大な数学者としては、珍しいことである。学者というものは、カントルが特にそうであったように、評価の高い大学や研究機関に在職するためには、例えば日本では単身赴任をしたりして家庭を犠牲にするのことの方が多い。
しかし、デーデキントは、そういうカントルや多くの学者とは、全く違った人物だった。彼が在職した工業学校は、彼の生地にあり、また、彼の父が運営していた学校でもある。彼は一生独身を通したが、妹などの新族がブラウンシュヴァイクにいた。また、給与も悪くなかったようだし、学校のいわゆる雑事も積極的にこなしたようである。それらのことから、デーデキントは、充実した人生に満足していたようで、大学に職を求める気はなかったようなのである。
これは、ベルリン大学の教授職を渇望するなど、常に評価に飢え、精神的に苦しんだカントルと大きな対照をなす。この二人ほど対照的な人物たちが、集合論の草創期に重要な役割をしたことは非常に面白い事実である。
そして、それは二人の集合論への関わり方にも現れていた。その話は、この講義でいう現代の数学の基礎への4ルート(幾何・代数を統合して考えれば3ルート)の最後の一つである論理学ルートの際に説明する。そして、今は、その論理学ルートの立役者である哲学者バートランド・ラッセルの論理学による数学の基礎づけ研究につながり、この後の数学の基礎の歴史に大きな影響を与えることになった、カントルの超限数の理論について説明しよう。
カントルの集合論研究を支えた、デーデキントとの書簡のやり取りは1882年にカントールが書き送った書簡をデーデキントが無視して返事を送らなかったときに終わった。そして、その書簡で導入されていたのが、この超限数の理論だったのである。(Ferreiros, p.201)
「論理学ルート」の解説で説明するように、デーデキントの集合論は、数学を厳密に基礎づけるということに力点があった。そのため、彼は実数、理想数に続いて、自然数を基礎づけるということまでしているが、カントルの態度は、まったく逆だった。
カントルは、ベルリン学派の中に留まっていたころは、三角級数の研究のための必要性から、実数を厳密に定義すると言う様なことをしていたが、ベルリン学派から逸脱し、集合論の翼を得て高く飛翔するようになるに従い、以前紹介した、Schwartz の言い方を借りれば、数学ロマンチスト、数学詩人の「想像の産物」を次々と考え出した。
その最大のもので、現代も純粋集合論の最も重要な概念であるものが、超限数の理論である。
先に、一対一対応により、有限集合の「要素の多さ」を比較できることを、運動会の玉入れの譬えを使って説明した。これは口頭で説明しただけで、資料には書いてないので、ここで記録すると次のようになる:
運動会の玉入れで、白組が勝ったか、紅組が勝ったかを判定するために、ひとつ、ふたつ、…と数えながら、篭から玉をひとつずつとりあげて外に放り出す。そうして、紅組の玉が早く尽きれば赤の玉の方がすくないのだから、紅組の負け、白組の玉が先に尽きれば白組の負けである。そして、もし、同時に篭の中の玉が尽きれば、両者の玉の数は同じなのだから、引き分けとなる。この引き分けの場合が、赤い玉の集合と白い玉の集合に一対一対応がついた場合である。
この一対一対応をとるには、「ひとつ、ふたつ、…」と数を使って数える必要はない。だから、数の概念がなくても集合の「要素の数」を「同数」かどうか判定できる。そのために、数えることができない無限集合、たとえば、自然数の集合や、実数の集合、平面の点の集合の「要素の数の比較」ができたのだった。
しかし、カントルは、1882年、この考え方を反転させて、無限集合の個数を表す超限基数というものを導入した。そして、それに関連して超限り順序数というものも導入した。つまり、無限の数を考えたのである。
これの理論的構成の詳細の説明は省くが、その理論の大雑把な構造を説明しよう。
そして、カントルは、これらの無限の数にたいして、和や積などを定義し、その性質を研究した。
平面は直線の点の対、つまり、座標(x,y)の集まりと見なせるが、この様な対(座標)の集合を直積集合といい、有限集合の場合は、対の要素をとってくる集合の個数の積がだけ要素があることがわかる。
それでカントルは、この直積集合の個数も、もとの二つの集合の個数の積と定めた。
実数の集合の基数をℵと書くが、平面と直線の間に一対一対応があるという結果は、要するにℵ×ℵ=ℵという事実を表しているのである。
実は、有限の数の場合には、0と1以外ではなりたたない、a×a= a というこの等式は、無限の基数の場合には必ず成り立つのである。
カントルは、このような不思議な定理を、超限基数、超限順序数双方で、次々と発見し証明していった。
しかし、カントルは、二つの重要な定理を成り立つと予想しながら、どうしても証明できなかった。
それが、次の二つであった:
カントルは、この二つの定理を証明できなかったものの、殆ど独力で、無限の理論である、純粋集合論を開拓していった。
カントルが開拓した純粋集合論では、当然ながら、超限基数と超限順序数の様な新しい概念を導入されると同時に、数々の定理が証明された。
その中で、特に「カントルの定理」と呼ばれている有名な定理がある。
これから、どんな集合でも、それより数の多い要素をもつ集合があるということが分かるので、超限基数論の言葉でいえば、「最大の超限基数はない」という事実がわかる。
aが A の要素ならば、{a} という集合は Pow(A) の要素なので、Pow(A) の方が、Aより以上の要素をもつ。
しかし、同数であることはない。つまり、AとPow(A)の間には、一対一対応はない、というのがこの定理である。
それの証明は、非常に簡単だが、対角線論法という面白い議論を使うので有名である。
しかし、この対角線論法が、厄介な問題を引き起こしてしまったのである。
証明は簡単なので、紹介しておこう。
背理法で証明する。
AとPow(A)の間に一対一対応 f :A→ Pow(A) があるとする。つまり、x∈A ならば f(x)∈Pow(A) である。
集合Rを
R={x∈A|x∉f(x)}
と定義する。これはPow(A)の要素である。
fは一対一対応なので、f(a)=R となる a をとれる。つまり、
a∈Aを
f(a)={x∈A|x∉f(x)}
となるものとする。
そのとき、
a∈f(a) ⇔ a∈{x∈A|x∉f(x)} ⇔ a∉f(a)
となるので、これは矛盾である。
よって、この様な一対一対応fは存在しない。
この定理を、論理学ルートの立役者、バートランド・ラッセルは、間違いだと考えた。
その理由は、超限基数全体の集合の基数は、最大の超限基数となるはずだと考えたからである。
この事実は、ラッセル以前にカントルが気が付いているが、カントルは、これは集合には、矛盾したものと矛盾しないものがあるということの証明だと考えた。
この二人が気が付いた事実を、今では「カントルのパラドックス」という。
この奇妙な事態を、ラッセルは、彼の記号論理学で解決しようとし、さらに厄介な世界に踏み込んでしまうことになった。
数学の新基礎となるべき集合論、そして、ギリシャ以来の論理学が破綻してしまったのである。
ラッセル・パラドックスの発見である。
この話をするために、次の論理学ルートについて説明する。
今までの話の登場人物は、すべて数学者であった。
リーマンが自信を自然哲学者と考える哲学的傾向が強い人であったと言われるものの、
また、そのリーマンやカントルの理論が、当時のベルリン学派の立場からは、数学から逸脱しているものであったものの、
そして、カントルが、その様な自分の理論を哲学、さらには神学と結び付けて考えるようになったものの、
総ては数学者が、数学的目的で考え出したものである。
たとえば、集合論を神学にさえ関係づけたカントルも、集合論研究の最初の動機は、如何にも数学者らしい、
知的好奇心からであったことは、以上に述べた歴史から明らかである。
しかし、ここからの話は大きく異なる。
登場人物の多くは、哲学者や哲学と数学の境界で仕事をした人、あるいは、哲学の一分野である論理学に数学を応用しようとした人たちである。
つまり、ここからの話は、哲学ルートと言っても良いのである。
その哲学ルートが、このルートの立役者である哲学者バートランド・ラッセルにより、
古代ギリシャ以来の論理学が、数学と統合され、数理論理学、記号論理学
というものが誕生することにより、むしろ数学の一部に吸収されることとなり、
数学の近代的基礎が誕生するのである。
この最後の課程は、後期の講義で話すことになるが、前期では、
ラッセルが、論理学による数学の基礎づけ、所謂、論理主義というものを生み出し、
それにより数学の基礎を堅固にしようとしたが、カントルの定理のために、
ラッセルのパラドックスと呼ばれるものを発見して、
むしろ、数学と論理学の基礎を同時に破壊してしまったという話まで進む。
古い歴史観ならば、ここで19世紀における 数理論理学、記号論理学の発展の話から
始めるところだが、この講義では、Ferreiros に従い、この背景にある、
アリストテレス論理学、いわゆる、伝統的論理学から始める。
19世紀には、というよりラッセウが状況を変えてしまう、20世紀の初めころまでは、
論理学とは、伝統的論理学、アリストテレス論理学のことであったのである。
名辞は、英語では term といい、だから、アリストテレス論理学は、英語では term logic という。
名辞は、非常に大雑把に言えば名詞、あるいは、名詞とそれが指し示すものを合わせたものと思っておけばよい。
たとえば、
などが名辞である。例が大げさだが、これは昨年度までやっていた論理学の歴史という講義で使っていた、明治の論理学書から引用しているからである。
1のような名辞は固有名詞に対応する。つまり、指し示すものが一つである。2の様なものは多くのものを指す。
その意味でかなり性格が違い、英語で言えば単数形と複数形の違いがあるのだが、これを名辞論理学では、同じ名辞として扱う。
1の方は、英語では singular term、2は universal term という。日本語には、現在定着した訳語がないようだが、昨年まで使っていた明治の教科書では、特称名辞、通称名辞と呼ばれている。
この様な名辞を組み合わせてできるのが、次の命題である。
命題というのは意味を持つ文章のことだと思っておけばよい。
アリストテレス論理学では、命題の基本単位は、二つの名辞から作られる
A be B
という形であると考える。ここで、A と B が名辞。
たとえば、次のものはみなそういう形をしている。
孟子 is 人
孟子 is 中国人
孟子 is 学者
中国人 are 人
学者 are 人
以上は皆正しいもの。
しかし、
中国人 are 孟子
人 are 学者
は間違いである。
この A be B のような形の基本形の命題は、categorical proposition と呼ばれている。(現在定着した日本語訳はないようである)
この様に名辞を結ぶ be を コピュラ、copula、 繋辞(けいじ)、連辞(れんじ)といい、
A be B のAを主語、Bを述語という。
ここまでで、すでに分かったと思うが、アリストテレス論理学は、英語やドイツ語、ラテン語などの言語の構造に根ざしている所があり、例えば、英語を使うと説明しやすいが、日本語に例えて説明すると不自然になる。
そこで、以下では、経済学者 John Maynard Keynes の父である John Neville Keynes の論理学の教科書を使って、英語に引き当ててアリストテレス論理学を説明していく。
これが Keynes の教科書、Studies and Exercises in Formal Logic の第2版の、該当部分。Internet Archive 版
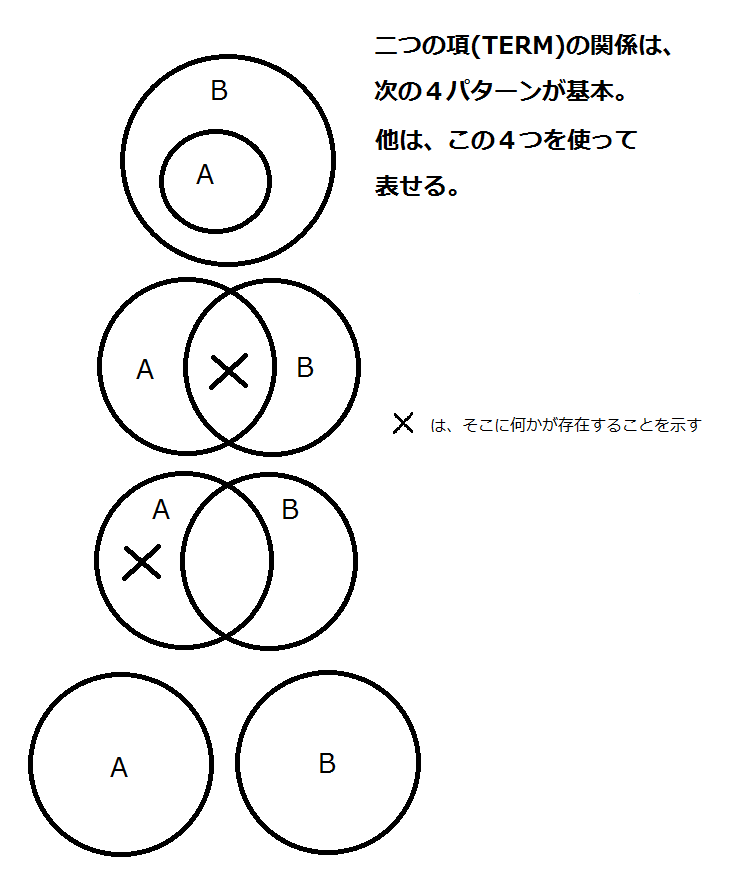
名辞を集合だと思うと、基本的には、二つの名辞の関係性には、対称的なものを同一視すると、次の4パターンしかないことがわかる。

他にもありそうな気が…
しかし、良く考えてみると、二つの名辞の関係は、本質的にはこの4パターンに還元できることがわかる。
たとえば、
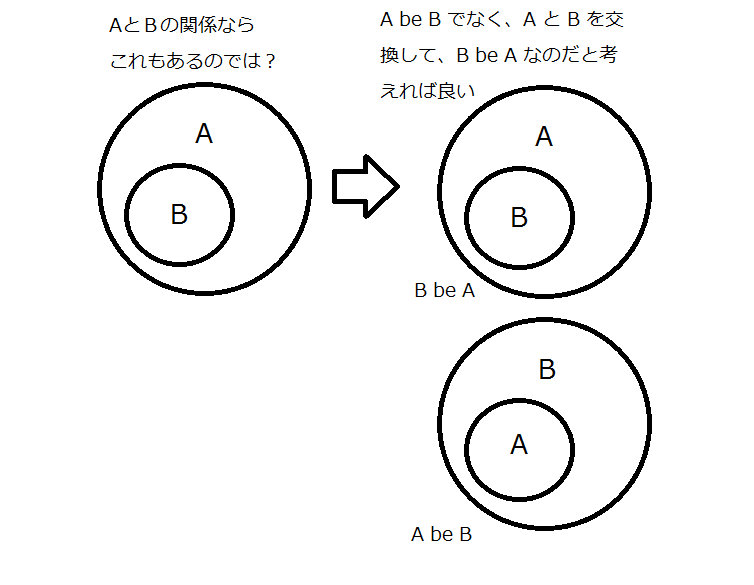
さらに…
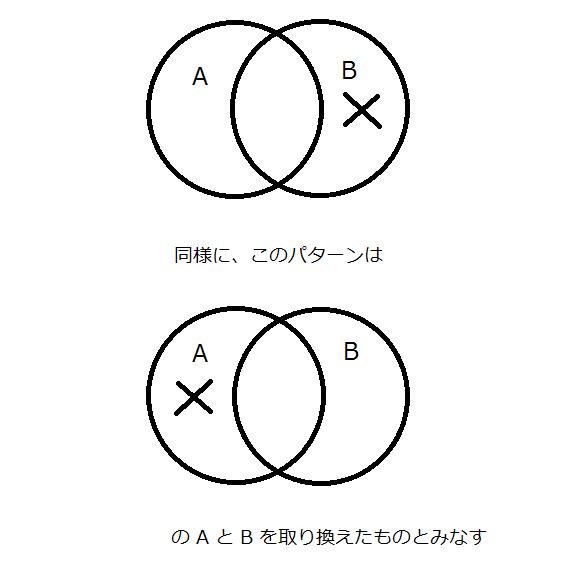
もうひとつ…
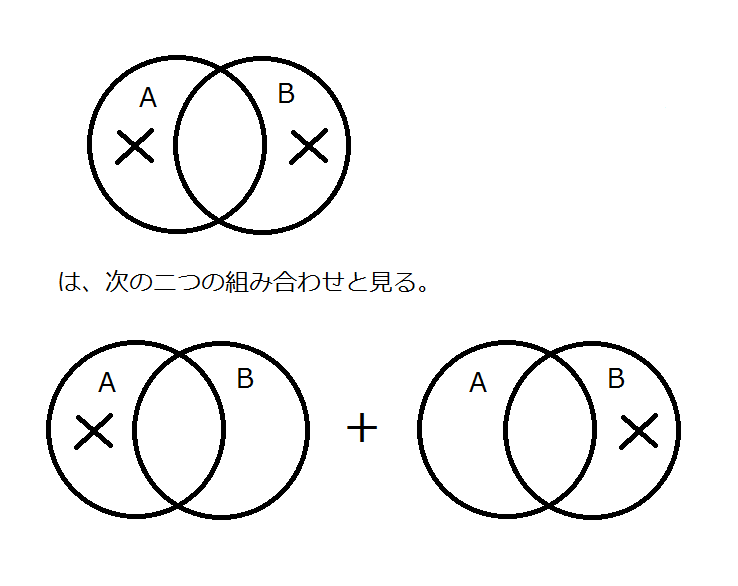
Keynes の教科書を参照すること
Categorical proposition には、次のAEIOの四つの型がある。
各型の正式名称は、「全称肯定」などで、記号と書いているA,E,I,Oが、型の名前の省略記号である。
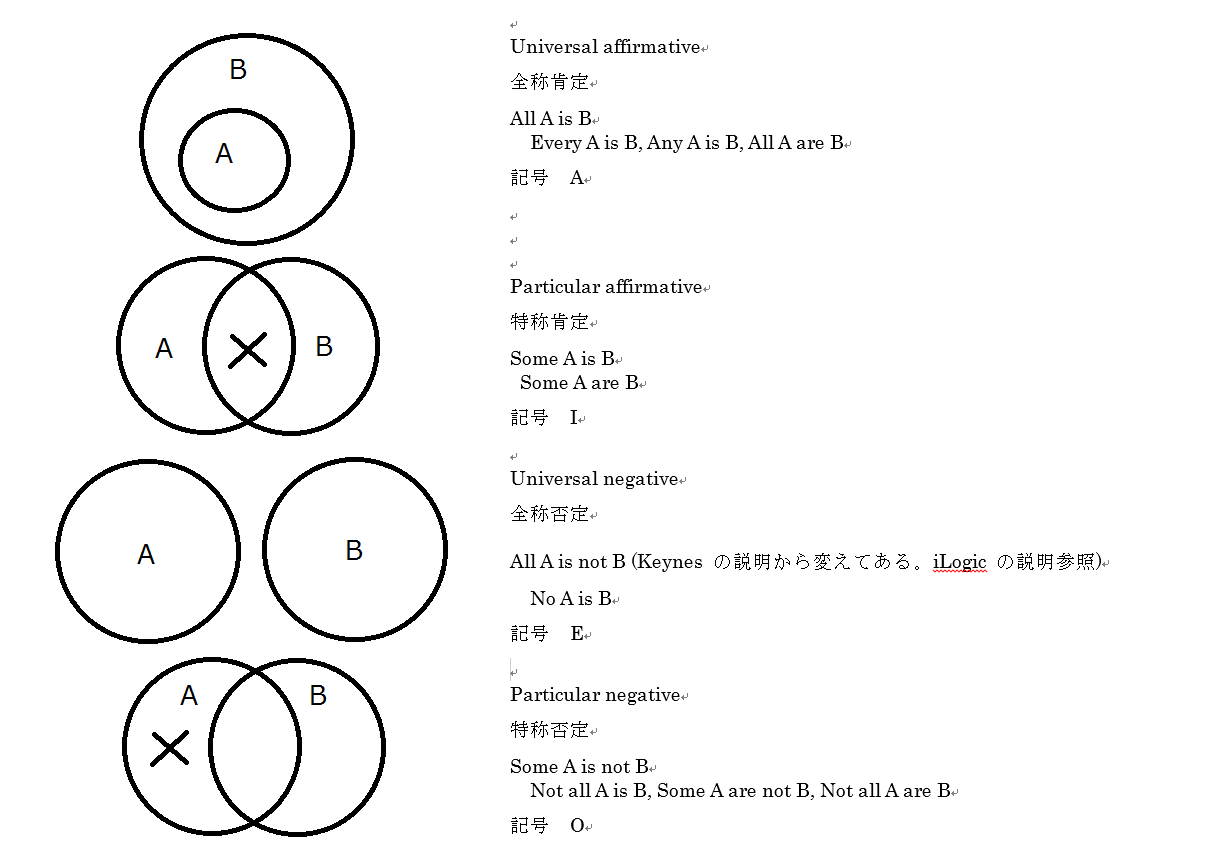
アリストテレス論理学の本体部分は、推論(正確には演繹)について論じるシロギズム、三段論法の理論である。
論理学と言えば、有名な三段論法
が引き合いに出される。
この様な演繹(推論)の正しさを体系づけたものが、三段論法の理論、シロギズムである。
アリストテレス論理学の説明の最後に、これを解説する。
上記の三段論法の、人間、死ぬもの、はどちらも名辞であり、2の「人間は死ぬものである」は、典型的なA型(AEIOのAということ)の命題、つまり、全称肯定命題である。
では、1の「ソクラテスは人間である」と「ソクラテスは死ぬものである」はどの様に考えるべきだろうか。
文章の形から、あきらかに、A be B の、A という主語の名辞は、「ソクラテス」である。
しかし、「ソクラテス」は、一人の人を表す項であり、「人間」とか「死ぬもの」などの集団を表す項とは違うようにみえる。
実は、ここにアリストテレス論理学の大きな特徴がある。
5月1日の資料で、高校数学の集合の定義の説明で使われる、外延、内包という言葉のルーツの説明をした。
再録すると、次の様になる(アリストレス論理学のルーツといえるポール・ロワイヤル論理学の英訳から):
Now, in these universal ideas there are two things, which it is very important accurately to distinguish COMPREHENSION and EXTENSION. I call the COMPREHENSION of an idea, those attributes which it involves in itself, and which cannot be taken away from it without destroying it; as the comprehension of the idea triangle includes extension, figure, three lines, three angles, and the equality of these three angles to two right angles, &c.
I call the EXTENSION of an idea those subjects to which that idea applies, which are also called the inferiors of a general term, which, in relation to them, is called superior, as the idea of triangle in general extends to all the different sorts of triangles.
ここではtriangle 三角形という term の内包と外延が説明されている。外延 Extension の方は簡単で、すべての三角形の全体、つまり、三角形の集合ということで、現代的な「外延的定義」、つまり、三角形全部を並べあげる定義と意図が一致する。
内包 Comprehension というのは名辞の「本質」のようなもので、これを説明するのは難しい。
実際、これの説明は、色々なアリストレス論理学の本を見ると、それぞれ微妙に異なる。
「本質」のような哲学的な概念を、スッキリ説明することは困難なのである。
一方で、外延は、集合という概念を理解していれば簡単である。
「三角形」 "triangle" という名辞の概念は、それが指し示すもの全体、つまり、三角形と呼ばれるものの集合なのである。
これが集合だから、上に説明した categorical proposition の4つの型 AEIO を、集合の図(ベン図)を使って説明できたのである。
つまり、このAEIOの説明では、どのような名辞も、その属性 attribute の一つとして外延とよばれる集合を持っていることになる。
上のComprehension 内包の説明で三角形の内包の説明で、"as the comprehension of the idea triangle includes extension, figure, ..." と、先頭に書かれているように、
これは名辞の使われ方を完全に説明するもので、数々ある内包の属性の内でも最も重要なものとも考えられる。
実際、a be Triangle という categorical propositon の真偽を知るには、Triangle の外延だけあればよい。その意味で外延は、名辞の本質の大半を担うものといえる。
注.この説明と、クンマーの理想数とデーデキントのイデアルと切断の説明は似ている。その意味を考えてみて欲しい。
実は、この外延のみを独立させて、厄介な「内包」を、高校数学で行うように外延(集合)の定義を行う時に使うものと限定したものが、現代の集合概念だと考えることができる。
いずれにせよ、アリストテレス論理学では、「ソクラテス」という名辞の外延は、集合のような、ものの集まりということになる。
それは「固有名詞」なのだがら、当然、集合の要素の数は一つでないといけない。
名辞「ソクラテス」の外延は、ソクラテスという人、一人を要素とする「集合」と考えるのである。
つまり、次が、名辞ソクラテスの外延なのである。

そして、この様に考えると、上の三段論法
の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ
の形、しかも、すべてがA型の全称肯定命題であることがわかる。
つまり、
の本当の意味は、
ということになる。
不自然なようにも感じるが、
という命題も、恐竜が絶滅寸前で、恐竜が最後の一ぴきしかいない状況では、「ソクラテスは人間である」と同じ様な状況となることを考えれば、必ずしも可笑しな理解ではない。
先ほどの三段論法の前提、つまり、1-3の内の、1と2
の状況を、今までのようなベン図で重ねて図示してみると
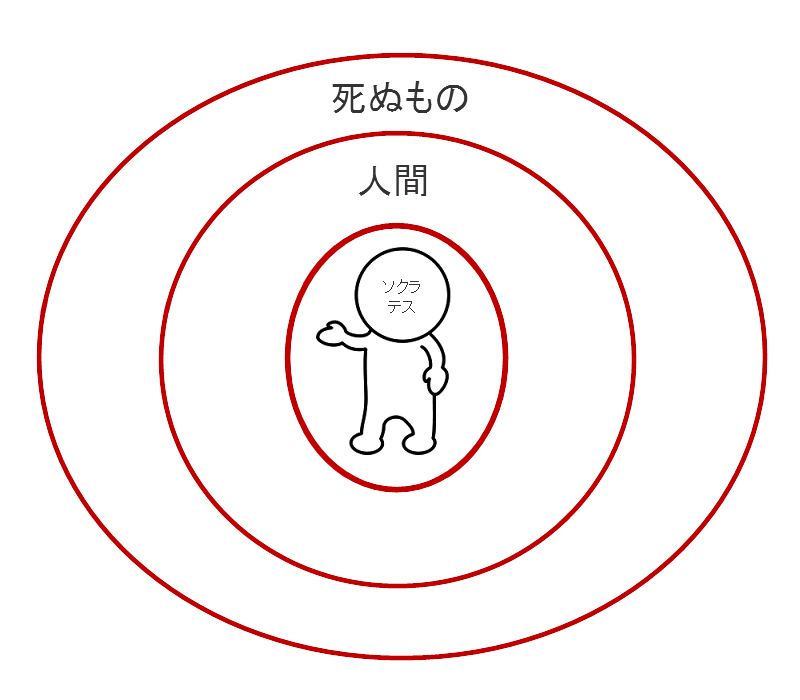
となる。あきらかに、
が分かる。つまり、有名な「ソクラテスは死ぬ」という三段論法は、数学でいう
つまり、
のことである。
これは
がどちらも全称肯定命題として理解されたとき、 A be B B be C の、中間の B をとって作った A be C という全称肯命題は、二つの前提が正しいときには正しいことを意味している。
同様のことを、1,2 と A be C のそれぞれを、全称肯定、全称否定、特称肯定、特称否定のすべてのパターンで考えて、その推論が正しいかどうかを、ひとつひとつ検討したもの。
それがアリストテレス論理学の主要部分であるシロギズムの理論(三段論法の理論)であった。
また、Keynes の教科書の59頁にもあるように、実は、「ソクラテスは人である」という命題は、「ソクラテスという人がいる」という特称肯定命題と考えることもできる。
この様な特称名辞を主語にする categorical proposition の奇妙さは論理学者の間で議論があったらしい。
多くの論理学書が書かれたが、Keynes の教科書が、その典型である様に、この「特称名辞」の問題は、常に喉に刺さった棘であったのである。
そして、次に説明する「数理論理学」で、初めて、この問題が解決される。
アリストテレス論理学の問題点として、上に挙げた特称名辞の問題と並んで、二つの問題があった。
それは、
という問題だった。
1番目の問題は、例えば、「AはBとCを両親とする子供である」のようなものを直接的に表すことができないという問題である。
このような時、アリストテレス論理学では、たとえば、「Aは両親Dの子供である」、「Bは両親Dである」、「Cは両親Dである」など、不自然な表現しかできないのである。
また、2番目の問題は、リンク先シロギズムの理論で見た様に、正しい推論のパターンは、一つ一つ吟味すればわかるものの、
それを説明する統一的な方法がないという問題であった。
そのため、シロギズムの理論のテーブルにある Barbara, Barbari の様に、これを覚えるための符丁さえ発明されていたのである。
そして、19世紀になると、これらの問題だけでなく、哲学、言語学、数学などの様々な動機の元に、論理学の見直しが始まり、
20世紀の初頭まで、その論理学の改革の運動が続いた。
その多くは、現在では忘れ去られているが、たとえば、ジョン・スチュアート・ミルやジョン・デューイなどの著名な学者たちが、
新論理学を提案したのである。
実は、禅などに結び付けて考えられがちな西田幾多郎の哲学も、そして、京都学派の哲学者たちの多く哲学理論も、
新論理学の創出を目指したものだと考えることもできるのである。
そして、第二次世界大戦後、特に1970年位から、そういう様々な「新論理学」の中で、ある一つの流れが、
外を圧倒して強くなり、現在、例えば日本では、ほぼ完全に「論理学」の地位を占めるようになったものがある。
それがイギリスの数学者ジョージ・ブールに発する、数理論理学である。
このブールの数理論理学は、哲学の一分野であるアリストテレス論理学への代数学の応用だったが、
アメリカの万能学者チャールズ・サンダース・パースなどにより、大きな改良がくわえられ、上に書いた三つの問題がすべて解決された。
これがイタリアの数学者ペアノにより、数学の記述に応用されるようになる。
そして、その影響を受けた、イギリスの哲学者兼数学者バートランド・ラッセルによりペアノの論理学が拡張され、
20世紀の冒頭に、数学の近代的基礎の原型が完成する。
しかし、次回説明する、ラッセルのパラドックスが発見され、数理論理学は一度危機に陥る。
それを、ラッセルと、アルフレッド・ホワイトヘッドが、Principia Mathematica という危機回避策を作りだし、
これが、後期の特殊講義の主役となる、ヒルベルトとその弟子たちのヒルベルト学派に継承され、
数学の近代的基礎の創出に応用されたのである。
このブール→パース→ペアノ→ラッセル→ヒルベルト学派という系譜が、第4、あるいは、第3のルートである、論理学ルートなのである。
前期では、この内、ラッセルが、彼のパラドックスを発見するまでを解説する。
まずは、この系譜の源、ブールの話から始める。
イギリスの数学者ジョージ・ブールは、代数学の一分野、不変式論の創始、演算子法という微分方程式の解法の発明(解析学)などでも知られる数学者のブールは、
アリストテレス論理学の「categorical proposition は二つの名辞の関係しか扱えない」、「シロギズムの理論に一貫した統一性がない」という欠点を解消すべく、
名辞を代数式の変数 x, y, ... で表し、これの演算、たとえば、積 xy などを考え、数式のようなものをで名辞のようなものを表し(ブールの式には、名辞として解釈でないものが入っていたので、式がすべて名辞なのではない)、それを等号で結び等式を作り、代数と同じく、幾つのかの規則を決めて、その等式を変形することにより、シロギズムの理論を置き換えた。
たとえば、彼の1854年の著書 The Laws of Thought では、x を「白いもの」white things, yを「羊」という名辞だとすると、xy は「白い羊」を表す、と説明して、
xy=yx
が成り立つ、と説明している。
ブールは、categorical proposition を表すために、v という記号を導入し、たとえば、All Y's are X's を y=vx と表現したが、これは現代的な立場からは、全く受け入れることができない方法であり、現在では使われていない。
しかし、ブールが、名辞を使い、categorical proposition を彼の論理学の式で表そうとしたように、これはアリストテレス論理学への数学的方法の応用である。
つまり、哲学の一分野に数学を応用したものであった。
また、ブールがアリストテレス論理学を否定したという説明がされることがあるようだが、これは間違いで、ブールはアリストテレス論理学を改良しようとしたといえる。
さらに現在、ブール代数と呼ばれるものがあるが(1,2)、これはブールの論理学とは大きく異なるものである。
最初の数理論理学といえるブールの論理学では、「ソクラテス」の様な特称名辞が、「人間」などの名辞と同じ名辞であるという所は、アリストテレス論理学と同じであった。
しかし、アメリカの万能学者パースは、ブールの論理学の、この部分を見直し、1870年代から1880年代にかけて、関係の論理学 logic of relatives というものを創出した。
これが現在の述語論理学というものの先駆けである。
注.実は、ほぼ同じようなものが、ドイツの数学者ゴットロープ・フレーゲにより、ほぼ同時期に出版されているのだが、数学者のフレーゲの仕事は、ラッセルの仕事を通して、それが知られるようになるまで、ほとんど知られることがなく、特に数学者に与えた影響は非常に小さい。そのため、これは、この講義では取り扱わない。一方で、パースの論理学は、数学者ペアノの論理学の元となり、やがて数学の近代的基礎で使われることとなった。パースは、様々な分野で仕事をしているが、プラグマティズムの創始者であることもあって一般的には哲学者として捉えられることが多い。そのパースの論理学が、数学の基礎となっていったのに比べ、数学者フレーゲが数学に影響をあたえることがほぼなかった一方で、分析哲学と呼ばれている英米系の哲学には、今でも大きな影響を与えていることは、面白いことである。
パースの論理学には、三つのポイントがあった。それは
である。
この最初のものが、特称名辞の特殊な取り扱いを論理学から放逐することとなった。
アリストテレス論理学では、
A loves B
のような二つのもの関係を記述するとき、
A is a lover of B
の様に書く。
また、
A benefits B
は同様に categorical proposition
A is a benefactor of B
に翻訳する。
しかし、パースは、このような二つのもの関係を記述するとき、
i loves j
i benefits j
を、数学の記号を使って、それぞれ
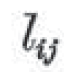
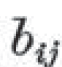
と書く方法を導入した。
パースは、これらを関係 relation と考え、自分の論理学を logic of relatives と呼んだが、
現代では、これらを
L(i,j)
B(i,j)
と書き、述語と呼んでいる。
アリストテレス論理学では、
A be B
が基本で、これは集合論の記号を使えば、
A⊆B
だったのだが、
パースでは、
L(i,j)
が基本で、これを集合論の記号を使えば
(i,j) ∈L
のように考えるのである。
ただし、 (i,j) は、i と j の対(数学では順序対という)である。
この様な述語の記号(述語記号)を導入したパースは、
さらに、quanifier 量化子と呼ばれる記号Π、∑を導入して、
「全ての者は、誰かを愛しており、また、その者に施しをなす」
あるいは
「全ての者は、誰かを愛しており、また、その者に恩をなす」
を、
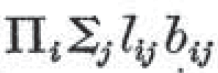
と書いた。
パースが行った述語の導入は、数学の関数
f(i,j)
や数列
aijのような記法にならったものである。
量化子は、さらに数学の記法を論理学に応用したものである。
これを説明しよう。
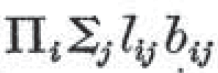
の
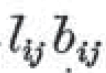
の部分は、 lij と bij の掛け算を意味している。
ブールでは、掛け算は、二つの名辞の共通部分を表していたが、
パースには、もう名辞の概念がなく、述語になっている。
パースでは、
L(i,j)
は
(i,j) ∈L
のように proposition、つまり、命題と理解されるので、
それは categorical proposition と同様に、真になるか偽になる。
そこで、1を真、0を偽と考えると、
1×1=1
1×0=0
0×1=0
0×0=0
となるが、これは
真かつ真 は 真
真かつ偽 は 偽
偽かつ真 は 偽
偽かつ偽 は 偽
という「かつ」の真偽の規則と一致する。
+の方は
1+1=2
1+0=1
0+1=1
0+0=0
となるが、2は1以上なので、1とみなすと、
1+1=1
1+0=1
0+1=1
0+0=0
となり、これは
真または真 は 真
真または偽 は 真
偽または真 は 真
偽または偽 は 偽
という、数学でつかわれる「または」と一致する。
さらに、マイナスを否定とみなして、
-0=1
-1=0
と定義すると、
真の否定 は 偽
偽の否定 は 真
で、これも代数が真偽と否定の規則を、そのまま表現することになる。
この考えをさらに発展させたものが量化子である。
たとえば、
All persons love Tom.
を考える。
数学の変数(あるいは添え字) i が人間、つまり、persons を表すとする。すると、この文章は、
All i love Tom.
になる。さらにパースの述語記号を使い、Tom を j と書くと、これは、
All i lij
と書ける。
ところが、もし、人(persons)にすべて通し番号がついているとすると、 i や j は、0, 1, 2, 3…という数字だと思ってもよい。
もし、Tom の番号が5番だとすると、これは、
All i li5
と書ける。
ところが、これは
l05 かつ l15 かつ l25 かつ l35 かつ l45 かつ l55 かつ l65 …
つまり、
l05 × l15 × l25 × l35 × l45 × l55 × l65 …
つまり、
l05 l15 l25 l35 l45 l55 l65 …
のことである。
数学では、こういう数列の積を
Πi li5
と書く。これがパースのΠの意味であり、それは、「すべての i に対して、li5 である」を意味している。
同じように、以上の説明の「かつ」、つまり、ブール代数の掛け算を、ブール代数の足し算、つまり、「または」に置き換えると、
l05 または l15 または l25 または l35 または l45 または l55 または l65 …
つまり、ブール代数の記法では、
l05 + l15 + l25 + l35 + l45 + l55 + l65 …
となるが、これは数学の記号を使うと、
∑i li5
になる。これがパースの∑の意味で、それは、「ある i に対して、li5 である」を意味している。 つまり、「誰かが Tom を愛している」「ある人が存在して、その人は Tom を愛している」となる。
以上の説明から、
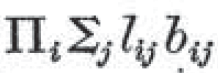
を直接的に日本語に訳してみると、
すべての人 i に対して、ある人 j が存在して、i は j を愛していて、かつ、i は j に施しをする
と読める。つまり、
全ての者は、誰かを愛しており、また、その者に恩をなす
と読める。
ただし、この「愛」はキリスト教における愛で、パースは、
これらの例文をトマス・アキナスの神学大全からとっている。
そのことからもわかるように、パースの目的は、ブールの場合と同様に、
アリストテレス論理学の改善であり、数学を応用しているが、
数学の基礎付けに、これを使おうとはしていない。
パースにとり彼の論理学は、彼の記号学の一部分だったといわれている。
最初、数理論理学は、言わば、数学の哲学への応用だったのである。
しかし、これが次のペアノで大きく変わる。