2017.06.27,28に文章を改善、および、Lindemann のKronecker への言及の情報を追加
2017.07.02: リンデマンがリンデンマンになっていたので訂正。
カントル(1845-1918)はベルリン大学の出身で、ワイエルシュトラス、クンマー、クロネッカーなどに数学を学んだ。女子校などの数学教師を経て、1869年に最初の大学での職である、ハレ大学の私講師となる。後に正教授となり、ベルリン大学の教授となることを熱望しながらも、そのキャリアの最後まで、この大学の教授として過ごした。少年期から精神的に不安定なところがあり、後には精神病の発病を繰り返した。
カントルは最初、クンマーやクロネッカーと同じ、数論(整数論)の研究を行ったが、ハレ大学に移ってから、先に在籍していた、同じワイエルシュトラス門下のハイネの影響を受けて、解析学、特に三角級数 trigonometric series(フーリエ級数)の収束についての研究を行った。そして、これがカントルの集合論に繋がったと言われている。(e.g. 1、2)
この三角級数の収束の研究は、ワイエルシュトラスのイプシロン・デルタ論法で収束を定義する方法が大きな貢献をしている。ハイネやカントルが研究した「関数の級数の収束」に関連したことを、コーシーが研究しているのだが、アーベルという数学者に間違いを指摘されている(参照)。
これは、コーシーが、現在、各点収束 pointwise convergence と呼ばれているものと、一様収束 uniform convergence と呼ばれているものを区別できなかったからだと信じられている。
この二つの収束の差を、ワイエルシュトラスのイプシロン・デルタ論法で書くと、次の様になる:
まず、実数 x 上の実数値関数 f(x) と、関数の列{fn(x)}nを考える。
関数列{fn(x)}nが、f(x)に各点収束するとは
「任意の 実数 aに対して、任意の正の実数εに対して、…」という部分が日本語として変だが、これは「任意の 実数 aに対して、次の括弧の中のことが成り立つ(任意の正の実数εに対して、…)」という意味である。
より自然な日本語だと「任意の 実数 aと正の実数εに対して、ある自然数 m が存在して、任意の自然数 n に対して、n>m ならば |f(a)-fn(a)|<ε となる。 」となるのだが、一様収束の文と比較するために、わざと変な日本語のままにしてある。
関数列{fn(x)}nが、f(x)に一様収束するとは
各点収束と一様収束の二つの定義を比べると、前者の青字の部分が、後者の赤字の部分に移動しただけだとわかる。
数式の形などは変わっておらず、文章の構造だけが変わっている。つまり、数学というより、論理が変わっている。
これが、コーシーの様な優れた数学者でも勘違いをしてしまった理由だろうと思われる。
一様収束と各点収束の違いを最初に指摘したのは、ワイエルシュトラスの先生だったChristoph Gudermannだが、彼はそれを正確に定義することはできず(せず?)、これを正確に定義したのはワイエルシュトラスが最初とされている。これを参照。
こういうのを明確にできるのが、イプシロン・デルタ論法の優れたところだが、同時に、これは数学に論理学的なものを持ち込むものでもあった。
ワイエルシュトラスのイプシロン・デルタ論法は、この様に解析学における概念形成や証明方法の厳密性を飛躍的に高めた。
それが、どの点でも連続だが、どの点でも微分不可能なワイエルシュトラス関数のようなものについて、精密に議論することを可能にした。
その意味でイプシロン・デルタ論法は解析学の革命だったともいえる。
そして、そういう方法を使い、カントルは三角級数を研究し、次の「カントールの一意性定理」と呼ばれているものを証明した。
カントールの一意性定理
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、すべての実数xで有限の値に収束するとしよう。その時、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
これが一意性定理とよばれるのは、もし、すべてのxで同じ値になる二つの級数があったら、この定理から、両者の係数an, bnが一致することがわかるからである。(係数an- bnの第三の級数を考え、それにこの定理を使う。)
カントルは、これをベルリン流の厳密な方法で証明し、さらにそれを拡張していった。
どの様に拡張したかというと、
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、すべての実数xで有限の値に収束するとしよう。その時、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
の赤字の部分に例外の点を入れて、それを段々と増やしていったのである。
最初の拡張は、「すべての実数xで有限の値に収束するとしよう」の代わりに、
有限個の例外を除き、それら以外のすべての実数xで有限の値に収束するとしよう。その時、その有限個の例外点を除き、すべてのxに対して、
だった。
これは、集合の言葉を使うと、次のように言い換えることができる、
実数の有限集合E があって、
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、Eに属さない、すべての実数xで有限の値に収束するとしよう。その時、Eに属さない、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
Eは例外の点の集合なのだから、この定理を拡張するには、Eを大きくすればよい。
実際、カントルは、この集合Eをどんどん大きくしていったのである。
しかし、集合Eには要素が有限という条件しかないのだから、これを拡張するには、無限個の要素をもつ集合を考えるしかない。
カントルがやったことは、このEをドンドン大きく、また、複雑なものにしていくことだった。
そういう風な、実数直線の部分集合Eの複雑なものを研究する分野を、点集合論という。
点集合、つまり、実数の集合には、区間[0,1]のようなものだけでなく、幾何学的にみたとき非常に不思議なものが沢山ある。
たとえば、このカントルの三角級数研究の時代に発明されたものではないが、カントルの名前がついた、カントル集合というものなどは、その典型で、それを使って作るカントル関数というものは「悪魔の階段」と呼ばれているほどである(参考1,2)。ちなみに、カントル集合は、フラクタルと呼ばれるものの典型例である。
カントルが彼の一意性定理を証明したのは1870年のことだが、例外集合Eを拡張するに従い、カントルは実数を正確に定義して、その性質を厳密に論じる必要性を感じ、1872年のある論文で、有理数の数列の内、コーシー列と呼ばれるものを使って実数を定義した。
5月29日の講義で述べたように、この1872年は、デーデキントが、彼の切断概念を発表した年である。
これが切っ掛けとなり、1872年にはすでに二人の交流が始まっている。まず、互いの論文を送りあい、そして、夏には、Gersau というスイスの保養地で、共に夏の休暇を過ごしている。この時、デーデキントは41歳、カントルは27歳だった。
二人は、夏の休暇の後も、二人は手紙で数学について議論を続け、この交流が、いわゆるカントル集合論を生み出す。
この説明は、この講義で示している新歴史観以前の通説そのものである。つまり、この良く研究された歴史は、新歴史観でも保持されている。
そして、この講義では、それを「解析学ルート」と呼んでいるわけである。
またまたの繰り返しとなるが、新歴史観は、少なくともこの講義での新歴史観は「カントルは集合論の祖ではない」というのではなくて、「カントルひとりだけに集合論の始まりを見るのはおかしい」という立場であることに注意。伝統的な集合論史、つまり、解析学ルートの歴史の定評のあるものとしては、Joseph Warren Dauben の、Georg Cantor : His Mathematics and Philosophy of the Infiniteがある。
ただ、この講義の下敷きになっている、Laugwitz と Ferreiros の歴史観では、Cantor に対しての態度がかなり違う。Laugwitz はかなり冷たい態度をとっていて、これから紹介するカントルの「純粋集合論」は、彼の著書ではほとんど無視されているが、Ferreiros は、解析学ルートを丁寧に紹介しており、「純粋集合論」の歴史も詳しく紹介している。しかし、 Ferreiros の著書のテーマが集合論の歴史である一方、 Laugwitz の著書は、Riemannの伝記だったのだから、これは当然ともいえる。
さて、話を戻して、カントルの集合論の発展について説明しよう。
カントルの点集合論は、最初、三角級数の収束の一意性定理のような、伝統的な解析学に属するものだった。
それはワイエルシュトラスの新理論によって武装されていたので、それ以前の数学者、たとえば、コーシーのような人でも、できなかったような精密な議論で構築されていた。
つまり、ベルリン流の「ワイエルシュトラスの厳密性 „Weierstraßsche Strenge“」のゆえに可能になった解析学の理論だった。
ちなみに、この「ワイエルシュトラスの厳密性」という言葉は、それ以前とは、レベルの違う厳密性を要求したワイエルシュトラス流の数学における厳密性を指していう言葉である。
カントルは、その厳密性を身に着けており、それにより、彼の三角級数研究を実行したのである。
つまり、それは、ベルリンの伝統の上に乗った、正統のベルリン流数学だったのである。
たとえば、Ferreiros は、彼の書籍の158ページで、カントルが1870年に一意性定理の証明に成功したとき、Schwartz という数学者が、カントルに手紙を送り、それが自分たちの属するベルリン学派の数学の厳密性が成し遂げた素晴らしい業績であると賞賛し、その中で、自分たちは、数学ロマンチスト、数学詩人 den mathematischen "Romantikern" und "Poeten" とは違うのだと誇らしげに書いていることを指摘している。そして、Ferreiros は、この数学ロマンチスト、数学詩人は、リーマンのことを言っているのだろうとしている。実は、リーマンも、三角級数の研究をしていて、リーマンが考えたF(x)関数というテクニックを、カントルは、その一意性定理の研究に使っているので、根拠はないものの、ありそうなことである。
しかし、カントルが例外集合Eを無限の方向にドンドン拡大し続けるに従い、このベルリン学派からの賞賛は、だんだんと非難に変わっていった。
ワイエルシュトラスの厳密性で武装したカントルは、それを使い、無限集合の世界では、直観に反するような不思議な現状が起きることを発見していき、もともとの数学より、その無限の不思議さの方に興味を示すようになり、Ferreiros が言う「思惟の迷宮」 Labyrinth of Thought に突き進んでいったからである。
ベルリン学派の多くの数学者には、それは、数式とその計算に基づく、厳密なベルリン数学からの逸脱と捉えられたのである。
カントルが論文として出版したものでは、逸脱は、例外集合Eの不思議な性質に自身に注目する様な研究として表れている。
しかし、実は、すでに、早くも1873年11月29日のカントルからデーデキントへの手紙で、カントルは、後に彼の集合論の要となる一対一対応による無限集合の濃度の問題について書いている。(Dauben p.49)
この手紙で、自然数の集合と実数の集合の間に一対一対応があるかどうか、という問題を提起し、おそらくはないだろうが、どうしてかわからないという意味のことを書いているのである。
この問題がわかったところで、別に彼が当時行っていた三角級数の研究には、役立たない。
しかし、カントルは、そういうものに興味を持ち、ひたすら、その方向に突き進んでしまったのである。
先に、構造主義の数学という話をして(たとえばこれ)、20世紀の数学は、構造主義が主流だったと説明した。
そして、構造とはたとえば、リーマンの計量とか、リーマン面、多様体で使われる位相とか、デーデキントの代数の体や環などのように、、まっさらの集合の上に、盛られたものだと説明した。
計量や位相、そして体や環、これらが幾何の構造であり、代数の構造である。集合は、そういう絵を描くためのキャンバスのようなものだった。
しかし、そういう構造というものがない、まっさらな集合、キャンバスだけで、面白い数学理論ができるだろうか?
常識的に考えれば無理なのだが、カントルは、上の1873年のデーデキントへの手紙にあった、一対一対応を考えると、何も構造がない純粋な集合でも、無限集合の世界では、点集合論のカントル集合の様な、不思議な世界が開けてくることを発見したのである。
それが、彼の超限基数、超限順序数の理論だった。
無限集合は、有限集合にない不思議な性質を持つ。
そのいくつかは、古くから知られており、例えば、有名な所では、ガリレオ・ガリレイの「新科学対話」にある所謂「ガリレオのパラドックス」という次の様なものがある。(現代の言葉を使って書いてある。ガリレオが「集合」などと書いているのではない。)
正整数を2乗してできる数を、平方数という。つまり、1, 4, 9, 16, 25,..... である。しかし、2, 3, 5, 7, 8,.... などは平方数ではないので、平方数の全体は、正整数の全体の、それより本当に小さい一部分である。
それにも関わらず、総ての正整数1, 2, 3, 4, 5, ..の集合と、総ての平方数1, 4, 9, 16, 25,..... の集合は、12=1, 22=4, 32=9,.... のように一対一に対応する。
25までの25個の数からなる集合{1,2,..., 25}に限定すると、その平方数の集合{1, 4, 9, 16, 25}は、{1,2,..., 25}の、それより本当に小さい一部分、いわゆる真部分集合である。
25までの平方数の集合{1, 4, 9, 16, 25}は5個しか要素がないので、要素が25個ある集合{1,2,..., 25}との間に一対一対応はない。
この様に、有限集合ならば、その真部分集合との間に一対一対応がないことは明らかである。
しかし、無限集合では、その真部分集合で、元の無限集合と一対一対応がつくものが必ず存在するのである。
最初、解析学への応用のために複雑な無限集合を考えていたカントルだが、段々と、この様な有限集合と大きく異なる無限集合の不思議な性質そのものに興味を惹かれるようなり、純粋集合論とでもよぶべき、「集合論のための集合論」を探究していった。もちろん、それはベルリン流の堅実な数学からすると、まったくの異端だった。
最初の重要な発見は、1873年11月29日のデーデキントへの手紙で提起した、自然数の集合と実数の集合の間に一対一対応があるかという問題の解決で、1873年12月7日のことであった。
自然数と一対一対応する集合を可算集合というので、これは実数の全体の集合は非可算集合だということである。
自然数の集合は実数の集合の部分集合だから、これは実数は自然数より、ずっと沢山あるという結果でもあった。
そして、この事実の簡単な応用として、「超越数が存在する」という有名な定理の非常に短い別証明を導くことができた。
超越数というのは、実数で、6月5日の資料で説明した代数的数でないもののことを言う。
代数的数が可算であることは比較的簡単に示せるので、実数が非可算であれば、当然、超越数が存在することになるのである。
超越数が存在することは、19世紀半ばに初めて証明されたが、カントルの証明は、それより遥かに簡単だった。
この当時、超越数の研究のテーマは、特定の数、例えば円周率πが超越数であることを示すことに移っていたので、カントルの示した結果は、数学的には重要なものとは言えなかった。
それでも、これは数学の伝統的問題への貢献があったので、例えばワイエルシュトラスは、これを評価して出版を勧めている。
しかし、円周率πが超越数であることを証明したリンデマンに、「あなたの円周率についての美しい研究は何の役にたつのか?無理数というものが存在しないのに、どうしてそういうことのを考えるのか?」と言ったとされるクロネッカーは、当然、カントルの仕事を高く評価するようなことはなかったと思われる。
注.この逸話は、リンデマン自身が記録したものだが、クロネッカーの研究で知られる米国の数学史家、エドワーズは、クロネッカーがその通りに行ったはずはないとしている。実際、クロネッカーは円周率を彼の研究や講義で使っているし、それが超越数であることも講義中に述べていることをエドワーズは指摘している。また、無理数√2などは、代数的数なので、クロネッカーやクンマーの数学では自然な存在なので、そのことからも、クロネッカーが、この様に言ったとしたら変である。しかし、クロネッカーが、デーデキントやカントルのような「実数の定義」のようなものを無意味だと思っていたことは確かの様であり、リンデマンの様な研究の方向性を、あまり意味がないものとして考えていた可能性はある。(詳しくは、H.M.Edwards, Essays in Constructive Mathematics, Essay 5.5 を参照)
そのためか、カントルは、自らが属するベルリン学派の数学者ではなく、ゲッチンゲン学派の数学者デーデキントに自分の発見を書簡で報告しながら、集合の理論を開拓していった。
その中で、カントル自身にとって、エポックメイキングだったと言われているのが、平面の点と直線の点の間に一対一対応があることの発見だったと言われる。これは1877年のことであり、出版されたのは翌年である。
カントルは、この様なことはないと信じていたので、自身の発見に驚き、デーデキントに自らの発見について意見を求める手紙を書いた際に、フランス語で「私は見るが、信じない」と書いたことは有名である。
実数直線は、二次元平面の中の、ほんの一部なので、カントルの驚きはもっともといえる。
ただし、カントルは驚いたが、これは分かってみれば簡単に証明できる。細かい点で工夫が必要だが、簡単に言えば、0.123456.... という無限小数は、奇数桁だけとると、0.135.... 、偶数桁だけとると0.246.... という二つの数に「分解」できる。それぞれを、x, y とすると、これは、平面の点の座標 (x,y) だと見なせる。この対応により、実数と実数の対の集合の間に1対1対応をつくれるのである。
このな風な、一見パズルの様な工夫を使いながら、カントルは彼の集合の理論を構築していった。それは、それまでの数学とあまりに違うものだったので、多くの数学者が、胡散臭いものと考えたのは無理もなかったであろう。
集合論が数学の基礎として定着した現在でも、これに違和感を唱える数学者は後を絶たない。確かに、それは数学の伝統からは、あまりに乖離したものだったのである。
注. そして、逆に、それが集合論やカントルが数学の一般向け書籍で持てはやされる理由にもなっている。そのため、集合論や、これから説明する記号論理学、そして、それらによる数学の基礎に対する態度が、幾何、代数、解析のような伝統的分野の数学者とそうでない人たちの間で、大変に違う原因となっている。数学の主流は、現在でも、幾何、代数、解析にルーツを持つ諸分野であるが、哲学者などは、この事実を見落としがちで、数学に対する間違ったイメージを持つ人が大半で、それが哲学者と数学者の意思疎通を妨げている。
1877年に「私は見るが、信じない」と書き送ったころのカントルは、n次元平面を「n 次元連続多様体」 eine stetige Mannigfaltigkeit von n Dimensionen と呼んでおり、リーマンの影響が用語に見て取れる。
また、このころのカントルは、リーマンの幾何学に興味をもっており、自分の集合論の研究と、それを結び付けて考えていたことが、デーデキントとの間の書簡の分析で分かっている。(Ferreiros Chap. VI, 4.3)
このリーマンの数学への注目がシンボライズするように、カントルは、平面と直線の一対一対応など、新規な発見を続けることにより、段々とベルリン数学の正統から逸脱していった。
それに従いベルリンの数学者たちは、カントルの数学を異端視するようになり、たとえば、当時、非常に評価が高かったクレレ・ジャーナルと呼ばれる専門誌の編集をおこなっていたクロネッカーは、カントルの集合論関係の論文を、この雑誌から排除するようになっていった。
このカントルとクロネッカーの対立は、アメリカの数学者兼小説家のE.T.ベルがベストセラーの数学読み物「数学をつくった人びと」で、二人の対立を面白おかしく取り上げたことで、良く知られているが、実は、このベルのストーリーは大半が嘘である。カントルとクロネッカーの話だけでなく、「数学をつくった人びと」の他の数学者たちのストーリーも、殆どベルの創作と言えたので、数学史家や数学者からの厳しい批判を浴びている。
このクロネッカーとカントルの対立がどんなものだったのかは、今ではかなり詳細にわかっている。この対立は哲学的なもの、あるいは、数学はどうあるべきかという数学論的なものであった。しかし、これに並行して、デーデキントとクロネッカー・クンマーの「対立」が起きており、これは数学論的なものもあったが、数学上の対立の要素の方が大きかった。
この二つの対立は、後期の2も含めて、この講義の重要なポイントとなるのだが、海の日の休みを計算に入れていなかったために時間が不足気味なので、これは後期の講義で扱うこととする。
さて、話を戻して、この様なベルリン学派からの逸脱による孤立の状況を支えたのは、デーデキントの存在が大きかったと思われる。
ここまで説明して来た様に、カントルは、自分でも「見るが信じられない」純粋集合論の緒結果を、常にデーデキントに書簡で知らせ、あまりに当時の数学の手法から逸脱していたために、彼自身にも不安が残った、それらの結果の証明の「正しさ」についてデーデキントの意見を聞いている。これがカントルの集合論の開拓の大きな支えになったのは言うまでもないだろう。
しかし、このデーデキントとの関係も、やがて終わりを迎える。
実は、カントル集合論の最初の成果と言えた、超越数の存在の別証明の発見の際、代数的数が可算であることを最初に発見したのはデーデキントだったと思われるのである。少なくとも、二人の書簡中に、それが現れるのは、デーデキントからカントルへの書簡の一つなのである。しかし、カントルは、それを論文にする時、デーデキントが、それを発見したことを書かなかった。
デーデキントは、大変に控え目で争いをさける人だったことが知られているが、それもあってデーデキントが、このことでカントルを問い詰めることはなかったが、後にカントルが、「理由はわからないが、どもデーデキントは自分に対して怒りの感情をもっているようだ」と、ある手紙に書いているように、実際にはデーデキントはカントルに対して複雑な感情を持っていたようである。
実はカントルは、幼少のころから精神的に不安定だったといわれ、1884年には、精神病を発症し、以後、死去するまで、発病と回復を繰り返した。この時期は、1884年5月の最初の発病以前であるが、行動に普通ではない所があったとしても不思議ではない。その「異常性」が、カントルの集合論という、それまでの数学から逸脱したものの開拓に寄与したという人もいるが、その高く空中を飛翔するかのような思考と性格は、常識人中の常識人で堅実そのものだったデーデキントと、反りが合わなくなるのは必然だったのかもしれない。
この両者の関係の悪化が顕在化するのは、1881年にハイネの死去により、空席になったハレ大学の教授職にカントルがデーデキントを招請しようとしたのに対し、デーデキントがこれを断った頃からだともいわれる。Ferreirosは、これをクロネッカーとの対立などでベルリン学派から孤立したカントルが、デーデキントに支えを求めたのだろうとしている。しかし、デーデキントは、それを断ったのである。(Ferreiros VI, 5)
デーデキントは、現在は、工科大学となっているブラウンシュヴァイクの工業学校の教師として一生を過ごした。現在は、世界有数の大学である、チューリッヒ工科大学で解析学を教えた時、切断の概念を発見したことは、すでに述べたが、この時は、チューリッヒ工科大学は、まだ、新設の工業学校であり大学ではなかった。19世紀には、工学は大学で教えるような学問と見なされていなかったからである。
つまり、デーデキントは、一度も大学の教師だったことは無かったのである。偉大な数学者としては、珍しいことである。学者というものは、カントルが特にそうであったように、評価の高い大学や研究機関に在職するためには、例えば日本では単身赴任をしたりして家庭を犠牲にするのことの方が多い。
しかし、デーデキントは、そういうカントルや多くの学者とは、全く違った人物だった。彼が在職した工業学校は、彼の生地にあり、また、彼の父が運営していた学校でもある。彼は一生独身を通したが、妹などの新族がブラウンシュヴァイクにいた。また、給与も悪くなかったようだし、学校のいわゆる雑事も積極的にこなしたようである。それらのことから、デーデキントは、充実した人生に満足していたようで、大学に職を求める気はなかったようなのである。
これは、ベルリン大学の教授職を渇望するなど、常に評価に飢え、精神的に苦しんだカントルと大きな対照をなす。この二人ほど対照的な人物たちが、集合論の草創期に重要な役割をしたことは非常に面白い事実である。
そして、それは二人の集合論への関わり方にも現れていた。その話は、この講義でいう現代の数学の基礎への4ルート(幾何・代数を統合して考えれば3ルート)の最後の一つである論理学ルートの際に説明する。そして、今は、その論理学ルートの立役者である哲学者バートランド・ラッセルの論理学による数学の基礎づけ研究につながり、この後の数学の基礎の歴史に大きな影響を与えることになった、カントルの超限数の理論について説明しよう。
カントルの集合論研究を支えた、デーデキントとの書簡のやり取りは1882年にカントールが書き送った書簡をデーデキントが無視して返事を送らなかったときに終わった。そして、その書簡で導入されていたのが、この超限数の理論だったのである。(Ferreiros, p.201)
「論理学ルート」の解説で説明するように、デーデキントの集合論は、数学を厳密に基礎づけるということに力点があった。そのため、彼は実数、理想数に続いて、自然数を基礎づけるということまでしているが、カントルの態度は、まったく逆だった。
カントルは、ベルリン学派の中に留まっていたころは、三角級数の研究のための必要性から、実数を厳密に定義すると言う様なことをしていたが、ベルリン学派から逸脱し、集合論の翼を得て高く飛翔するようになるに従い、以前紹介した、Schwartz の言い方を借りれば、数学ロマンチスト、数学詩人の「想像の産物」を次々と考え出した。
その最大のもので、現代も純粋集合論の最も重要な概念であるものが、超限数の理論である。
先に、一対一対応により、有限集合の「要素の多さ」を比較できることを、運動会の玉入れの譬えを使って説明した。これは口頭で説明しただけで、資料には書いてないので、ここで記録すると次のようになる:
運動会の玉入れで、白組が勝ったか、紅組が勝ったかを判定するために、ひとつ、ふたつ、…と数えながら、篭から玉をひとつずつとりあげて外に放り出す。そうして、紅組の玉が早く尽きれば赤の玉の方がすくないのだから、紅組の負け、白組の玉が先に尽きれば白組の負けである。そして、もし、同時に篭の中の玉が尽きれば、両者の玉の数は同じなのだから、引き分けとなる。この引き分けの場合が、赤い玉の集合と白い玉の集合に一対一対応がついた場合である。
この一対一対応をとるには、「ひとつ、ふたつ、…」と数を使って数える必要はない。だから、数の概念がなくても集合の「要素の数」を「同数」かどうか判定できる。そのために、数えることができない無限集合、たとえば、自然数の集合や、実数の集合、平面の点の集合の「要素の数の比較」ができたのだった。
しかし、カントルは、1882年、この考え方を反転させて、無限集合の個数を表す超限基数というものを導入した。そして、それに関連して超限り順序数というものも導入した。つまり、無限の数を考えたのである。
これの理論的構成の詳細の説明は省くが、その理論の大雑把な構造を説明しよう。
そして、カントルは、これらの無限の数にたいして、和や積などを定義し、その性質を研究した。
平面は直線の点の対、つまり、座標(x,y)の集まりと見なせるが、この様な対(座標)の集合を直積集合といい、有限集合の場合は、対の要素をとってくる集合の個数の積がだけ要素があることがわかる。
それでカントルは、この直積集合の個数も、もとの二つの集合の個数の積と定めた。
実数の集合の基数をℵと書くが、平面と直線の間に一対一対応があるという結果は、要するにℵ×ℵ=ℵという事実を表しているのである。
実は、有限の数の場合には、0と1以外ではなりたたない、a×a= a というこの等式は、無限の基数の場合には必ず成り立つのである。
カントルは、このような不思議な定理を、超限基数、超限順序数双方で、次々と発見し証明していった。
しかし、カントルは、二つの重要な定理を成り立つと予想しながら、どうしても証明できなかった。
それが、次の二つであった:
カントルは、この二つの定理を証明できなかったものの、殆ど独力で、無限の理論である、純粋集合論を開拓していった。
カントルが開拓した純粋集合論では、当然ながら、超限基数と超限順序数の様な新しい概念を導入されると同時に、数々の定理が証明された。
その中で、特に「カントルの定理」と呼ばれている有名な定理がある。
これから、どんな集合でも、それより数の多い要素をもつ集合があるということが分かるので、超限基数論の言葉でいえば、「最大の超限基数はない」という事実がわかる。
aが A の要素ならば、{a} という集合は Pow(A) の要素なので、Pow(A) の方が、Aより以上の要素をもつ。
しかし、同数であることはない。つまり、AとPow(A)の間には、一対一対応はない、というのがこの定理である。
それの証明は、非常に簡単だが、対角線論法という面白い議論を使うので有名である。
しかし、この対角線論法が、厄介な問題を引き起こしてしまったのである。
証明は簡単なので、紹介しておこう。
背理法で証明する。
AとPow(A)の間に一対一対応 f :A→ Pow(A) があるとする。
集合Rを
R={x∈A|x∉f(x)}
と定義する。これはPow(A)の要素である。
fは一対一対応なので、f(a)=R となる a をとれる。つまり、
a∈Aを
f(a)={x∈A|x∉f(x)}
となるものとする。
そのとき、
a∈f(a) ⇔ a∈{x∈A|x∉f(x)} ⇔ a∉f(a)
となるので、これは矛盾である。
よって、この様な一対一対応fは存在しない。
この定理を、論理学ルートの立役者、バートランド・ラッセルは、間違いだと考えた。
その理由は、超限基数全体の集合の基数は、最大の超限基数となるはずだと考えたからである。
この事実は、ラッセル以前にカントルが気が付いているが、カントルは、これは集合には、矛盾したものと矛盾しないものがあるということの証明だと考えた。
この二人が気が付いた事実を、今では「カントルのパラドックス」という。
この奇妙な事態を、ラッセルは、彼の記号論理学で解決しようとし、さらに厄介な世界に踏み込んでしまうことになった。
数学の新基礎となるべき集合論、そして、ギリシャ以来の論理学が破綻してしまったのである。
ラッセル・パラドックスの発見である。
この話をするために、次の論理学ルートについて説明する。
今までの話の登場人物は、すべて数学者であった。
リーマンが自信を自然哲学者と考える哲学的傾向が強い人であったと言われるものの、
また、そのリーマンやカントルの理論が、当時のベルリン学派の立場からは、数学から逸脱しているものであったものの、
そして、カントルが、その様な自分の理論を哲学、さらには神学と結び付けて考えるようになったものの、
総ては数学者が、数学的目的で考え出したものである。
たとえば、集合論を神学にさえ関係づけたカントルも、集合論研究の最初の動機は、如何にも数学者らしい、
知的好奇心からであったことは、以上に述べた歴史から明らかである。
しかし、ここからの話は大きく異なる。
登場人物の多くは、哲学者や哲学と数学の境界で仕事をした人、あるいは、哲学の一分野である論理学に数学を応用しようとした人たちである。
つまり、ここからの話は、哲学ルートと言っても良いのである。
その哲学ルートが、このルートの立役者である哲学者バートランド・ラッセルにより、
古代ギリシャ以来の論理学が、数学と統合され、数理論理学、記号論理学
というものが誕生することにより、むしろ数学の一部に吸収されることとなり、
数学の近代的基礎が誕生するのである。
この最後の課程は、後期の講義で話すことになるが、前期では、
ラッセルが、論理学による数学の基礎づけ、所謂、論理主義というものを生み出し、
それにより数学の基礎を堅固にしようとしたが、カントルの定理のために、
ラッセルのパラドックスと呼ばれるものを発見して、
むしろ、数学と論理学の基礎を同時に破壊してしまったという話まで進む。
古い歴史観ならば、ここで19世紀における 数理論理学、記号論理学の発展の話から
始めるところだが、この講義では、Ferreiros に従い、この背景にある、
アリストテレス論理学、いわゆる、伝統的論理学から始める。
19世紀には、というよりラッセウが状況を変えてしまう、20世紀の初めころまでは、
論理学とは、伝統的論理学、アリストテレス論理学のことであったのである。
名辞は、英語では term といい、だから、アリストテレス論理学は、英語では term logic という。
名辞は、非常に大雑把に言えば名詞、あるいは、名詞とそれが指し示すものを合わせたものと思っておけばよい。
たとえば、
などが名辞である。例が大げさだが、これは昨年度までやっていた論理学の歴史という講義で使っていた、明治の論理学書から引用しているからである。
1のような名辞は固有名詞に対応する。つまり、指し示すものが一つである。2の様なものは多くのものを指す。
その意味でかなり性格が違い、英語で言えば単数形と複数形の違いがあるのだが、これを名辞論理学では、同じ名辞として扱う。
1の方は、英語では singular term、2は universal term という。日本語には、現在定着した訳語がないようだが、昨年まで使っていた明治の教科書では、特称名辞、通称名辞と呼ばれている。
この様な名辞を組み合わせてできるのが、次の命題である。
命題というのは意味を持つ文章のことだと思っておけばよい。
アリストテレス論理学では、命題の基本単位は、二つの名辞から作られる
A be B
という形であると考える。ここで、A と B が名辞。
たとえば、次のものはみなそういう形をしている。
孟子 is 人
孟子 is 中国人
孟子 is 学者
中国人 are 人
学者 are 人
以上は皆正しいもの。
しかし、
中国人 are 孟子
人 are 学者
は間違いである。
この A be B のような形の基本形の命題は、categorical proposition と呼ばれている。(現在定着した日本語訳はないようである)
この様に名辞を結ぶ be を コピュラ、copula、 繋辞(けいじ)、連辞(れんじ)といい、
A be B のAを主語、Bを述語という。
ここまでで、すでに分かったと思うが、アリストテレス論理学は、英語やドイツ語、ラテン語などの言語の構造に根ざしている所があり、例えば、英語を使うと説明しやすいが、日本語に例えて説明すると不自然になる。
そこで、以下では、経済学者 John Maynard Keynes の父である John Neville Keynes の論理学の教科書を使って、英語に引き当ててアリストテレス論理学を説明していく。
これが Keynes の教科書、Studies and Exercises in Formal Logic の第2版の、該当部分。Internet Archive 版
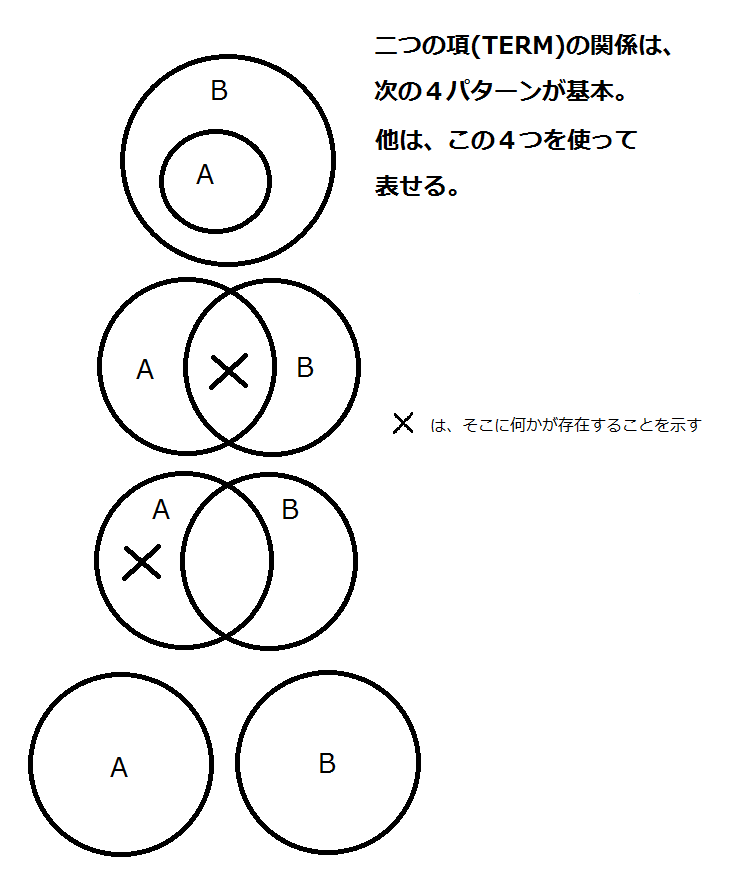
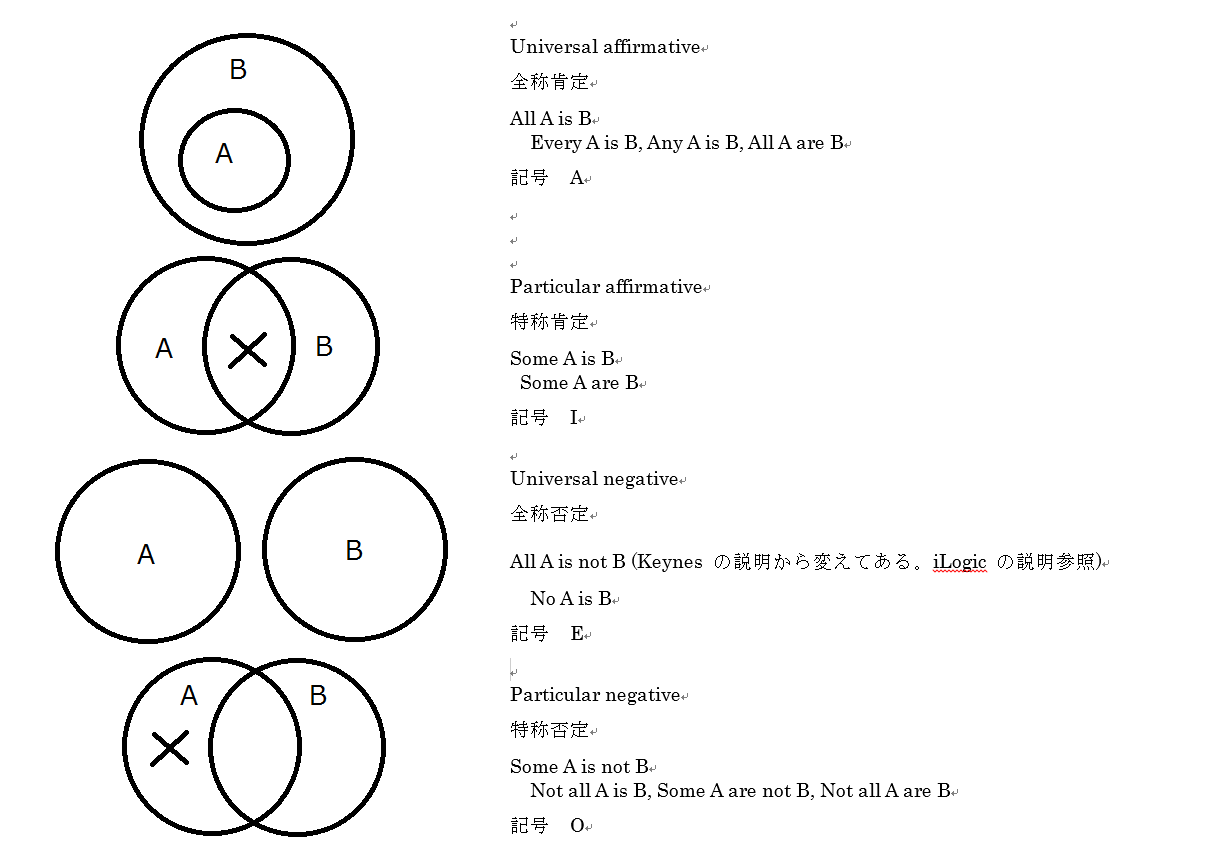
名辞を集合だと思うと、基本的には、二つの名辞の関係性には、対称的なものを同一視すると、次の4パターンしかないことがわかる。

他にもありそうな気が…
しかし、良く考えてみると、二つの名辞の関係は、本質的にはこの4パターンに還元できることがわかる。
たとえば、
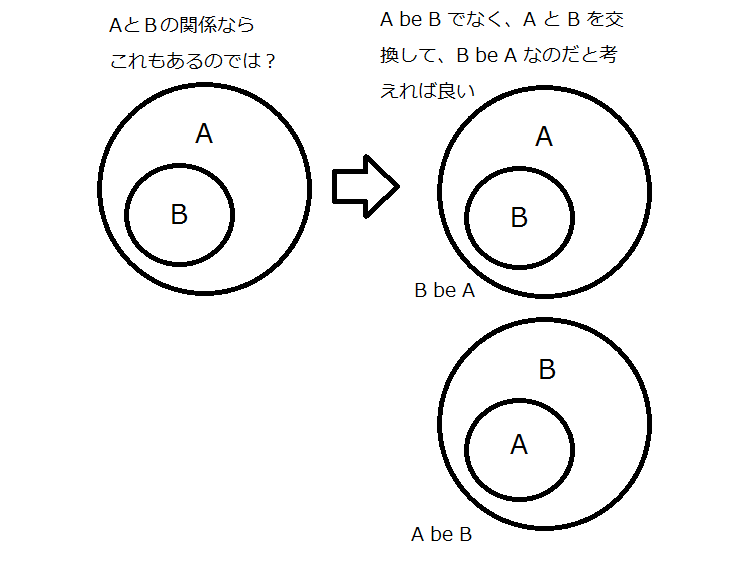
さらに…
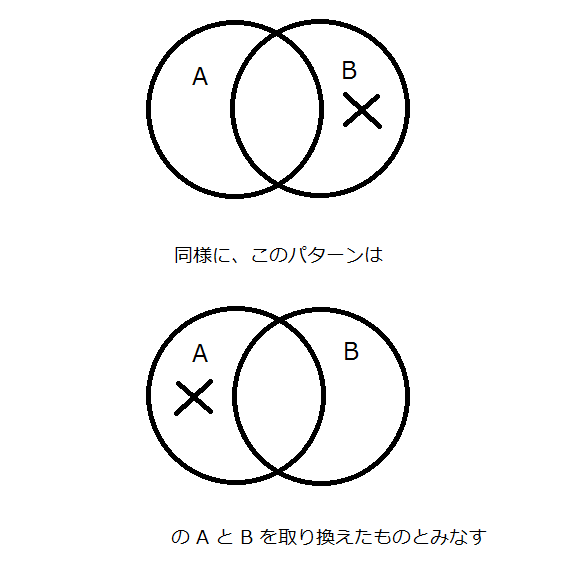
もうひとつ…
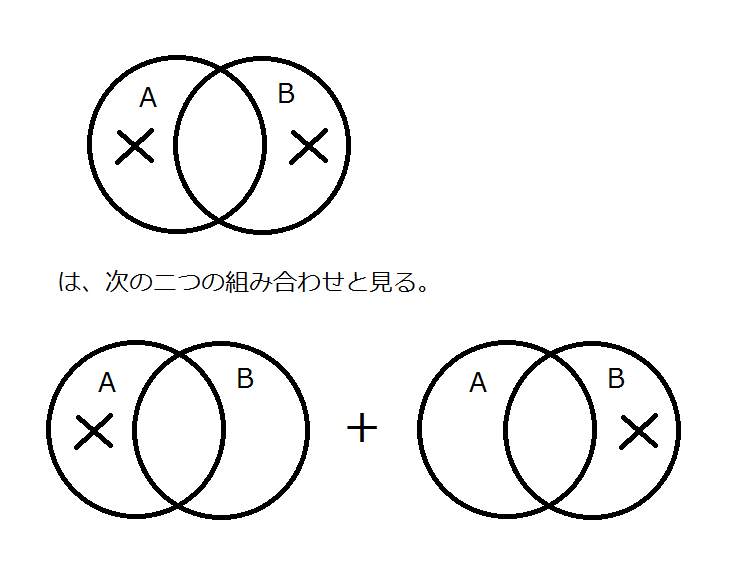
Keynes の教科書を参照すること
続く…