それをイプシロン・デルタ論法という。高校数学の美しい物語の説明。
最初の、
の A がゼロの場合に、f(x) が無限小の代わりになる。
そして、ワイエルシュトラスは、これを次のように定義したのである。

この定義には、中学生くらいまでに学ぶ数学しか使われておらず、それは実に合理的なものだったのである。
デーデキントの、これ以後の「数学の近代的基礎」への貢献の主な物としては、彼の畏友リーマンのリーマン面の理論を、ヘルマン・ワイル以後の位相空間を使う幾何学的理論ではなく、もし、リーマン面が存在するが、必然的に生じる「代数的」な存在で置き換えて説明する1880年の「一変数代数関数の理論」と、自然数の定義を試みた1888年のモノグラフ「数とは何か何であるべきか」の二つである。しかし、これらは、今までの話が1870年代前半までの話だったの対して、どちらも1880年代の話である。
そして、その1870年代には、デーデキントの数学と、ほぼ並行して、直接にはリーマン・デーデキントというゲッチンゲンの伝統とは関係ないベルリン大学出身の数学者による集合論研究が行われた。
それが、リーマン、そしてデーデキントの概念数学を、集合論の出発点とする歴史観が生まれるまで、集合論を一人で建築した天才として扱われていたベルリン大学出身の数学者ゲオルグ・カントルの数学であった。
最初の「体系だった集合論的数学」と言って良いデーデキントのイデアル論は代数に分類される。また、デーデキントの集合論的数学の思想的背景となったリーマンの概念数学におけるリーマン面や多様体の理論は幾何学に分類される。
これらに反して、カントルの集合論のルーツは、解析学であった。
つまり、集合論にいたる径、数学の近代的基礎への径には、ゲッチンゲンの幾何学・代数学ルートの他に、解析学ルートがあったのである。
この講義で紹介したリーマン、デーデキントを集合論のルーツとするような歴史観が生まれる前には、集合論のルーツは、この解析学ルートだと説明されることが多かった。例えば、林には、岩波文庫の「不完全性定理」の解説という「共著書」があるが(解説は200頁以上あるので実質著書(^^;))、Laugwitz の著書に影響を受けて書いた、この解説でも、従来の解析学ルーツから話を始めている。これら三つのルーツ、特にデーデキントとカントルのルートは、わずかにデーデキントが早かったが、ほぼ同時期に、しかも、互い影響を与えながら並行して進んだのであり、どれが本当のルーツかと問うのはあまり意味がなく、特に集合論という数学の一分野の歴史ではなく、数学の近代的基礎の歴史を考えるときには、これら三つのルートの総てを意識する必要がある。旧史観の問題点は、独立した一分野としての集合論の構築に最も功績があったカントルを重視し過ぎて、デーデキントなどの別ルートを軽く扱い過ぎた点にだけあると言ってもよい。
実は、これの他に、もう一つ、論理学ルートというものがある。
そして、論理学ルートは、この三ルートと、ほぼ並行に発展していたのである。
しかし、論理学ルートは、今までの話や、これから話すカントルの話と違い、少なくとも最初は、数学というより哲学の色彩が強かった。そのため、それがデーデキントの「数とは何か何であるべきか」や、カントルの集合論との関係を見出し、数学の近代的基礎に明瞭に影響を与え始めるのは、20世紀に入ってからのことである。そこで、これの説明は、カントルの集合論とデーデキントの「数とは何か何であるべきか」の説明の後に行うこととなる。
また、これらの異なるルートは、相互に影響を与え合っていることに注意して欲しい。特に、最初から数学に属する幾何学、代数学、解析学ルートは、その境界さえハッキリしないところがある。例えば、これから解析学ルートのルーツとして説明するワイエルシュトラスの解析学におけるε‐δ論法というものは、幾何学ルートの位相幾何学のルーツでもある。
注. シラバスでは、この講義(前期分)の内容は、次のようになっている:
第1回:「概説」
〇ゲーデルの不完全性定理とその背景としての集合論。
〇新史観と旧史観
第2~12回:「集合論の誕生」
〇揺らぐ数学の基礎:ラッセルの1903年の批判から
〇19世紀における新しい数学的存在の「量産」
〇リーマン面
〇コーシー、ワイエルシュトラスの解析学
〇クンマーの理想数
〇デーデキント・カントルの集合論
第13~15回:「数学の危機」
〇カントールたちのパラドックス
〇ラッセルの論理学と、そのパラドックス
〇ツェルメロのパラドックスとゲッチンゲン
今、やっているのが、赤字の「デーデキント・カントルの集合論」のカントルの集合論の部分。そして、これから解析学ルートのルーツとして説明を始めるのが、青字の「コーシー、ワイエルシュトラスの解析学」の話である。
論理学ルートにあたるのは、緑字の「ラッセルの論理学と、そのパラドックス」の項目であるが、これのルーツである、「数学というより哲学の色彩が強かった」と書いた研究、具体的に言えば、ブール、パース、フレーゲ、ペアノなどの数理論理学(記号論理学ともいう)の話は、時間的余裕があれば、この「ラッセルの論理学」の所で、余裕がなければ、後期の特殊講義「数学の近代的基礎の歴史(2)」で説明する。
ちなみに、下線をつけた「揺らぐ数学の基礎:ラッセルの1903年の批判から」は、導入のために使う予定だったものだが、導入の方法を変えたので、説明していない。実際の導入は、現代の数学の基礎が他の学問の基礎に比べて著しく「標準化」されているという事実の指摘から始めた。ラッセルの1903年の批判は、この現状に対して、20世紀初頭の数学では、その基礎の標準化ができておらず、もっとも厳密な学問と考えられることが多い数学でありながら、その基礎が揺らいでいるという批判だった。このラッセルの1903年の批判の話は、ラッセルの論理学や、後期の特殊講義で紹介する予定である。
すっかり標準化されて、実質的にはすべての数学者の間で、公式の基礎が共有されている現代の数学であるが、実はリーマンの数学をベルリン大学の数学者たちが疑問視していたように、19世紀においても、その基礎の標準化と数学者集団での意見の共有は成されていなかった。
つまり、19世紀の数学の基礎は揺らいでいたのである。そして、リーマンの数学は、その揺らいでいる数学の一つだったといえる。
しかし、リーマンの概念数学のような新しいスタイルの数学が揺らいでいたとしても、その時点の数学にとって大きな問題だったとは言えない。リーマンの数学の基礎の欠落より大きな問題は、解析学の基礎であった。解析学とは要するに、微分積分の理論のアドバンスドなものだと思えば良い。
つまり、ライプニッツとニュートンという数学、物理学、哲学の歴史上の巨人たちにより創始された学問であり、その始まりは17世紀中ごろのことである。
しかし、その後、約200年の間、解析学は大発展を遂げ、また、物理学へ応用されて、その大発展の重要な要因となりながら、その基礎は揺らぎ続けたのである。
現在の量子力学の基礎は、コペンハーゲン解釈というものが標準となっているが、これに違和感を持つ人は多く、最も有名な反論はアインシュタインからのものである。2017年6月11日京都新聞朝刊「天眼」に京大名誉教授の佐藤文隆は「量子力学90年とハイテク」というエッセイを寄せて、「彼(アインシュタイン)の問い質したポイントは、実は、今も解消したわけではない」と書き、今、この問題をハイテクを使って見治すと面白いのではないかと書いている。
しかし、佐藤が書いているように、この解釈に基づく電子技術は、コンピュータを生み出し、世界中で使われている。だから、理屈を言わずに使え、Shut up and calculate! という標語ができて、量子力学を学ぶ人の学び方の指針になっていたという。
19世紀の解析学は、まさに、そういう状況であり、基礎を詮索すると襤褸が出るが、それを気にせずに使うと、多くの成果が得られる、そういう状況だったのである。
そして、この「揺らぐ基礎」の最大の原因は、解析学に置いて中心的役割をする無限、たとえば、無限級数や無限小の概念にあった。これらの基礎を数学者はまともに説明できなかったのである。
また、これと同じく厄介だったのが、無限小という概念、あるいは、「数学的存在」だった。
19世紀になってコーシーとワイエルシュトラスにより、解析学の合理的な基礎が建設されるまで、数学者は、微積分学の創始者の一人、ライプニッツを含めて、dx などと書かれる無限小という、ゼロではないが、無限に小さいという数学的存在を考え、それを使って微分をしていた。そして、dx が無限小だったら、1/dx は、どのような数より大きい無限大だった。
そして、これがバークレイ僧正などの哲学者から批判を浴びていたのだが、数学者は、役に立つ Shut up and calculate という以外に有効な反論の術をもたなかったのである。
こういう混乱した解析学(微積分学)の状況を最初に改善したのが、 ナポレオン時代直後の1821年, パリの技術者養成校エコール・ポリテクニーク(理工科学校)での解析学教育のために、リーマンの話ででてきたコーシーにより書かれた教科書「解析学教程」だった。
コーシーは、無限大、無限小を考えるのを止めて、「高校数学応援ブログ web 問題集」の様に、無限大や無限小は、収束する有限のものの列だと考えた。たとえば、1,1/2, 1/4, 1/8, 1/16, …のように半減していく数列は0に収束する。無限小というのは、こういうものだと考えた。こう考えると、これの収束する極限を
dx と書けば、実は、1/dx は、 1, 2, 4, 8, 16,…となるから、それは無限に大きくなる「無限大」だと合理的に説明ができる。
コーシーの理論により、無限小、無限大という、神秘的とさえいえるものを数学から大幅に追放することができた。これによりバークレイ僧正の批判などに反論できるようになったと言って良い。
しかし、そのコーシーの方法でさえ、答えることができない問題が存在した。たとえば、コーシーの時代には、連続な関数は、この例の場合のx=0の時の様に、例外を除くと、微分可能であると広く信じられていたが、それが正しいかどうか、コーシーの方法で判定することは難しかった。
それを可能にしたのがワイエルシュトラスの方法だった。
ドイツの数学者ワイエルシュトラスは、コーシーが無限小を、ドンドン小さくなる(ゼロに収束する)列、あるいは、変量(変化する量)と考えたのに対し、「ドンドン小さくなる」という性質を、数と論理だけを使って定義した。
それをイプシロン・デルタ論法という。高校数学の美しい物語の説明。
最初の、
![]()
の A がゼロの場合に、f(x) が無限小の代わりになる。
そして、ワイエルシュトラスは、これを次のように定義したのである。

この定義には、中学生くらいまでに学ぶ数学しか使われておらず、それは実に合理的なものだったのである。
先に、数と論理だけを使って、と書いたが、この文章の日本語の部分が「論理の部分」、つまり、次の部分
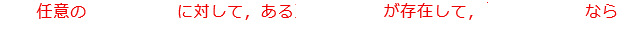
そして、残りが「数の部分」、つまり、次の部分

「論理の部分」は、「任意の(すべての)**に対して」、「ある**が存在して」、「なら(ならば)」の様な、フレーズが使われていて、これはすべて「論理学」で使われる表現になっている。
一方で、「数の部分」は、「正の実数」とか不等式の様に、高校までの数学で勉強した実数の概念や数式なのである。
「論理の部分」、つまり、論理学の部分は、人間が数学だけでなく、日常に推論する時につかうものである。
その論理学の推論として有名なものが、次の三段論法がある:
ソクラテスは人である。
すべての人は死ぬ者である。
よって、
ソクラテスは死ぬ者である。
これは古代ギリシャの哲学者アリストテレスが創始した「伝統論理学」とか「アリストテレス論理学」における、三段論法、シロギズムと呼ばれる、推論の理論の有名な例である。
ワイエルシュトラスの方法では、この論理の部分は、日常的な推論に頼っていた。
そして、アリストテレス論理学は、その我々の日常的推論を説明するための理論であったので、ワイエルシュトラスの方法とは、コーシーの解析学教程における「収束」の概念を、数の理論と伝統論理学に帰着させるものと言える。
この方法の威力は抜群で、たとえば、ワイエルシュトラスは、コーシーが解決できなかった、連続と微分可能性の問題を解くことができた。
そのために、彼が作った有名な関数が、ワイエルシュトラス関数である。
コーシーの時代には、連続な関数は、有限個の例外点を除いて、殆どの点で微分可能になると信じられていたことは既に述べた。
しかし、ワイエルシュトラス関数は、連続だが、あらゆる点で微分できない関数だったのである。
こういうものを作り出して、また、それが連続であるとか、どの点でも微分できない、と証明するには、ワイエルシュトラスの方法がないとできなかったのである。
ワイエルシュトラスの方法において、漸く、解析学、あるいは、微積分学の「揺らぐ基礎」が、数の理論と、論理学という、確固たる基礎に置き換えられたのである。
しかし、実際には、歴史は、ここで終わらなかった。
この確固たる基礎である筈の、数の理論と、論理学のさらなる探求が、無限小以上に厄介な問題を生むことになったのである。
しかし、その話をする前に、このコーシー、ワイエルシュトラスの理論から、どの様にゲオルグ・カントルが、彼の集合論に至ったか、その彼の集合論は、どの様なものだっか、また、その時にデーデキントが、どの様な役割を果たしたかを説明する。
カントル(1845-1918)はベルリン大学の出身で、ワイエルシュトラス、クンマー、クロネッカーなどに数学を学んだ。女子校などの数学教師を経て、1869年に最初の大学での職である、ハレ大学の私講師となる。後に正教授となり、ベルリン大学の教授となることを熱望しながらも、そのキャリアの最後まで、この大学の教授として過ごした。少年期から精神的に不安定なところがあり、後には精神病の発病を繰り返した。
カントルは最初、クンマーやクロネッカーと同じ、数論(整数論)の研究を行ったが、ハレ大学に移ってから、先に在籍していた、同じワイエルシュトラス門下のハイネの影響を受けて、解析学、特に三角級数 trigonometric series(フーリエ級数)の収束についての研究を行った。そして、これがカントルの集合論に繋がったと言われている。(e.g. 1、2)
この三角級数の収束の研究は、ワイエルシュトラスのイプシロン・デルタ論法で収束を定義する方法が大きな貢献をしている。ハイネやカントルが研究した「関数の級数の収束」に関連したことを、コーシーが研究しているのだが、アーベルという数学者に間違いを指摘されている(参照)。
これは、コーシーが、現在、各点収束 pointwise convergence と呼ばれているものと、一様収束 uniform convergence と呼ばれているものを区別できなかったからだと信じられている。
この二つの収束の差を、ワイエルシュトラスのイプシロン・デルタ論法で書くと、次の様になる:
まず、実数 x 上の実数値関数 f(x) と、関数の列{fn(x)}nを考える。
関数列{fn(x)}nが、f(x)に各点収束するとは
「任意の 実数 aに対して、任意の正の実数εに対して、…」という部分が日本語として変だが、これは「任意の 実数 aに対して、次の括弧の中のことが成り立つ(任意の正の実数εに対して、…)」という意味である。
より自然な日本語だと「任意の 実数 aと正の実数εに対して、ある自然数 m が存在して、任意の自然数 n に対して、n>m ならば |f(a)-fn(a)|<ε となる。 」となるのだが、一様収束の文と比較するために、わざと変な日本語のままにしてある。
関数列{fn(x)}nが、f(x)に一様収束するとは
各点収束と一様収束の二つの定義を比べると、前者の青字の部分が、後者の赤字の部分に移動しただけだとわかる。
数式の形などは変わっておらず、文章の構造だけが変わっている。つまり、数学というより、論理が変わっている。
これが、コーシーの様な優れた数学者でも勘違いをしてしまった理由だろうと思われる。
一様収束と各点収束の違いを最初に指摘したのは、ワイエルシュトラスの先生だったChristoph Gudermannだが、彼はそれを正確に定義することはできず(せず?)、これを正確に定義したのはワイエルシュトラスが最初とされている。これを参照。
こういうのを明確にできるのが、イプシロン・デルタ論法の優れたところだが、同時に、これは数学に論理学的なものを持ち込むものでもあった。
ワイエルシュトラスのイプシロン・デルタ論法は、この様に解析学における概念形成や証明方法の厳密性を飛躍的に高めた。
それが、どの点でも連続だが、どの点でも微分不可能なワイエルシュトラス関数のようなものについて、精密に議論することを可能にした。
その意味でイプシロン・デルタ論法は解析学の革命だったともいえる。
そして、そういう方法を使い、カントルは三角級数を研究し、次の「カントールの一意性定理」と呼ばれているものを証明した。
カントールの一意性定理
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、すべての実数xで有限の値に収束するとしよう。その時、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
これが一意性定理とよばれるのは、もし、すべてのxで同じ値になる二つの級数があったら、この定理から、両者の係数an, bnが一致することがわかるからである。(係数an- bnの第三の級数を考え、それにこの定理を使う。)
カントルは、これをベルリン流の厳密な方法で証明し、さらにそれを拡張していった。
どの様に拡張したかというと、
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、すべての実数xで有限の値に収束するとしよう。その時、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
の赤字の部分に例外の点を入れて、それを段々と増やしていったのである。
最初の拡張は、「すべての実数xで有限の値に収束するとしよう」の代わりに、
有限個の例外を除き、それら以外のすべての実数xで有限の値に収束するとしよう。その時、その有限個の例外点を除き、すべてのxに対して、
だった。
これは、集合の言葉を使うと、次のように言い換えることができる、
実数の有限集合E があって、
三角級数
1/2 a0+Σ(ansin nx+ bn cos nx)
が、Eに属さない、すべての実数xで有限の値に収束するとしよう。その時、Eに属さない、すべてのxに対して、
1/2 a0+Σ(ansin nx+ bn cos nx)=0
となるならば、an, bnは、すべてゼロになる
Eは例外の点の集合なのだから、この定理を拡張するには、Eを大きくすればよい。
実際、カントルは、この集合Eをどんどん大きくしていったのである。
しかし、集合Eには要素が有限という条件しかないのだから、これを拡張するには、無限個の要素をもつ集合を考えるしかない。
カントルがやったことは、このEをドンドン大きく、また、複雑なものにしていくことだった。
そういう風な、実数直線の部分集合Eの複雑なものを研究する分野を、点集合論という。
点集合、つまり、実数の集合には、区間[0,1]のようなものだけでなく、幾何学的にみたとき非常に不思議なものが沢山ある。
たとえば、このカントルの三角級数研究の時代に発明されたものではないが、カントルの名前がついた、カントル集合というものなどは、その典型で、それを使って作るカントル関数というものは「悪魔の階段」と呼ばれているほどである(参考1,2)。ちなみに、カントル集合は、フラクタルと呼ばれるものの典型例である。
カントルが彼の一意性定理を証明したのは1870年のことだが、例外集合Eを拡張するに従い、カントルは実数を正確に定義して、その性質を厳密に論じる必要性を感じ、1872年のある論文で、有理数の数列の内、コーシー列と呼ばれるものを使って実数を定義した。
5月29日の講義で述べたように、この1872年は、デーデキントが、彼の切断概念を発表した年である。
これが切っ掛けとなり、1872年にはすでに二人の交流が始まっている。まず、互いの論文を送りあい、そして、夏には、Gersau というスイスの保養地で、共に夏の休暇を過ごしている。この時、デーデキントは41歳、カントルは27歳だった。
二人は、夏の休暇の後も、二人は手紙で数学について議論を続け、この交流が、いわゆるカントル集合論を生み出す。
この説明は、この講義で示している新歴史観以前の通説そのものである。つまり、この良く研究された歴史は、新歴史観でも保持されている。
そして、この講義では、それを「解析学ルート」と呼んでいるわけである。
またまたの繰り返しとなるが、新歴史観は、少なくともこの講義での新歴史観は「カントルは集合論の祖ではない」というのではなくて、「カントルひとりだけに集合論の始まりを見るのはおかしい」という立場であることに注意。伝統的な集合論史、つまり、解析学ルートの歴史の定評のあるものとしては、Joseph Warren Dauben の、Georg Cantor : His Mathematics and Philosophy of the Infiniteがある。
ただ、この講義の下敷きになっている、Laugwitz と Ferreiros の歴史観では、Cantor に対しての態度がかなり違う。Laugwitz はかなり冷たい態度をとっていて、これから紹介するカントルの「純粋集合論」は、彼の著書ではほとんど無視されているが、Ferreiros は、解析学ルートを丁寧に紹介しており、「純粋集合論」の歴史も詳しく紹介している。しかし、 Ferreiros の著書のテーマが集合論の歴史である一方、 Laugwitz の著書は、Riemannの伝記だったのだから、これは当然ともいえる。
さて、話を戻して、カントルの集合論の発展について説明しよう。
カントルの点集合論は、最初、三角級数の収束の一意性定理のような、伝統的な解析学に属するものだった。
それはワイエルシュトラスの新理論によって武装されていたので、それ以前の数学者、たとえば、コーシーのような人でも、できなかったような精密な議論で構築されていた。
つまり、ベルリン流の「ワイエルシュトラスの厳密性 „Weierstraßsche Strenge“」のゆえに可能になった解析学の理論だった。
ちなみに、この「ワイエルシュトラスの厳密性」という言葉は、それ以前とは、レベルの違う厳密性を要求したワイエルシュトラス流の数学における厳密性を指していう言葉である。
カントルは、その厳密性を身に着けており、それにより、彼の三角級数研究を実行したのである。
つまり、それは、ベルリンの伝統の上に乗った、正統のベルリン流数学だったのである。
たとえば、Ferreiros は、彼の書籍の158ページで、カントルが1870年に一意性定理の証明に成功したとき、Schwartz という数学者が、カントルに手紙を送り、それが自分たちの属するベルリン学派の数学の厳密性が成し遂げた素晴らしい業績であると賞賛し、その中で、自分たちは、数学ロマンチスト、数学詩人 den mathematischen "Romantikern" und "Poeten" とは違うのだと誇らしげに書いていることを指摘している。そして、Ferreiros は、この数学ロマンチスト、数学詩人は、リーマンのことを言っているのだろうとしている。実は、リーマンも、三角級数の研究をしていて、リーマンが考えたF(x)関数というテクニックを、カントルは、その一意性定理の研究に使っているので、根拠はないものの、ありそうなことである。
しかし、カントルが例外集合Eを無限の方向にドンドン拡大し続けるに従い、このベルリン学派からの賞賛は、だんだんと非難に変わっていった。
ワイエルシュトラスの厳密性で武装したカントルは、それを使い、無限集合の世界では、直観に反するような不思議な現状が起きることを発見していき、もともとの数学より、その無限の不思議さの方に興味を示すようになり、Ferreiros が言う「思惟の迷宮」 Labyrinth of Thought に突き進んでいったからである。
ベルリン学派の多くの数学者には、それは、数式とその計算に基づく、厳密なベルリン数学からの逸脱と捉えられたのである。
カントルが論文として出版したものでは、逸脱は、例外集合Eの不思議な性質に自身に注目する様な研究として表れている。
しかし、実は、すでに、早くも1873年11月29日のカントルからデーデキントへの手紙で、カントルは、後に彼の集合論の要となる一対一対応による無限集合の濃度の問題について書いている。(Dauben p.49)
この手紙で、自然数の集合と実数の集合の間に一対一対応があるかどうか、という問題を提起し、おそらくはないだろうが、どうしてかわからないという意味のことを書いているのである。
この問題がわかったところで、別に彼が当時行っていた三角級数の研究には、役立たない。
しかし、カントルは、そういうものに興味を持ち、ひたすら、その方向に突き進んでしまったのである。
先に、構造主義の数学という話をして(たとえばこれ)、20世紀の数学は、構造主義が主流だったと説明した。
そして、構造とはたとえば、リーマンの計量とか、リーマン面、多様体で使われる位相とか、デーデキントの代数の体や環などのように、、まっさらの集合の上に、盛られたものだと説明した。
計量や位相、そして体や環、これらが幾何の構造であり、代数の構造である。集合は、そういう絵を描くためのキャンバスのようなものだった。
しかし、そういう構造というものがない、まっさらな集合、キャンバスだけで、面白い数学理論ができるだろうか?
常識的に考えれば無理なのだが、カントルは、上の1873年のデーデキントへの手紙にあった、一対一対応を考えると、何も構造がない純粋な集合でも、無限集合の世界では、点集合論のカントル集合の様な、不思議な世界が開けてくることを発見したのである。
それが、彼の超限基数、超限順序数の理論だった。
続く…