Zは整数の全体を表している。つまり、Rとは、a, b が整数である、a+b√-5 という形式の複素数なのである。これが和、差、積について閉じている、つまり、Rの二つの要素の和、差、積は、再びRの要素になること容易にわかる。しかし、除、つまり、割り算について閉じていない。
2017.06.07: 裸の王様の動画を入れかえ。他に文字化けしていたリンクを修正
19世紀は、多くの数学の新概念が登場した世紀だった。西洋の数学生まれた古代ギリシャでは、まだ複素数はなかった。それどころか、古代西洋にはゼロも負の数もなかった。
実はインドや中国の数学、つまり、アジアの数学では、かなり早い時期から、ゼロや負の数が、一人前の数として使われていたのだが、西洋では、その「存在」が忌避され、例えば、18世紀のイギリスには、負の数は存在しないと主張する影響力のある数学者がいた。少なくともイギリスの場合、負の数が十分な市民権を得たのは、19世紀のことである。(参照)
その19世紀になると、ゼロ、負の数、そして、正の数からなる整数、そして、実数、さらには複素平面の考え方がガウスらにより導入され、また、既に述べたコーシーやリーマンの複素関数の研究が行われるようになり、複素数も当たり前になった。(参照)それらが、数学の概念あるいは存在として認められたのである。
この19世紀の数学の「拡張」は、その程度では終わらなかった。たとえば、19世紀の中ごろに生まれたリーマン面が典型であるように、この世紀は、虚数 imaginary number の様な、imaginary、つまり、 想像上の存在と言える数学的存在が次々に「発明」された時代だった。
その様な新概念の一つに、すでに登場しているベルリン大学の数学教授、エルンスト・クンマーが導入した理想数がある。これは、ある意味で、20世紀数学の行方を決めたと言って良いほどの重要な概念なのだが、ベルリン大学の数式重視の伝統の故に、クンマーの理想数は、「非常に特殊な方法」で導入されており、そのために分かりにくいものであった。
それをデーデキントが、集合を使うイデアルという概念を導入して分かり易いものに作り替えた。実は、このデーデキントのイデアルの理論こそ、現代的な意味での集合論が、最初に展開され、かつ、出版された最初の例と考えることができるものなのである。
「概念で考える数学」は、リーマンの複素関数や幾何学についての研究の中で登場し、その中で抽象的な集合の概念が生まれたと考えられることは、既に述べた。この様な解釈を最初に提案した二人の歴史家、Laugwitz と Ferreirósは、彼らの著、Bernhard Riemann 1826-1866 と Labyrinth of Thought で、ともにリーマンとデーデキントの深い交友関係について述べている。
リーマンが現代的な集合の概念に到達していたと考え得る証拠は、「幾何学の基礎をなす仮説」に登場する「離散多様体」という言葉である。
リーマンは、この講演で、多様体 Mannigfaltigkeit という概念を導入し、それには連続の場合と離散の場合があるとしたのである。
そして、連続多様体が、すでに説明したリーマン面などをその例とする、「計量」の構造をもつ幾何学的な多様体のことであった。そして、それが20世紀における多くの数学の分野の大発展の基礎となったのである。
しかし、リーマンは、離散多様体については、それを構成するものを「要素」ということと、その量は、計量が後付けで追加される連続多様体の場合と異なり、数え上げにより内在的に定まっているとしただけで、ほとんど何も語らなかった。(連続多様体を構成するものは、リーマンは「点」と呼んだ。)
そのため、この謎めいたリーマンの離散多様体については、色々な解釈がされている。
たとえば、Ferreirósは、これを現代的な集合の概念のことだと解釈している。
その理由のひとつは、リーマンが、離散多様体の「量」は、数え上げ、つまり、要素の個数により決まる、と書いていることである。これは、後に説明する一対一対応をもとにしたカントールの離散集合論を想起させる。実際、カントールの集合論の基数の理論は、無限に拡張された個数の理論だからである。
そして、もう一つの証拠は、Ferreirós が指摘しているように、デーデキントがカントールに集合概念の名称として、リーマンが、その名称を使ったという理由で、Mannigfaltigkeit 多様体という用語を推していることである。
Laugwitz と Ferreirós の両者ともに論じているように、リーマンとデーデキントは親友であり、精神的に不安定であったリーマンをデーデキントが支えるという関係であった。また、リーマンの著作集を編集して出版し、未発表だった「幾何学の基礎をなす仮説について」を学界に紹介したのも、デーデキント(と、その盟友 H.Weber)であった。
つまり、あまりに直観的かつ大胆であり、また、出版もされなかったため、十分に理解されていたとはいいがたい、リーマンの思想と方法、特に、その思想を、最もよく理解できる位置にいた人物は、デーデキントなのであり、リーマンの新数学思想は、デーデキントの努力により広まったといえるのである。
そのデーデキントが、「幾何学の基礎をなす仮説について」で登場した「多様体」を、カントールに集合の名称としてすすめたということは、デーデキントが、リーマンの離散多様体を、カントールや彼の集合概念と同じ様なものと理解していたことを示唆する。もちろん、連続多様体も、現代的な定義に従えば、位相空間であり、それは点の集合なのである。
この様に、離散多様体が、現代的な集合と同じ様なものを意味していたと考える根拠はいくつかある。しかし、一方で、それが幾何学についての講演において言及されたものであり、リーマンの講演の対象が、n重に広がったもの、つまり、n次元空間であったことからすると、この離散多様体にも何らかの幾何学的イメージが付随していた可能性も捨てきれない。
リーマンの記述は、あまりに、曖昧で、それだけでFerreiróのような断定的結論を導くのは、些か、大胆過ぎる。そこで、本講義では、現代的な集合論のルーツを、リーマンとデーデキントという親友のペアに求めることにする。
つまり、リーマンの思想を直接聞くことができる立場にいたデーデキントが、リーマンの思想の中に、現代的な集合の概念を読み取った。そして、それがデーデキントにより広く学界に伝えられたと理解する。
果たして、リーマンがどこまで現代的な集合概念、つまり、個数という構造以外は、何の構造ももたない、数学のための真白なキャンバスとしての集合のイメージを持っていたかは史料的に判断するのは不可能として、その問題を問わないのである。
しかし、デーデキントというフィルターを通した後では、それは明白に現代的な集合概念となっているので、リーマン+デーデキントにより、現代的集合概念が誕生したとみなすのである。
物の集まりを数学の対象にしたのは、リーマンやデーデキントが最初ではないが、本講義では、それを数学の基礎に横たわるものとして、数学を行った人(たち)の最初が、リーマン+デーデキン、とくにデーデキントだとみなす。
そのデーデキントが、最初に集合を数学の対象として明瞭に用いたのは、彼のイデアル論でのことで1871年のことである。それは、ベルリン、ゲッチンゲンの双方で教鞭をとり、双方に大きな影響を与えたディリクレの講義ノートをデーデキントが編集して1871年に出版した際、その補足として公表された。
アメリカの哲学者 Avigad による、その解説つき英訳の中で、System とよばれているものが、デーデキントの集合である。その初出は、このPDF資料の12ページで、デーデキントが体 field, Körper を定義している所である。(この段階では、体の要素は整数などの具体的な数に限られている。)
この体は、数学を行う場所のようなもので、この段階では、まだ、数学の対象、つまり、図形や、数のような位置にはないが、同じ訳の38ページにいたると、イデアル ideal と呼ばれるものが、 System 、つまり、集合として定義される。それをそのまま引用すると次のようになる:
We ground the theory of the numbers of o, i.e. all the integers of the field Ω, on the following new concept.
1. A system a of infinitely many numbers contained in o will be called an ideal if it satisfies the following pair of conditions:
I. The sum and difference of any two numbers in a is again a number in a.
II. Each product of a number in a and a number in o is again a number in a.
(原文では、o, a はドイツ文字)
これが、以前示した「切断」の定義と同じ様なパターンになっている。つまり、集合を一つあることにし、それが満たすべき条件がリストされ、そのリストの条件をすべて満たすものを「切断」とかイデアルと呼んでいるのである。
切断(X1,X2) の定義
実はデーデキントが切断の概念を考えたのは、彼がチューリッヒの工業専門学校で教えていたころで、1850年代のことである。しかし、そのアイデアが公表されたのは、1872年のことであった。また、デーデキントのオリジナルな流儀では、現代的な「切断を実数とする」というような定義ではなくて、切断を使って、実数の連続性を公理化するものだったので、切断自体が数学の対象としての存在だったのではなく、実数のような対象の性質を表すためのツールだったと理解すべきである。
それに対して、この1871年のイデアルは、それ自身が、数の拡張であり、整数のような、数学の対象と同じステータスにあった。その故に、これこそが、デーデキントの「数学の基礎づけの道具としての集合の使用」の始まりとみなせるのである。
デーデキントは、これを皮切りに、次々と、集合を用いた、数学的存在を導入し、そして、それを用いて数学を書き換えていったのである。
先にベルリンとゲッチンゲンの数学の流儀の違いについて述べたが、実は、この最初の数学的集合論とでもいうべきデーデキントのイデアル論は、そういう抽象的概念を嫌い、数式に基づくことこそが数学の本流だとするベルリンの数学から生まれた。
イデアルは、クンマーが代数的整数というある種の複素数の拡張として、1847年に導入した理想数 Ideale Zahlen というもののデーデキント版だったのである。
クンマーの理論は、ベルリンの気風を反映して、イデアルのような抽象概念を嫌ったために、分かりにくい理論構成になっていた。それは、その実体を全く定義せず、しかも、それがあたかもあるかの様に語る理論であった。つまり、幽霊を語るかの様なものだったのである。
このクンマーの理想数の理論について、簡単に説明しよう。
a+bi の、a,b がともに整数となる複素数をガウス整数という。これは、リーマン、デーデキント、クンマーなどのすべての源流をなすともいえる大数学者ガウスによるものである。
複素数の全体は体をなすが、整数は割り算がいつもは割り切れないので、体にはならない。この整数の全体のように、体の公理から、割り算の可能性の公理を除いたものを、環 Ring (正確には可換環)という。
ガウス整数の全体も可換環となり、整数とおなじく、割り算の商と余りや、約数の概念を定義できる。そして、さらには、素数とか、素因数分解も定義できて、素因数分解の一意性も成り立つのである。参考1、参考2
クンマーは、このガウス整数とよく似た数の体系を研究したが、その数体系では、素因数分解の一意性が成り立たなかった。そこでクンマーは、理想数という概念を「導入」して、素因数分解の一意性を成り立たせようとしたのである。
しかし、その時、クンマーは理想数を「存在しないまま」にしたのである。
この奇妙な状況が、デーデキントに、集合で理想数にあたるイデアルを定義させることになったのである。
理想数の概念は、クンマーによる「算術の基本定理の一般化」の研究の中で生み出された。
正整数に対しては、素因数分解の一意性がなりたつ。つまり、任意の正整数は素因数分解可能であり、また、その分解の方法は一通りしかない。所謂、算術の基本定理である。
上に説明したように可換環と呼ばれる代数的構造の世界では、割り算や素数、素因数分解にあたるものを定義できる。そして、ガウス整数の環の場合には、整数の場合と同様に、素因数分解の一意性が成り立つ。普通の整数はガウス整数だから、これは算術の基本定理が、整数より広い数に拡張されたのだと言える。
ベルリン大学の数学者クンマーは、この様な「算術の基本定理の拡張」を研究し、例えば、次のような環Rの場合には、素因数分解はできるが、その一意性が成り立たない、つまり、2つ以上の素因数分解の仕方があることを発見した。
![]()
Zは整数の全体を表している。つまり、Rとは、a, b が整数である、a+b√-5 という形式の複素数なのである。これが和、差、積について閉じている、つまり、Rの二つの要素の和、差、積は、再びRの要素になること容易にわかる。しかし、除、つまり、割り算について閉じていない。
注. a=1, b=√5iの場合、a/b は、(-1/5)√5i となって、-1/5 が整数でない。
つまり、このRは可換環なのである。
この可換環Rでは、6は、次の二通りに因数分解できる。
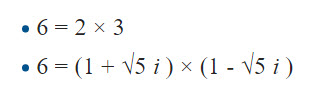
理由は省くが、2、3、1+√5i, 1-√5i は、全部、Rの「素数」つまり、これは1と-1以外では割り切れない。
つまり、素因数分解が二通りあることになり、算術の基本定理が成り立たないのである。
そこでクンマーは、「理想数」という仮想的な数を導入して、これらの4つ数がさらに「理想数」で割り算できて、その理想数の範囲の素因数分解はひとつしかないと考えたのである。
注.クンマーが、何故、この様なことを研究したか、その直接の動機はわかっていないらしい。ただ、この様な可換環で算術の基本定理が成り立つと、それを使って、当時まだ未解決だった有名なフェルマーの定理が、特別の次数の場合に証明できることが知られていて、クンマーも彼の理想数の理論を、フェルマーの定理を多くの場合に証明するためにつかっている。そのため、フェルマーの定理を証明するためだったと言われることが多いが、数学史家によっては、これに異論を唱える人もいる。フェルマーの定理は、有名なので、数学者の大きな研究のターゲットだったと誤解され勝ちだが、数学の理論の本流からは外れているという数学者も多く、クンマーの理論は、もっと数学の本流に位置するものだと考えている数学者が多いようだ。
つまり、「素数」である2、3、1+√5i, 1-√5i は、実は「素数」でなく、さらに次のように因数分解できると考えたのである。
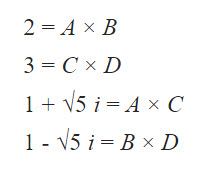
実際には、2、3、1+√5i, 1-√5i は、全部、Rの「素数」なので、こういうA,B,C,Dは存在しないのだが、これらを理想数と呼んで、あたかも、存在するかの様に考えたのである。
こういう場合、新しい数を導入して数の体系を拡張するものである。しかし、クンマーは、理想数という言葉は導入したものの、それを新しい数学的存在とは考えなかった。
新しい数学的存在を導入する代わりに、クンマーは、このA,B,C,Dのようなものが「あったとしたら」、その計算結果がどうなるかというようなことを、その当時の既存の数の範囲の中で完全に説明できる理論を作った。
なぜ、そういうことができたかというと、クンマーが扱った拡張された整数、例えば、Rの構成要素である、√5、i、Zなどが、そして、さらにはRの要素のすべてが代数的数と呼ばれるものだったからである。
代数的数とは、有理数を係数とする方程式の解となる数を言う。
有理数 r が代数的数であることは x-r=0 という方程式を考えればわかる。また、√5がそうであることは x2-5=0、i がそうであることは x2+1=0、という方程式を考えればわかる。そして、代数的数の和、差、積は、また代数的数になる(この解説の定理2)。つまり、Rの要素は全部代数的数である。
代数的数は方程式の解だが、ある代数的数 r を、その解とする様な方程式は無数にある。たとえば、p(r)=0 ならば、a*p(r)=0 も成り立つからこれは当然で、しかも、a として、任意の多項式 q(x) に, r を代入した q(r) でも良いのだから、q(x)*p(x)=0 という方程式を考えれば、与えられた代数的数を解とする幾らでも大きな次数の多項式があることさえわかる。
しかし、 r を特徴づけるのは、そういうものの中で「一番小さいもの」であり、それを最小多項式という。たとえば、√5の最小多項式は x2-5=0、i の最小多項式は x2+1=0 である。
r が代数的数なら、r の最小多項式は、一つしかなく、ある意味で、この方程式が r の「定義」、あるいは、その本質の記述、5月1日の講義資料で説明した、ポール・ロワイヤル論理学の用語で言えば内包なのである。
ある代数的数の最小多項式の係数がすべて整数であるとき、それは代数的整数と呼ばれる。たとえば、整数や、√5や i などは、すべて代数的整数であり、Rの数は、すべて代数的整数であるが、1/2 は、そうではない。代数的数の全体が体を成すように、代数的整数の全体は可換環となり、あたかも整数のような性質を持つ。
クンマーが扱った数は、実際には、Rではなくて、この代数的整数の一種で、円分整数と呼ばれるものだった(Rは、クンマーの理論を説明するめにデーデキントが考えた例であり、こういう解説では良く使われる)。円分整数は代数的数であるから、もちろん、その一つ一つには、それを「定義」する最小多項式があった。
そして、この当時、既に相当に進化していた代数方程式の解についての理論、特に共役というものについての理論を使い、与えられたひとつの円分整数の最小多項式を元に、その円分整数が何個の「理想数である素因子」を持つかを計算する方法をクンマーは与えることができたのである。
そして、そのそれぞれの理想数素因子を、数式により「名指しする方法」を与えることもできた。
そして、さらには、その名指された理想数素因子が、別に任意に与えられた円分整数を割り切るか否かの条件を、「理想数を使わない代数的数の範囲の数式の割り算の条件」で代用できたのである。(詳しくは、H.M.Edwards,The Genesis of Ideal Theory, Archive for History of Exact Sciences, Vol. 23, No. 4 (31.XII.1980)の pp.324-326 を参照)
つまり、クンマーは、代数的整数が理想数を因子として持つと仮想的に想定し、その理想数について直接語るのではなくて、理想数を素因子としてもつと仮定された代数的整数の定義、つまり、最小方程式について語ることにより、間接的に「理想数素因子」について論じたのである。
クンマーは、肝心のA,B,C,Dの「実体は何か」ということは、決して説明しなかった。つまり、クンマーは、ないもの(理想数)を、あたかも存在するかのように語ったのである。
これは、クンマーが、「理想数とは如何なる存在か」という問題を解決できなかったからというより、意識的に、存在という哲学的問題を避けた可能性が高く、こういう不思議な方法をとったのは、クンマーが数学をある種の自然科学のようにとらえたからだという説もある。(この本の Jacqueline Boniface の論文)
しかしながら、どういう哲学的動機があろうと、それが実に奇妙な方法であることには変わりはない。
その奇妙さは、童話の「裸の王様」を使って説明してみよう。
まず、このYouTube のアニメを見よう。
詐欺師や人々の言葉や手つきに注目:
また、シャーロックホームズは実在の人物だと信じ込むシャーロキアンの行動も、これに似ている。
クンマーの理想数は、まさにこんな感じで導入されたのである。
実は、この様な「存在しないものに対して、あたかも存在するかのように振る舞う」という行動は、現代の社会では当たり前になっている。
それは拡張現実と呼ばれるもので、たとえば、ポケモンGOが、そうである。
ポケモンGOというものを全く知らない人が、ポケモンGOのプレイヤーが歩きながらゲームに没頭している姿を見たら、非常に奇妙にみえるだろう。
それは存在しない理想数について語るクンマーや、王様の衣装が詐欺だと知っている人間が、王様たちの行動を見て感じる奇妙さと同じである。
しかし、スマホ上のポケモンを見ているユーザーにとって、それは、本当に存在するものなのである。
遠距離の二人のプレイヤーが行うチェスに、通信チェスとか、郵便チェスというものがある。
その対局の方法は、こんな風で、たとえば郵便チェスなら、「d2 のポーンを、d3 に」という風に書いて送るのである。
クンマーの数式だけに頼る理想数の方法は、この通信チェスの「d2 のポーンを、d3 に」という通信文に似ていた。
それは、例えば Goole map 上にピンを立てて場所を示すのでなくて、北緯、東経の数字で、場所を示すようなものである。
大変面倒であるし、直観的でない。
現在では、もちろん、ITの発達のお陰で、スマホやPCのアプリを使ったネット上のチェスの対極が可能であり、こういう「記号」「数値」による情報の交換が、目の前の仮想的チェス盤で、あたかも実物のチェス盤でプレーしているかの様に行えるようになっている。
そして、何もない目の前の道路にポケモンが現れる、ポケモンGOも、同じ仕組みを使うITの産物なのである。
ポケモンGOのモンスターは、何も、その実体がスマホやポケモンGOのデータセンターに棲んでいるわけではない。
モンスターの実体とは、実は、ポンスターの位置を示す緯度・経度のデータ、モンスターの向きを表す数値、モンスターの種類を表すID、モンスターの性質(つかまりにくさなど)を表すデータやアルゴリズム、そして、モンスターの画像をディスプレイに描くためのモンスターの3Dモデルなどからなっているのである。
こういうITを使えば、ポケモンが、現実に付け加えられた「存在」として、我々の視覚の中に実際に生まれ出でるのである。
実は、19世紀、20世紀の数学者たちは、集合を、このITの様に使い、理想数や、リーマン面に、ポケモンGOのモンスターの様な「形」を与えることにより、これらの天才的発明を、平均的数学者でも手の届くものにしていったのであり、それが「数学の近代的基礎」だったのである。
注.この講義では、説明できないが、実は、サイバー空間で、ポケモンGOの世界を作り出す方法は、数学者たちが集合を使って、仮想的数学存在を作り出した方法と非常に近い、また、歴史的にも関連があるものである。
そして、その嚆矢はクンマーの理想数理論を「可視化」した、デーデキントのイデアル論であった。
次に、これを説明しよう。
クンマーは、理想数を「王様の衣」のように扱った。その方法で重要なのは、たとえば、ある理想数が、他の数を割り切る、たとえば、仮に「現実に存在する数」である、Rの数に限定すれば、上の例のA,B, C,Dが、現実の代数的整数 a+b√5i を割り切る条件を具体的に語ることができることであった。
つまり、「Aは x を割り切る」という理想数Aとx の関係が成り立つ条件を、x に対して決めることができればよい。ただし、xはa+b√5iという形で、a,b が整数であるような代数的整数、つまり、上に定義したRの要素である。
それならば、その「関係」を利用して、Aとは、{x∈R|Aは x を割り切る}という集合のことだと思えば良い。
何故かと言えば、y∈{x∈R| Aは x を割り切る} ⇔ Aは y を割り切る (y∈R) となるのだから。
と、考えた人がいた。それが、すでに何度も登場している、リヒャールト・デーデキントだった。
デーデキントの切断の所で、既存の有理数のみを使って、√2という、新たな無理数を作り出す時、x<√2 と √2<y という関係を考えて、x の集合と、y の集合の対として、√2を作った。
これは、順序という関係により、√2が、他の数と持つ関係を記述して、それにより、√2というものを記述しようという方法である。
理想数の理論では、「割り切れる」という関係が何より大切だったので、切断と同じ戦略をとるとすれば、αが理想数だとして、{x∈R| αは x を割り切る}という集合が記述できれば、それを理想数と見なせるのではないかと考えられる。そして、もし、αが、すでに存在する数ならば、これは、要するに、{x∈R| x=α*w (w∈R)}、つまり、αの倍数の集合である。
これを通常(α)と書く。その代表的な性質を見てみると、次の三つがある:
要するには、αの倍数に、何かの数を倍すると、やはり倍数。倍数と倍数を足すと倍数、ということ。
それで、デーデキントは、この三つの性質をもつ、Rの集合を、Rの理想数の代わりだと見なして、イデアルと名付けた。
そして、数なので、それに対して、和や積などを次のように定義した。
また、素因数に対応する、素イデアルというものを、次のように定義した:
これは、二つの数の積 a*b が素数で割れたら、その素数は、a か b を割り切る、ということに対応する性質である。
そして、先の説明用の
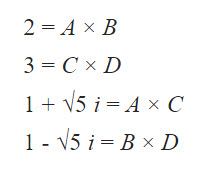
という四つの理想数A,B,C,Dの場合には、そのそれぞれを、
と特徴づけることができて、これを使い、理想数Aならば、2と1+√5iの「最大公約数」にあたるイデアル<2,1+√5>
<2,1+√5>={2*a+(1+√5i)*b|a,b∈R}
として明瞭簡単に定義できたのである。
デーデキントは、この様に、理想数の代わりに、集合であるイデアルというものを考えることにより、素因数分解の存在と一意性を、Rの様な代数的整数の体系について証明することに成功したのである。
そして、その後、彼は若き日に考えていた切断の概念を発表し、さらには、数学全体を、この切断やイデアルと似た集合で基礎づける方法を模索し始める。
続く…