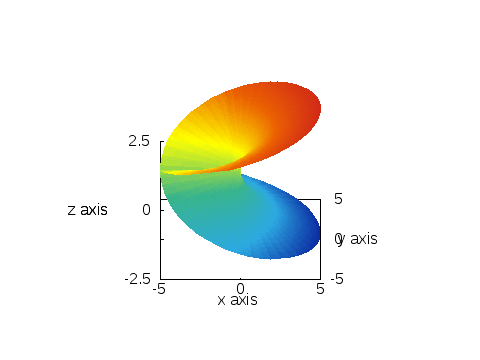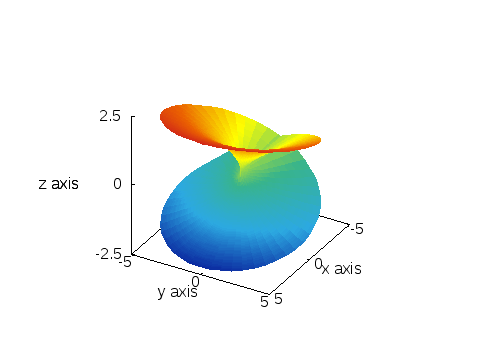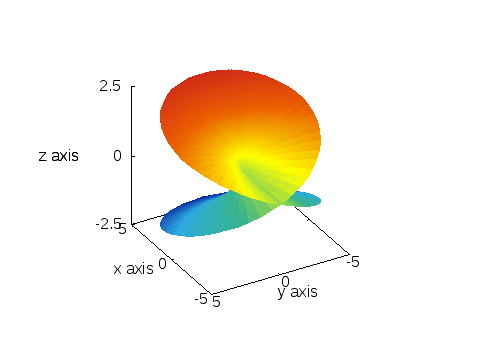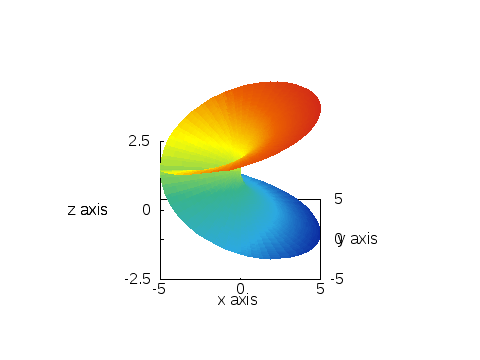2017年前期特殊講義 「数学の近代的基礎の歴史（１）」資料　 2017.05.22

質問票への回答の為の資料

  1. 前回「平方根のリーマン面」の形を説明しましたが、リーマン面は無限一つではなくて無限に多様です。前回見せたものは、√ｚ　という関数のリーマン面です。これが the リーマン面ではないので誤解しないようにしてください。たとえば、対数関数のリーマン面は、こんな感じです。
  2. リーマン面は、三次元空間に作図するのは不可能なものとのことでしたが、これを数学で扱う際は作図できなくてとも三次元空間にあるものとして（作図できるものと同じように）扱うのでしょうか？

前回までの資料より（√ｚ　とリーマン面の関係を前回は省略したが、それが理解を阻んでいると思われたので、その説明を追加）

構造主義では、実数、複素数などの皆さんに「馴染み深い数学存在」を相手にする、高校までの数学と大きく違っていて、具体的な数学対象の存在そのものより、その上の構造を重視する。

たとえば、体の理論では、（R1-R5）の公理を満たすものの研究がもっぱら行われ、順序と連続性（完備性）は、位相学（トポロジー）的構造だとみなされて、これと分離して研究されるのである。

マックス・ウェーバーの社会学で、経済システム、法システムに対して使われる、形式合理性、実質合理性という概念があるが、後に説明するように、この意味での形式合理性の数学における追及の一形態が構造主義だったのであり、先に説明した、内包、外延という言葉を使えば、高校までの数学は内包的であり、ブルバキ構造主義は外延的であるといえる。

このことは、後に詳しく再論するので、これはひとまず置いて、「構造主義」の別の典型である位相的構造の例を一つ見る。それが、歴史の話の第一歩となる、リーマンが考えた、リーマン面、多様体というものである。

まず、現代的な定義を、Wikipedia で見よう。

初めての人には難しすぎるので、もう少しわかりやすい位相空間というものの公理をみよう。

ちなみに、Wikpedia の説明からわかるように、位相空間＞多様体＞リーマン面という風に一般的である。つまり、リーマン面は、特殊な多様体であり、多様体は特殊な位相空間である。

この説明からわかるように、位相空間というのは、一つの集合Xであり、位相構造と呼ばれるものが、これもやはり集合の言葉を使って記述されている、開集合などにより付与されているのである。

おそらく、位相空間だけで、すでに初めての人には、複雑な構造に見えるだろうが、リーマン面というものは、さらにその上に、さまざまな複雑な構造が付与された、集合なのである。

しかし、それが19世紀初めに登場したとき、それは、集合の特性をすでに含みながらも、全く違う姿に見えたのである。

それは、まるで魔法かファンタジーの世界の存在のようであった。そして、その故に、後に集合論的なリーマン面の定義が、すでに名前がでているヘルマン・ワイルにより与えられたのである。

今でも、工学や物理学の学生に対してリーマン面を説明するときには、その19世紀のスタイルがとられることが多い。

そのやり方をつかって、このリーマン面がどんなものなのかを説明してみよう。

工学や物理学の講義でのリーマン面の説明：リーマンのオリジナルな説明

リーマン面は、ドイツの数学者ベルンハルト・リーマンが、彼の複素関数理論の中で生み出し、後の多様体論という幾何学理論に繋がった19-20世紀数学史上における非常に重要な概念。

それを非常に単純な場合である、平方根の場合に説明する。

２次関数y=x2の逆関数は、x=+√yと、x=-√yの２つがあり、これを y に対して、x が二つ決まる、つまり、+√y と -√y の両方が値となる「２値関数」とみる立場もある。

しかし、リーマンは、この x, y が複素数までに拡張されているときには、y が、２つの複素平面の上を動くと考え、その一枚では+√y を値として、もう一枚では -√yを値とすると考えると、値が一つの普通の関数になり、色々と数学的に都合が良いことを発見した。

ただし、その時、この２つの複素平面を「切り貼り」して、１枚の「面」にする必要があった。

そうやって出来たものが「平方根のリーマン面」である。

微分の概念は、複素関数、つまり、複素数を入力として、複素数を出力とする複素数の関数に拡張できるが、嘘を承知で言えば、その様な「微分可能な複素数の関数」の理論が、複素関数論。

その複素関数論では、平方根とか、あるいは対数とか、ある微分可能な複素数の関数の逆関数で重要なものが沢山ある。

それらの多くは、値が沢山ある多値関数なのだが、それを一値にする手法がリーマン面。

それは、単に「一値にできる」というようなことでなく、そういうリーマン面の幾何学的特性で、実に色々なことが分かる理論であった。

ともかく、平方根のリーマン面というのは、次のような「形」をしている「面」：



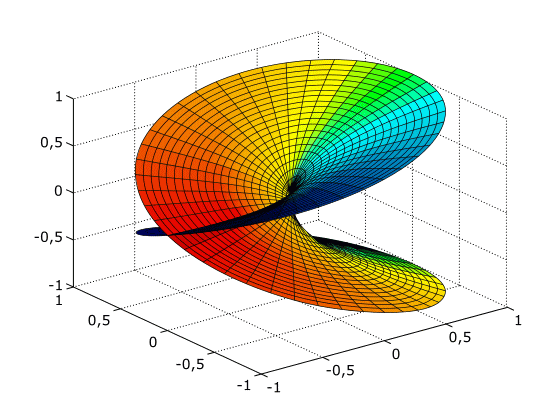
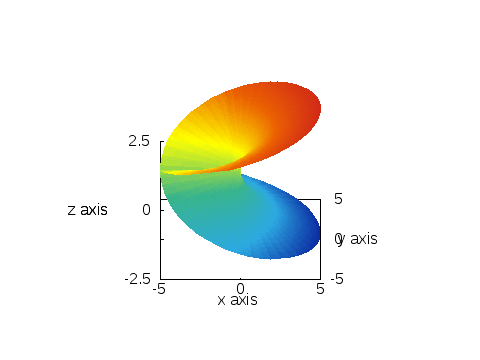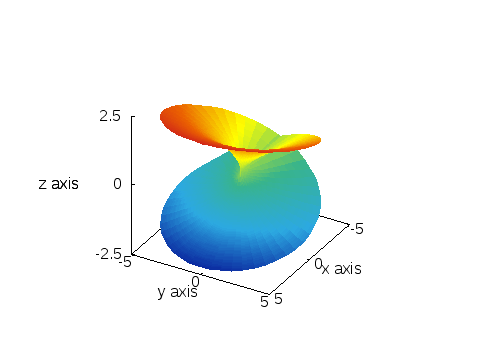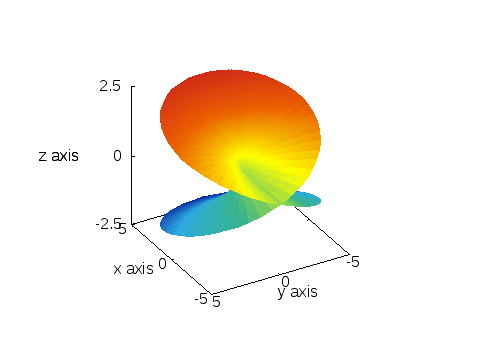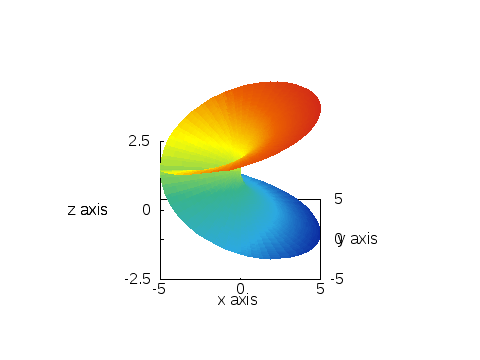
ポイントは、面が自分自身を横断している点。

正確にいうと、「横断している様に見えるだけで、本当は横断してない」と考える。

実は、このリーマン面は三次元空間の曲面として作図するのは不可能なもので、それを無理矢理描くために、このように面が面を横断してしまう。

その作り方は、次のようにする：

平方根のリーマン面の作り方

簡単に動画を説明すると、２つの円盤を用意し（それが２つの複素平面だと思う）、中心から切り込みを入れる。
そして、その切り込みの（すぐ）上の面を、もう一つの円盤の切り込みの（すぐ）下の面に繋ぐ。
つまり、〇がついた二つの切り口同士を、×がついた二つの切り口同士を繋ぐことを試みる。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。

２つの円盤に上の面と下の面があるので、総計４面あるが、ひとつの円盤Aの上の面をもう一つの円盤Bの下の面に繋ぐと、それが邪魔して、最初の円盤Aの下の面を、もう一つの円盤B上の面につなぐことはできない。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。

しかし、それを無理矢理できた、と思うために、〇印の二つの切り口を繋いでいるピンクのテープ（PostIt)を半分に切って、それぞれを、X印の切り口に透明テープではりつける。 



動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、動画をダウンロードしてみてください。ダウンロード1,?ダウンロード２

こうやって作った面のモデルが、先の図、つまり、次のものと同じだとわかるだろうか？動画の最後のあたりの画像と、下の画像を見比べてみてください：?

この平方根のリーマン面が、持つ不思議な性質の一つとして「原点」、つまり、円盤の中心のことなのだが、その周りを連続に回って元いた点に戻ろうとすると、普通の平面ならば、360度、つまり、1回転で元に戻るが、このリーマン面では、2回転しないと元に戻らないという性質がある。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。


こういう性質は、少しなれると図を見て直観的に理解することができるようになる。後で説明するが、リーマンは、こういう仮想的な面を使うと、複雑な計算の末にようやくやわかるような事実が、図形（リーマン面）についての幾何学的直観で理解できることを発見し、また、さらには、この面の幾何学的性質と、この面を定義域にする数学的に性質の良い関数の全体の間に、大変面白い関係があることなどを発見した。?

追加の説明：

以上の説明は、非常に不完全なものなので（例えば、紙切り細工で作ったリーマン面上で、どのように√ｚの値を定めるか説明していない。実は、数学的には、これが一番肝心、詳しくは、これらの、東大の物理工学科、九大の物理学科の講義ノートを参考にして欲しいが、何故、二面の円盤の切り口を、動画のように「交叉」して張り付けるかを以下に簡単に説明しておく。まずは複素数の説明から。

複素数と複素平面

複素数というものは、虚数単位 i という新しい数を実数の体に追加してできる数。虚数単位は二乗すると -1 となる数。つまり、i^2=-1。x^2=-1 という方程式は、x が実数だと解けないが、i があれば、この方程式の解は、i と -i だと考えることができる。複素数とは、x+iy (x, y は実数）あるいは、同じことだが x+yi という形の数のことで、その全体の集合が、実数の全体の集合の場合のように体となるもの。

高校までで学習する体の例として、実数係数の有理式（分数式）の全体がある。（参考１，２）　これが体になることは、簡単に確認できるので自分でやってみると良い。

複素数は、虚数単位を有理式の変数 x だとおもって（つまり、記号が違うだけとみなす）、一つの有理式だと思えばよい。ただし、唯一違うこととして、i^2=-1　という法則（公理）を使ってよいとする。

この法則i^2=-1のお陰で、このサイトの「除法」のところで、例を使って説明されているように、5-6i/3+2i のような分数式は、分母・分子に 3-2i （3+2iの共役）をかけることにより、3/13-(28/13)i という、x+yi の形になる。そのため有理式とちがって、複素数を表す時には分数を使わないで済ませることができる。

実数係数の方程式は、例えば、x^2=-1 の様に実数解を持たないものがある。しかし、複素数を係数とする方程式は、必ず複素数の解を持つ。このことが複素数を、数学的には、実数より遥かに「良い」ものにしている。

ドイツの数学者ガウスは、この x + i y という複素数の「形式」を、(x, y) という座標と見なし、複素数の全体とは、二次元平面だと考えた。この様に複素数の全体と同一視された平面を複素平面という。

一つの複素数　x + i y　が、平面上の点 (x,y) と見なされるようになると、　複素数を「表現」する別の方法が見出される、それが複素数の極形式。

そして、この極形式を使うと、複素数の平方根√z は、このページの、この部分で説明されているように、ｚ　が r(cosθ+i sinθ) の時、√z は、 √r(cos（θ/2)+i sin(θ/2)) になる。

実は、√ｚ　のリーマン面のモデルを紙切り細工で作るときに、2枚のシートを用意したのは、この√ｚ　の式の cos（θ/2), sin(θ/2)の部分に秘密がある。

√z ＝ √r(cos（θ/2)+i sin(θ/2)) 　の　ｒ　は固定して、θだけを変化させてみる。

θを、0から2π（360度）まで変化させると、cosθ, sinθならば値が元に戻る。しかし、cos（θ/2), sin(θ/2) だと、θ/2 が0からπまでしか変化しない。そして、cos(θ+π)=-cos（θ）, sin(θ+π)=-sin（θ）となる。（参考）

つまり、θが２で割られているために、θを0から４π（720度）まで変化させて、漸く、√ｚ　の値は元に戻る。

という動画で、林が中心と二回り、つまり、4π移動する様に線を描いたのは、このθの変化を表現したもの。

注意：ただし、林は時計廻りに円を描いている。数学では反時計回りに角度を決めるので、正確に言えば、林は、θを　０から-４πまで動かしている。つまり、ここで書いている説明の数値に全部マイナスをつけた場合のビデオになっている。このビデオを作ったときには、値の決め方の説明までするつもりがなかったので、いい加減になってしまった。すみません。（＾＾；）　ここで書いている説明に対応させるには、頭の中でビデオ

東大の物理工学科、九大の物理学科の講義ノートの説明にあるように、√ｚ　の、そのリーマン面上での値の定義は、ｚ= r(cosθ+i sinθ)のθが、０から2πの間、つまり、一枚目を一周する間は、√r(cos（θ/2)+i sin(θ/2)) にする。

そして、2周目、つまり、θが2πから4πの間は、もう一つのシートに移動して、そちらを新しい複素平面だと考える。そうすると、二周目では、√r(cos（θ/2)+i sin(θ/2)) 　の値が、一枚目の複素平面の対応する複素数の関数値の丁度　－１　倍になることがわかる。

たとえば、一枚目の複素平面（シート）上の、θ＝πの複素数は、z=r(cosθ+i sinθ)=r(cosπ+i sinπ)=-r であり、その平方根の値　√r(cos（θ/2)+i sin(θ/2))　は　√r i 　となるが、二枚目の複素平面では、この -r に当たる位置の複素数は、2周目なのでθ=π＋2πの複素数だと考えて、z=r(cosθ+i sinθ)=r(cos3π+i sin3π)とする。

そうすると、その平方根の値　√r(cos（θ/2)+i sin(θ/2))　は　r(cos(π/2+π）+i sin(π/2+π）)になる。

ところが、cos(θ+π)=-cos（θ）, sin(θ+π)=-sin（θ）　なので、一枚目の対応する位置の複素数の平方根の-1倍だとわかる。

つまり、2枚の複素平面は、二つある平方根　±√ｚ　の内、＋√ｚ　の方が1枚目を定義域にしていて、‐√ｚ　の方が2枚目を定義域にしていると考えると丁度この「二周回り」の現象とピッタリ合うことになり、しかも、プラスとマイナスで定義域を分けたので、2値関数が１値関数になる。

リーマンは、この様に考えて、二つのシート（複素平面）を、画像や動画で見せたような形でくっつけたのである。

練習問題：　くっつけた所（切断線）の上で、＋√ｚ　と ‐√ｚ　が同じ値でないと関数が連続でなくなる。実際には連続になっている。どうしてか考えてみてください。これが分かればリーマンの発想の元が理解できるようになるはずです。

リーマン面の方法と19世紀のドイツ数学

リーマンの概念数学

この部分の参考文献

  1. 上野健爾　「リーマンが変えた数学」、雑誌「現代思想」、総特集「リーマン」、2016年3月臨時増刊号収録
    注：この「現代思想」、総特集「リーマン」、2016年3月臨時増刊号の他の文献にも、林が共著者である八杉の文献など、この講義を理解するために参考になるものがある。
  2. リーマン論文集、足立他訳、数学史叢書、朝倉書店
  3. Riemann の論文を集めたサイト
    注. 学術誌に発表されたものは、オリジナルを、ゲッチンゲン大学のWEBアーカイブで閲覧・ダウンロード（無料）できる。

以下では、この参考文献１－３を、それぞれ[上野], [論文集] ,[PAPERS]と、また、３で触れたゲッチンゲンのアーカイブを[GDZ]と表記する。

リーマンが、リーマン面の概念を発表したのは、1851年の学位論文だった。この論文で、リーマンは、フランスの数学者コーシーにより開拓されたばかりの最新の数学理論「複素関数論」（参考）を、リーマン面のアイデアを使って刷新してみせた。（[上野]参照）。

このリーマン面を使う新しい方法の威力を見せつけたのが、クンマーというドイツの数学者が1835年に発表した

という題名の論文（[GDZ]の該当文献へのリンク, ＊)の結果を拡張した1857の論文([PAPERS]の Beitrage zur Theorie der durch die Gauss'sche Reihe F(a,b,c,x) darstellbaren Functionen (Abhandlungen der Koniglichen Gesellschaft der Wissenschaften zu Gottingen, 7 (1857))。

題名中に、複雑な数式が書かれていることが、それを象徴しているが、このクンマーの論文は、大量の数式と計算に満ちていた。 リーマンは、リーマン面やP関数とよばれるものを用いる概念的な方法で、必要な計算と数式の複雑度を大幅に低減できることを示した。

注意：もちろんリーマンの方法でも、多くの数式や計算が用いられている。飽くまで比較の問題。ただし、リーマンの方法だと、P関数と呼ばれるものが、ある意味で、幾何学の証明の補助線のような役割をして、全体の見通しが非常によくなっていた。

リーマンの数学的方法の特徴は、問題を解くために、リーマン面のような新しい概念を、その存在の問題を気にせずに導入し、それを用いて、問題を考え、解く所にあった。

これがデーデキントやヒルベルトに継承され、ゲッチンゲン大学の数学の伝統となり、それが20世紀の構造主義につながった。

一方で、ゲッチンゲンとともに、ドイツ数学の中心地だったベルリン大学では、数式と計算が重んじられ、リーマン面のような、あやふやな概念、空想の産物を、数学において使うことは嫌われた。

そのため、リーマンの数学も、ベルリンでは、不確かなものと考えられていた。実際、リーマンの複素関数の理論で重要な役割を果たす、ディリクレ原理というものは、リーマン面に対する物理的直観で導き出されたと考えられているが、ワイエルシュトラスという、ベルリン大学の数学者により、非常に単純な反例を与えられてしまった。

そのワイエルシュトラスとともに、ベルリン大学の数学を代表したのが、先にでてきたクンマー、そして、その弟子のクロネッカーである。

そして、数学の近代的基礎の歴史は、このベルリンとゲッチンゲンの「対立」をめぐって展開することになる。

 ここから今回の資料

 「構造主義の源流」としてのリーマン

切断を考えたデーデキントの数学が、構造主義の最も重要な源流であったことは、多くの数学史家や数学者が認めているところである。

たとえば、ブルバキの構造主義代数学の直接の先祖は、ゲッチンゲン大学のE.ネーターとその弟子たちの数学だが、そのネーターは、「すべてがすでにデーデキントにある」 Es steht alles schon bei Dedekind と言ったというのは、有名な話である。

ブルバキ構造主義の元となった19世紀の数学には、デーデキントのものだけではなく、イギリス抽象代数学派など、色々あった。しかし、源流として最も大きかったのはデーデキントであろう。

しかし、そのデーデキントは、彼のやり方の源流、少なくとも、哲学的・思想的な源流は、彼の年長の友人リーマンにあると考えていたらしい。

実際には、デーデキントの数学とリーマンの数学は、かなり違うものである。デーデキントの数学は、友人であり畏敬する「師」でもあるリーマンの数学の「理解し難い天才的直観」を、平均的数学者でも理解できるものに置き換えることにより生まれたとも考えられる。

このリーマンと、デーデキントの数学の末裔である構造主義の数学を比較しつつ、なぜ、リーマンが集合論の源流だ、と言われるようになってきたのかを説明する。

√z のリーマン面は、まだ、構造主義とはいえない。構造主義では、数学的対象は、その実体を無視して、例えば体の公理のように、「あるとせよ」として「定義」される。

それに対して、リーマン面は、この世に存在しないような想像力の産物だが、複素平面という、この世に存在する「材料」から作られていた。

もし、ここでリーマンがとどまっていたら、リーマンが集合論の源流とか、構造主義数学の源流と呼ばれるようにはならなかっただろう。

注. ただし、「概念で考える数学」　Denken in Begriffen, Thinking in concepts　の源流とは看做されたかもしれない。

幾何学の基礎をなす仮説について

リーマンが、集合論の源流とか、構造主義数学の源流と呼ばれるようになった根拠は、彼の教授資格論文であり、生前は未出版で、デーデキントによりその死後に出版されることになった Ueber die Hypothesen, welche der Geometrie zu Grunde liegen 幾何学の基礎をなす仮説について、である。

この論文は、数学の論文なのだが、殆ど数式がない。デーデキントの Habilitation は、さらに数式がなく、数式らしきものは　「半径=1の円」という表現だけなので、これは当時は数学が哲学の学部の中にあったことが影響したのかもしれないが、Herbart という哲学者の名前がでてくるなど、リーマン自身が非常に哲学的内容を意識していたのは確かである。実際、彼は自分を自然哲学者だと考えていたらしい。

注．リーマンへのヘルバルトの影響については、色々な説があり、ゲッチンゲン大学図書館のリーマンの遺稿調査で知られるショルツが、直接の影響がなかったとしたので有名。しかし、いろいろな資料的証拠などから、現在は、あったとする説の方が主流だろう。その経緯は、この論文を参照。本講義の重要な背景である Laugwitz, Ferreiros　の両著書（5月8日の講義資料を参照）でも影響が主張されており、本講義では、あったという立場に立つ。）

この「幾何学の基礎をなす仮説について」で、初めて数学の世界に導入されたのが、構造主義数学の例として説明した多様体の概念である。

この多様体は、これまでの講義資料では、次のようにリーマン面の現代的説明の中で登場している：

まず、現代的な（リーマン面の）定義を、Wikipedia で見よう。
初めての人には難しすぎるので、もう少しわかりやすい位相空間というものの公理をみよう。
ちなみに、Wikpedia の説明からわかるように、位相空間＞多様体＞リーマン面という風に一般的である。つまり、リーマン面は、特殊な多様体であり、多様体は特殊な位相空間である。
この説明からわかるように、位相空間というのは、一つの集合Xであり、位相構造と呼ばれるものが、これもやはり集合の言葉を使って記述されている、開集合などにより付与されているのである。

多様体の原語は、Mannigfaltigkeit　で、その本来の意味は、多様さ、多様性であるが、今では、これが数学用語として幾何学的な空間を表すものとして使われている。

しかし、実は、この用語は、古い歴史観（あるいは一般的歴史観）では、集合論の祖とされるカントールが、集合を意味して使っていた用語でもある。そして、その用語は、デーデキントが、リーマンがそれを使っていたので、使うと良いと、カントールに書簡で勧めていることが知られている（Ferreiros pp.39-40参照）。しかし、結局、カントールの用語は、現在も使われる Menge に落ち着くこととなった。

この20世紀数学への影響力が非常に強く、また、同時に曖昧で難解な短い論文で、リーマンは、√ｚ　のリーマン面を彼が構成した時と異なり、現代の構造主義のように、何もない白紙として多様体について語った。

つまり、既存、別の言い方をすれば、その時代に既に数学の対象であるとされていたものから何かを作るのではなくて、多様体というものがあり、その上に、これこれの構造があるという風に語ったのである。

この時代、まだ、位相空間諭というものは無く、上で示した現代的な多様体の定義はできていない。それが現れるのは、およそ60年後の1913年に出版されたヘルマン・ワイルの Die Idee der Riemannische Flaeche リーマン面の概念、でである。

しかし、リーマンは、すでに抽象的に導入された多様体の上に、「計量」という長さや角度を与えるための抽象的構造を追加して、この多様体を連続な局面のように考えるというアイデアを述べており、これが構造主義の嚆矢とされる大きな理由となっている。

また、リーマンは、離散的な多様体という言葉を使っている。これが何なのかは、史料的に推定する材料がなく、色々な説があるが、一つの説が、これが後の集合と同じものだったのではないかという説である。

その理由は、リーマンが連続な多様体には計量で量を測るが、離散的多様体では、数え上げることにより量が測られる、つまり、個数で離散的多様体を特徴づけていることがある。また、デーデキントのカントールへの名称の示唆も、すくなくとも、リーマンと最も親しかった数学者が、リーマンが多様体で集合一般を表していたと考えていたらしいことを示している。

このリーマンの論文は、難解するぎるので、これ位に留め、次に、このリーマンからデーデキントが、どの様に思想を継承し、また、変えていったかについて述べる。

非常に興味深いことに、集合論の祖の一人としてのデーデキントには、リーマン以外にもう一人の源泉がいた。それが、先に、リーマンが彼の概念的数学で、その数学的業績を軽々と乗り越えたと説明した、クンマーというベルリンの数学者の代数学・数論である理想数の理論であった。