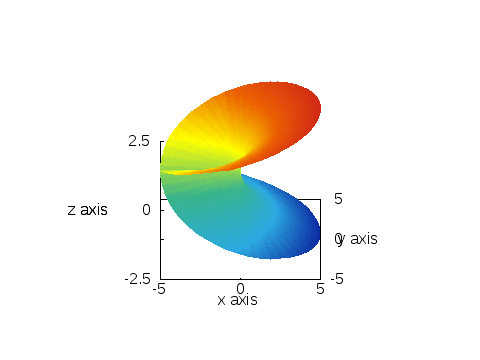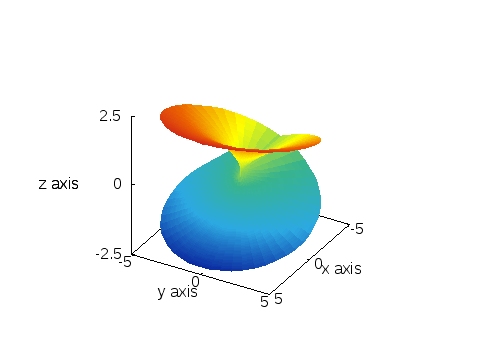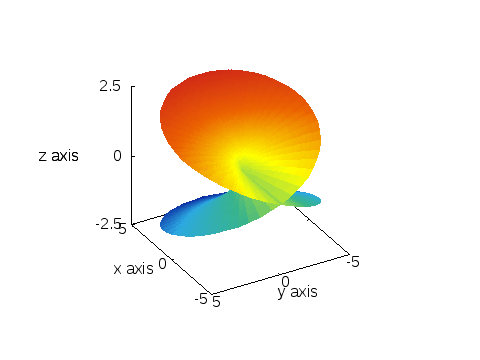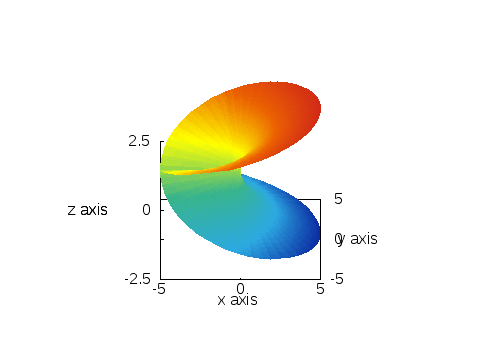2017年前期特殊講義 「数学の近代的基礎の歴史（１）」資料　 2017.05.15

5月16日に、講義中に見つけたリンクの間違いの修正と、工学部（東大）、理学部物理（九大）でのリーマン面を説明する講義資料の追加を行った。

平方根のリーマン面の分かり易い動画GIF画像が見つかったので、5月21日に追加した。

質問票への回答の為の資料

1. 「構造主義」の「構造」から「何からできているかということ」を連想した人がいましたが、この「構造」のイメージあるいは意図は、「社会構造」というときの「構造」ですので、「システムを構成しているものの関係性」という感じです。参照： Wikipedia の「社会構造」。

前回の資料より

現代の純粋数学のスタイル＝構造的主義

構造主義という言葉は、例えば文化人類学者クロード・レヴィ＝ストロースの思想としても知られている幅広い学問的傾向の名称である。

そのレヴィ＝ストロースの有名な業績に未開社会の親族構造の研究があり、これに群論という数学の理論が使われている。

この研究の群論的部分を実際におこなったのは、これ以後の講義に何度も登場することになる、哲学者シモーヌ・ヴェイユの兄で20世紀を代表する数学者の一人アンドレ・ヴェイユである。

このヴェイユが中心的な発起人として1930年代に立ち上げたフランスの若手数学者集団のペンネームが二コラ・ブルバキであり、この集団をブルバキといい、そのメンバーをブルバキストという。

この集団の目的は1930年代には、ドイツに比べて、いかにも古臭かったフランスの数学高等教育を刷新できるような解析学の教科書を書くことだった。

その後、教科書のスコープは、広く純粋数学一般に広げられ、「ブルバキ数学原論」と呼ばれた。

ちなみに、先にブルバキ構造主義数学を「呼ばれていたもの」と過去形で書いたのは、これがあまりに常識化してしまって、特別な名前で呼ぶ必要がなくなっているからだといえる。

注意：この二コラ・ブルバキの Wikipedia 記事にあるように、カテゴリー論というものが普及してきて、これの登場以前にスタイルが確定したブルバキ数学原論のスタイルが古臭くなっている面がある。それを根拠にブルバキ構造主義が廃れたかのように言う人がいるが、これは間違いである。カテゴリー論は、ブルバキの意味での構造の表現・研究のためのスタイルの一つであり、これによりブルバキ構造主が廃れたのではなく、むしろカテゴリー論の手法により、ブルバキ構造主義の理念が進化したのである。実際、カテゴリーだけを使い、ブルバキの様に集合を使わないことは可能なのだが、かえってわかりにくくなってしまう。そのため、Wikipedia 記事にあるGrothendieck の代数幾何学が典型だが、ブルバキ原論的な記述とカテゴリー論的記述が併用されるのが、通常のスタイルである。

ブルバキ構造主義数学は、実質的には、それ以前に、特にドイツを中心にして存在していたといえる。それがブルバキの数学原論シリーズと、それに伴う彼らの普及活動と、そして、その普及活動の中で、「構造」というこのスタイルの意味を明瞭に説明するための理念が生み出されたため、これにブルバキという名称がついているのである。

その「構造」という概念は、実は、すでに講義の中で出てきている。例えば、大阪大の資料

http://www.math.sci.osaka-u.ac.jp/~matsumoto/lectures/2016-fs1/docs/2016-fs1-09.pdf

に、体というものがあったが、これが代数的構造の典型例である。

その資料の説明では、まず、R　という集合があり、その要素のひとつひとつがどう出来ているかには、何も言及せず、Rの上の演算を導入して（R1)、それについての条件（R2-5)が「公理」として記述されていた。

これを数学では「Rという集合の上に、体と呼ばれる「代数構造」（「代数的構造」）が導入された」という。

この様に、真っ新なキャンバスとして集合が用意され、その上に、体の場合の演算 a+b, ab などのような「構造」を導入して、それを数学の対象として考える、それが構造主義である。

実数の定義の公理的方法では、その公理を満たすRとR'があったら、その間に両者を「同じと看做すための写像」が存在することが示され、それにより、唯一の存在であるはずの「実数の全体」というものがあると看做された。

こういうことが成り立つ公理系（公理の集まり）は、univalent とか categorical と呼ばれるが、体の公理系（R1-R5）は、そうではない。

実際、有理数の全体、実数の全体、複素数の全体は、みな、この公理系を満たす。

構造主義では、実数、複素数などの皆さんに「馴染み深い数学存在」を相手にする、高校までの数学と大きく違っていて、具体的な数学対象の存在そのものより、その上の構造を重視する。

たとえば、体の理論では、（R1-R5）の公理を満たすものの研究がもっぱら行われ、順序と連続性（完備性）は、位相学（トポロジー）的構造だとみなされて、これと分離して研究されるのである。

マックス・ウェーバーの社会学で、経済システム、法システムに対して使われる、形式合理性、実質合理性という概念があるが、後に説明するように、この意味での形式合理性の数学における追及の一形態が構造主義だったのであり、先に説明した、内包、外延という言葉を使えば、高校までの数学は内包的であり、ブルバキ構造主義は外延的であるといえる。

このことは、後に詳しく再論するので、これはひとまず置いて、「構造主義」の別の典型である位相的構造の例を一つ見る。それが、歴史の話の第一歩となる、リーマンが考えた、リーマン面、多様体というものである。

まず、現代的な定義を、Wikipedia で見よう。

• リーマン面
• 多様体

初めての人には難しすぎるので、もう少しわかりやすい位相空間というものの公理をみよう。

ちなみに、Wikpedia の説明からわかるように、位相空間＞多様体＞リーマン面という風に一般的である。つまり、リーマン面は、特殊な多様体であり、多様体は特殊な位相空間である。

• 位相空間

この説明からわかるように、位相空間というのは、一つの集合Xであり、位相構造と呼ばれるものが、これもやはり集合の言葉を使って記述されている、開集合などにより付与されているのである。

おそらく、位相空間だけで、すでに初めての人には、複雑な構造に見えるだろうが、リーマン面というものは、さらにその上に、さまざまな複雑な構造が付与された、集合なのである。

しかし、それが19世紀初めに登場したとき、それは、集合の特性をすでに含みながらも、全く違う姿に見えたのである。

それは、まるで魔法かファンタジーの世界の存在のようであった。そして、その故に、後に集合論的なリーマン面の定義が、すでに名前がでているヘルマン・ワイルにより与えられたのである。

今でも、工学や物理学の学生に対してリーマン面を説明するときには、その19世紀のスタイルがとられることが多い。

そのやり方をつかって、このリーマン面がどんなものなのかを説明してみよう。

工学や物理学の講義でのリーマン面の説明：リーマンのオリジナルな説明

リーマン面は、ドイツの数学者ベルンハルト・リーマンが、彼の複素関数理論の中で生み出し、後の多様体論という幾何学理論に繋がった19-20世紀数学史上における非常に重要な概念。

それを非常に単純な場合である、平方根の場合に説明する。

２次関数y=x2の逆関数は、x=+√yと、x=-√yの２つがあり、これを y に対して、x が二つ決まる、つまり、+√y と -√y の両方が値となる「２値関数」とみる立場もある。

しかし、リーマンは、この x, y が複素数までに拡張されているときには、y が、２つの複素平面の上を動くと考え、その一枚では+√y を値として、もう一枚では -√yを値とすると考えると、値が一つの普通の関数になり、色々と数学的に都合が良いことを発見した。

ただし、その時、この２つの複素平面を「切り貼り」して、１枚の「面」にする必要があった。

そうやって出来たものが「平方根のリーマン面」である。

微分の概念は、複素関数、つまり、複素数を入力として、複素数を出力とする複素数の関数に拡張できるが、嘘を承知で言えば、その様な「微分可能な複素数の関数」の理論が、複素関数論。

その複素関数論では、平方根とか、あるいは対数とか、ある微分可能な複素数の関数の逆関数で重要なものが沢山ある。

それらの多くは、値が沢山ある多値関数なのだが、それを一値にする手法がリーマン面。

それは、単に「一値にできる」というようなことでなく、そういうリーマン面の幾何学的特性で、実に色々なことが分かる理論であった。

ともかく、平方根のリーマン面というのは、次のような「形」をしている「面」：

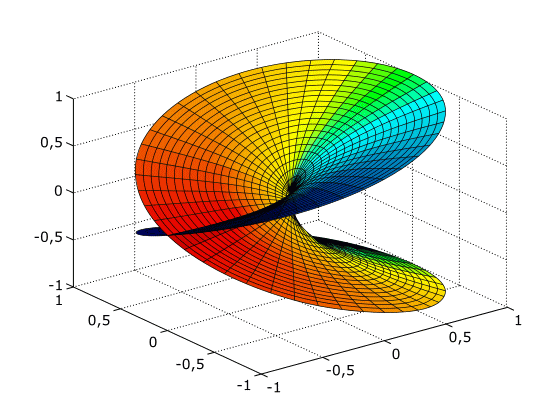
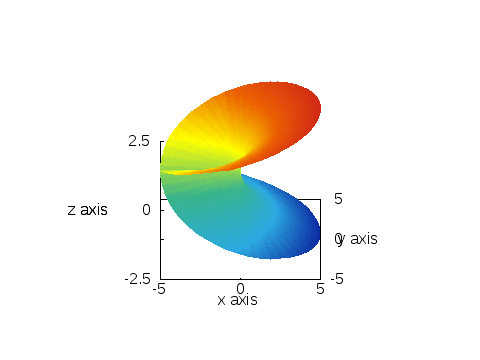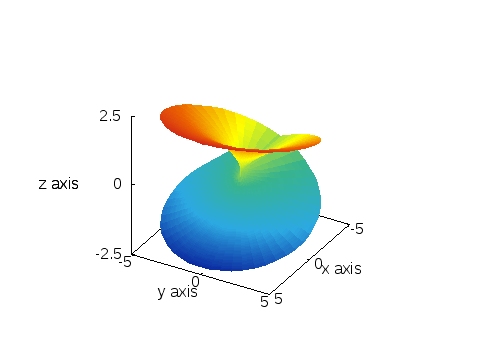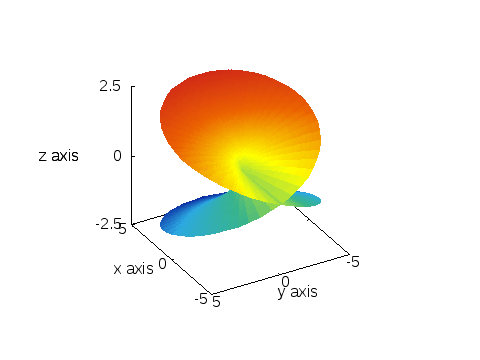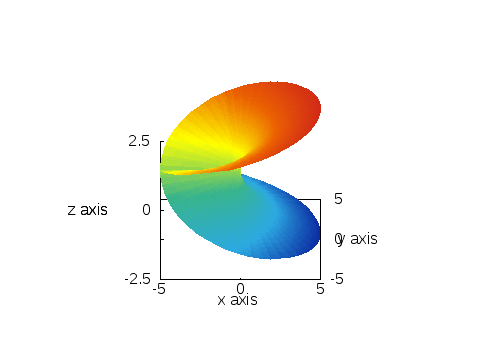
ポイントは、面が自分自身を横断している点。

正確にいうと、「横断している様に見えるだけで、本当は横断してない」と考える。

実は、このリーマン面は三次元空間の曲面として作図するのは不可能なもので、それを無理矢理描くために、このように面が面を横断してしまう。

その作り方は、次のようにする：

平方根のリーマン面の作り方

簡単に動画を説明すると、２つの円盤を用意し（それが２つの複素平面だと思う）、中心から切り込みを入れる。
そして、その切り込みの（すぐ）上の面を、もう一つの円盤の切り込みの（すぐ）下の面に繋ぐ。
つまり、〇がついた二つの切り口同士を、×がついた二つの切り口同士を繋ぐことを試みる。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。

２つの円盤に上の面と下の面があるので、総計４面あるが、ひとつの円盤Aの上の面をもう一つの円盤Bの下の面に繋ぐと、それが邪魔して、最初の円盤Aの下の面を、もう一つの円盤B上の面につなぐことはできない。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。

しかし、それを無理矢理できた、と思うために、〇印の二つの切り口を繋いでいるピンクのテープ（PostIt)を半分に切って、それぞれを、X印の切り口に透明テープではりつける。 



動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、動画をダウンロードしてみてください。ダウンロード1,?ダウンロード２

こうやって作った面のモデルが、先の図、つまり、次のものと同じだとわかるだろうか？動画の最後のあたりの画像と、下の画像を見比べてみてください：?

この平方根のリーマン面が、持つ不思議な性質の一つとして「原点」、つまり、円盤の中心のことなのだが、その周りを連続に回って元いた点に戻ろうとすると、普通の平面ならば、360度、つまり、1回転で元に戻るが、このリーマン面では、2回転しないと元に戻らないという性質がある。


動画を再生するにはvideoタグをサポートしたブラウザが必要です. 非対応ブラウザの場合は、ダウンロードしてみてください。

以上の説明は、非常に不完全なものなので（例えば、紙切り細工で作ったリーマン面上で、どのように√ｚの値を定めるか説明していない。実は、数学的には、これが一番肝心だが、複素数の指数関数の知識が必要なので省略した）、詳しくは、東大、九大の次の講義ノートを参考にしてほしい：東大の物理工学科、九大の物理学科

ここから今回の資料

リーマン面の方法と19世紀のドイツ数学

リーマンの概念数学

この部分の参考文献

1. 上野健爾　「リーマンが変えた数学」、雑誌「現代思想」、総特集「リーマン」、2016年3月臨時増刊号収録
   注：この「現代思想」、総特集「リーマン」、2016年3月臨時増刊号の他の文献にも、林が共著者である八杉の文献など、この講義を理解するために参考になるものがある。
2. リーマン論文集、足立他訳、数学史叢書、朝倉書店
3. Riemann の論文を集めたサイト
   注. 学術誌に発表されたものは、オリジナルを、ゲッチンゲン大学のWEBアーカイブで閲覧・ダウンロード（無料）できる。

以下では、この参考文献１－３を、それぞれ[上野], [論文集] ,[PAPERS]と、また、３で触れたゲッチンゲンのアーカイブを[GDZ]と表記する。

リーマンが、リーマン面の概念を発表したのは、1851年の学位論文だった。この論文で、リーマンは、フランスの数学者コーシーにより開拓されたばかりの最新の数学理論「複素関数論」（参考）を、リーマン面のアイデアを使って刷新してみせた。（[上野]参照）。

このリーマン面を使う新しい方法の威力を見せつけたのが、クンマーというドイツの数学者が1835年に発表した

という題名の論文（[GDZ]の該当文献へのリンク, ＊)の結果を拡張した1857の論文([PAPERS]の Beitrage zur Theorie der durch die Gauss'sche Reihe F(a,b,c,x) darstellbaren Functionen (Abhandlungen der Koniglichen Gesellschaft der Wissenschaften zu Gottingen, 7 (1857))。

題名中に、複雑な数式が書かれていることが、それを象徴しているが、このクンマーの論文は、大量の数式と計算に満ちていた。 リーマンは、リーマン面やP関数とよばれるものを用いる概念的な方法で、必要な計算と数式の複雑度を大幅に低減できることを示した。

注意：もちろんリーマンの方法でも、多くの数式や計算が用いられている。飽くまで比較の問題。ただし、リーマンの方法だと、P関数と呼ばれるものが、ある意味で、幾何学の証明の補助線のような役割をして、全体の見通しが非常によくなっていた。

リーマンの数学的方法の特徴は、問題を解くために、リーマン面のような新しい概念を、その存在の問題を気にせずに導入し、それを用いて、問題を考え、解く所にあった。

これがデーデキントやヒルベルトに継承され、ゲッチンゲン大学の数学の伝統となり、それが20世紀の構造主義につながった。

一方で、ゲッチンゲンとともに、ドイツ数学の中心地だったベルリン大学では、数式と計算が重んじられ、リーマン面のような、あやふやな概念、空想の産物を、数学において使うことは嫌われた。

そのため、リーマンの数学も、ベルリンでは、不確かなものと考えられていた。実際、リーマンの複素関数の理論で重要な役割を果たす、ディリクレ原理というものは、リーマン面に対する物理的直観で導き出されたと考えられているが、ワイエルシュトラスという、ベルリン大学の数学者により、非常に単純な反例を与えられてしまった。

そのワイエルシュトラスとともに、ベルリン大学の数学を代表したのが、先にでてきたクンマー、そして、その弟子のクロネッカーである。

そして、数学の近代的基礎の歴史は、このベルリンとゲッチンゲンの「対立」をめぐって展開することになる。