の定義である、

を、「論理の部分」である
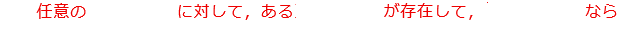
と「数の部分」である

に分けた。
デーデキントは、イデアルと同じような方法で、実数を有理数と集合を使って定義した。そして、さらには集合だけを使って自然数さえも定義した。
これらの業績から、デーデキントは、集合についての数学理論である集合論、特に、数学の基礎づけに使われる集合論や、数学の研究のために使われる集合論のパイオニアと見なされている。
しかし、デーデキントが開拓した集合論は、数学を行うために作られており、デーデキントは、、集合論という独立した研究分野は、もう一人のパイオニア、ゲオルグ・カントルが開拓した。
日本語の Wikipedia の記事でもそうだが、カントルはカントールとも表記される。しかし、ドイツ語の Cantor の発音に近い日本語表記は、カントワかカントアである。発音サイト Forvo での Cantor。
しかし、既に、カントル、カントールという表記が定着しており、カントワと書くと違和感を持つ人が多いと思うので、より近いカントルという表記を使っている。
ちなみに、Dedekind を、デーデキントと表記しているが、これをデデキントと表記する人もいる。Forvo で見てみると、僅かにデーデキントの方が近いように思える。
後で出て来る、これもドイツの数学者、David Hilbert は、ドイツ語で、v を英語の f のように発音することから、ダーフィット・ヒルベルトと書かれることが多いのだが、David はヘブライ由来の名前であるため、例外として、v は濁音になる。そのため、ダービット、あるいは、ダーヴィットと表記する方が良いと思われる。
デーデキント(1831-1916)が彼の切断の理論を発表した同じ1872年、同じドイツの数学者カントル(1845-1918)が、やはり実数を定義した。カントールの方法は、有理数の切断を使うデーデキントのものと違い、有理数の収束する列を使うものだった。
この共通の仕事を通して、この両者は連絡を取り合いながら集合論を開拓していくこととなった。しかし、その方向性は大きく違っていた。
デーデキントが、集合を使ったのは、実数を定義する(切断)、代数的整数論を行う(イデアル)のように、数学を記述するためだった。つまり、デーデキントの集合論は数学を行うための「手段としての集合論」「道具としての集合論」だった。
これに反し、カントールが開拓した集合論は、それ自身が数学の理論として研究する価値があるような、「目的としての集合論」であった。
集合は、高校での数学でも教えられているが、集合についてだけの問題が、入試問題として出題されることは、稀である。
集合は、あまりに単純で、何の構造も持たない様に見えるので、デーデキントの様に、道具として使うならば別だが、これについての「理論」などというものは出来そうにないように見える。
しかし、カントルは、デーデキントも用いた関数、あるいは、写像(デーデキントは写像 Abbildung と呼んだ)と、集合を組み合わせて考えると、それまで知られていなかった、意外な事実が起きることを発見したのである。
前回も3という自然数を、要素が3個の集合の全体、つまり、要素が3個の集合の全部からなる集合として、定義した際に、3個という数が無くとも、二つの要素が有限しかない集合の個数を比べることができることを、運動会の玉入れの話を使って説明した。
つまり、こんな風にして、二つの篭の玉を同時に捨てて行けば、早く球が尽きた方が、玉の数が少ないことになる。
そして、もし、同時に玉が尽きれば、玉の数は同数ということになる。
普通は数を数えながら玉を捨てるが、数を数えなくても、判定はできる。
つまり、数の概念を知らなくても、数の大小と、同数の判定ができることになる。
カントールは、これと同じ方法で、集合の要素の数を比較した。
つまり、二つの集合A,Bの要素が同じであることを、その集合の要素の間に「一対一対応」があることとして定義した。
AとBの間の一対一対応とは、AからBへの関数(写像) f で、
という2条件を満たすものをいう。一対一対応の逆関数は、BとAの一対一対応になる。
有限集合の場合には、一対一の対応が数を数えることの代用となるのは直観的にわかる。
これだけでは何も、面白くはないのだが、。集合が無限に要素を持つときに、これをやると様子が変わる。
たとえば、AとBとが同じ数だけ要素を持つとき、Bに一つ新しい要素を追加すれば、当然、Bの要素はAより一つ多いので、AとBの一対一対応は作れなくなる。
しかし、AやBが無限集合だとこれができる。
たとえば、A1を{1,2,3,…}という集合としよう。当然ながら、AとAとの間には、f(a)=a という一対一対応がある。
しかし、このA1に0を追加してB1={0、1,2,3,…}を作っても、f(a)=a-1 とすると、一対一対応になってしまう。
A1はB1の真部分集合になっている。つまり、無限に要素をもつ無限集合では、真部分集合との一対一対応が出来てしまうのである。
無限集合を数えることは無理でも、この様に、無限集合の間の一対一対応は考えることができる。 そこで、カントールは、無限の個数を、一対一対応の概念を使って定義した。
AとBとの間に一対一対応があれば、AとBは同数。AとCが同数の、Bの部分集合Cがあれば、Bの要素の個数はAの要素の個数以上であり、さらに、AとBの要素の個数が同数でなければ、つまり、一対一対応が存在しなければ、BはAより、本当に大きな数の要素を持つと、カントールは定義したのである。
カントールは、この様に無限集合にまで拡張された、集合の要素の「個数」を濃度と呼んだ。 一対一に対応づけられる二つの集合は同じ濃度を持つと考える。 また、Aより本当に大きな数の要素を持つBの濃度は、Aの濃度より大きいと考えるのである。
先に示したB1とA1で言えば、B1の濃度は、その真部分集合A1の濃度と一致するのである。
先に、自然数3を、要素が三つの集合の全体として定義した。この3という概念は、濃度という言葉を借りれば、別のやり方で定義することができる。
まず、何でも良いので、三つのもの。例えば、空集合 ∅、空集合の集合 {∅}、そのまた集合{{∅}}という三つのものを持ってきて、その三つからなる集合 {∅,{∅},{{∅}}} をつくり、「{∅,{∅},{{∅}}}と濃度が一致する集合の全体」を3と定義することができる。
そうすると、{0,1,2,…}という自然数の全体の集合と濃度が一致する集合の全体、というものも作ることができる。カントルは、これをℵ0(アレフゼロ)と名付けた。
同様に、実数の濃度と濃度が一致する集合の全体なども考えることができる。
カントルは、同様に、ある集合と濃度が一致する集合全体をℵ(アレフ)と呼んで、自然数の無限版だと見なした。
カントルは、この様な濃度や超限基数の概念を使って、次々に無限集合の不思議な性質を発見していった。
たとえば、実数全体の集合Rの濃度と、平面上の点の集合、つまり、二つの実数の対(x,y)の集合R×Rの濃度は同一である。カントルはこれを証明したとき、デーデキントに、「私は、この事実を見ることが出来たが、それを信じることができない」という意味の手紙を書き送っている。要するに一次元の数直線と、平面の点の数が同じだというのである。確かに、なかなか納得が出来ない事実である。
カントルが、集合論のための集合論を開拓していった切っ掛けは、この数直線と平面の濃度の不思議な関係を発見したことだと言われている。
カントルは、この他にも数々の濃度についての新事実を発見していったが、その中に、「自然数の全体の濃度は、実数の全体の濃度より小さい」という定理がある。
カントルは、これの二つの証明を出版しているが、その第二の証明に使われたのが、「対角線論法」という有名な方法だった。
そして、カントルは、この方法を使って、さらに、「どの様な集合でも、それよりさらに濃度が大きな集合がある」という定理を証明した。
つまり、濃度には限界がないのである。
そして、この発見が、その後の、数学の基礎を大きく揺るがせることとなった。
その「どの様な集合でも、それよりさらに濃度が大きな集合がある」という定理は、次のように証明された。
集合Aに対して、その部分集合の全体の集合{X|X⊆A}を考える。この集合は、冪集合と呼ばれて Pow(A)とか、2^A と書かれる。(参考)
カントルは、このPow(A)の濃度が、必ずAの濃度より大きいことを証明した。
AからPow(A)の関数として、a∈Aとなる aに、{a}を対応させる関数 f(a)={a}が考えれられる。
これに対して、Pow(A)には、たとえば、f(a)という形で表すことができない、空集合が含まれている。
しかし、それだけでは、Pow(A) の濃度が、Aの濃度以上であることがわかるだけで、本当に大きいということはわからない。
その「本当に大きい」ということを示すために、カントルは、AとPow(A)の間に一対一対応 f があると仮定して、
D={x∈A|x∈f(x)とならない}
という集合Dを考えた。
明らかに、D∈Pow(A) であるが、この定義から、f(a0)=D となる a0 は存在できないということが証明できるのである。
これの証明と、何故、これを「対角線」論法というのかということは省略するが、興味がある人は、例えば、こちらを見て欲しい。
どんな、集合Aでも、その冪集合 Pow(A) は、その濃度が大きい。
では、「すべての集合の集合」は、どうだろうか。これをALLSETと書くと、
明らかにPow(ALLSET)⊆ALLSETである。
これから、Pow(ALLSET)の濃度は、ALLSETの濃度以下なる筈であった。
しかし、カントルの定理は、Pow(ALLSET)の濃度は、ALLSETの濃度より大きいということを示していた。
これは明らかに矛盾である。
カントルは、この明らかな矛盾を、集合論の深遠さを示す事実と解釈した。
しかし、すべての人が、そう考えたのではない。
例えば、この講義の最初の方に出て来た、哲学者ラッセルがそうである。
講義の最初の頃に引用した、哲学者、B.ラッセルは、20世紀の最初のころ、デーデキント的な、集合をつかって数学を再構築するというプロジェクトを実行していた。
デーデキントやカントルは、集合という概念を使っていたが、それについて議論する際には、ドイツ語のような「自然言語」を使っていた。
これに反して、ラッセルは、自然言語の代わりに、記号論理学とか数理論理学と呼ばれるものを使った。
ワイエルシュトラスの方法、つまり、イプシロン・デルタ論法で収束を定義する方法の説明の所で、
![]()
の定義である、

を、「論理の部分」である
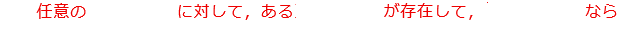
と「数の部分」である

に分けた。
この説明で、「論理の部分」と呼んだ部分が自然言語の部分である。要するに、論理の部分、自然言語の部分とは、「言葉」の部分である。
詳しい説明は、後の講義に譲ることになるが、ラッセルは、この「言葉」の部分も、記号論理学と呼ばれる、数の部分で使われる数式のようなものに置き換えた。
ラッセルは、この数理論理学により、ワイエルシュトラスの収束の定義を、一切、自然言語を使わずに、すべて数式のようなもので書くことができたのである。
同様の工夫により、ラッセルは、例えばカントルのパラドックスの様な議論を、
の二つだけからなる論理式と呼ばれるもので、記述することに成功した。
クロネッカーの一般算術においては、-1を、u1+1=0 という「公理」を伴う不定元 u1 とすると、-1*-1=1 となることを、
(u1+1)*(u1+1)=u1*u1+2u1+1
(u1+1)*(u1+1)=0*(u1+1)=0
u1*u1+2u1+1=0
2u1+1=u1+(u1+1)=u1+0=u1より
0=u1*u1+2u1+1=u1*u1+u1
0=u1*u1+u1
両辺に1を足して
1=1+0=u1*u1+u1+1=u1*u1+0=u1*u1
という計算だけで示すことができるということを説明したが、ラッセルは、イギリスの数学者ジョージ・ブールの研究を発端として、19世紀に発展した記号論理学というものを使い、同様の「式の計算」のようなもので、それまでは自然言語で書かれていた、数学の証明を、数式の計算のようなもので置き換えることに成功したのである。
デーデキントが、ドイツ語を使って、実数や自然数を集合に還元し、ワイエルシュトラスが、ドイツ語を使って収束の概念を実数の数式に還元したように、ラッセルは、記号論理学を使って、すべての数学を集合についての数式に還元したのである。(ワイエルシュトラスの収束の定義の「数の部分」には、「正の実数ε」という自然言語があるが、これは「ε>0」という数式に置き換えることができる。)
ラッセルは、カントルのパラドックスは、ドイツ語という自然言語を使ったために起きた、何らかの誤解に起因するものだと考えた。そして、自然言語を記号論理学という、数式のような言葉に置き換えれば、どこで「計算間違い」をしたのかが分かって、パラドックスは解消されるはずだと考えた。
しかし、実際に、それをやってみると、見つかったのは、非常に単純な、言い訳のできない集合というものが本質的に持つと思われるパラドックスだった。これをラッセルのパラドックスという。
ラッセルのパラドックスは、カントルの対角線論法による集合Dの定義
D={x∈A|x∈f(x)とならない}
の f を一番簡単な場合、つまり、f(x)=x として、Aを集合全体の集合にすることにより得られる。
まだ、記号論理学の説明をしてないので、記号論理学の部分を日本語で書いて、このパラドックスを説明し様。
まず、
R={x|x∈Set かつ x∈xとならない }
という集合を考える.ただし、Set は集合全部の集合である。
そうすると,実は
R∈R とならない ⇔ R∈R
となり,これは矛盾となる.
何故か?
R∈Rならば,Rの定義{x|x∈Set かつ x∈xとならない }から,「x∈Set かつ x∈xとならない」 の x に R を代入したものが正しいはずである.
つまり,
R∈Set かつ R∈Rとならない
だから,R∈Rとならない、である.
逆に,この「R∈Rとならない」を仮定すると,Set(R) だから,
Set(R) かつ R∈Rとならない
となる.これは R の定義,{x|x∈Set かつ x∈xとならない }に合致するので,
R∈R
のはずである.
もし,R∈R が正しければ,R∈Rとならない、となって矛盾.
もし,「R∈R とならない」 が正しければ,R∈Rとなって矛盾.
つまり,R∈R は真でも矛盾,偽でも矛盾.
つまりは,ラッセルの論理学から生み出した数学は,矛盾している!
これをラッセルのパラドックスという.
これが記号の為に分からない人は,次のように考えればよい.
本のカタログは,本の情報の集合体(集合)だと見なせる.
ある出版社が,カタログにそれ自身が掲載されていないようなカタログだけを集めたカタログRを作ることにした.
このカタログR自身の情報は,このカタログRに掲載すべきか?
もし,そのカタログRにR自身が掲載されていたら,「カタログにそれ自身が掲載されていないようなカタログだけを集めたカタログ」という条件に反する.
だから,カタログRにR自身の情報は掲載してはいけない.
だから掲載しないことにすると,Rは「カタログにそれ自身が掲載されていないようなカタログ」になってしまうので,編集方針からしてRを掲載しないといけない.
これは,嘘つきのパラドックスと呼ばれるものと類似したものである.この嘘つきのパラドックスとは,
あるカードに次のように書いてあった.このカードに書いてあることは嘘か本当か?

まるで冗談のような話であるが、ラッセルのパラドックスは、集合を使って数学を行っていたデーデキントなどの人たちに大きな衝撃を与えた。
クロネッカーなどの根強い反対があったものの、20世紀のはじめころには、とくに若い数学者を中心にして、デーデキントやカントルの集合論を使って数学を行うことは、常識となっていっていたのである。
その最中に、ラッセルのパラドックスが発見された。
このため、数学者の多くは、これを「数学の危機」と考えた。
特に、この問題を深刻にとらえたのが、20世紀数学を作ったひとと言われることもある、ドイツの数学者ダービット・ヒルベルトであった。
彼は、この問題を解決すべく、数学基礎論とか、超数学と呼ばれる、数学の新しい分野を開拓した。
次に、このヒルベルトの数学基礎論の話にうつる。