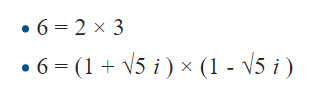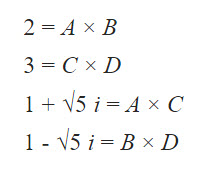全学共通科目「科学史」メモ 2016.11.24
前回までに話して来たこと 中間のまとめ
なぜ、集合論の様なものが、数学で必要となったか、それは、ラッセルの The Principles of Mathematics のChapter 1, section 3 の次の議論が示している:。
The Philosophy of Mathematics has been hitherto as controversial, obscure
and unprogressive as the other branches of philosophy. Although it was
generally agreed that mathematics is in some sense true, philosophers disputed
as to what mathematical propositions really meant: although something was
true, no two people were agreed as to what it was that was true, and if
something was known no one knew what it was that was known. So long, however,
as this was doubtful, it could hardly be said that any certain and exact
knowledge was to be obtained in mathematics. We find, accordingly, that
idealists have tended more and more to regard all mathematics as dealing
with mere appearance, while empiricists have held everything mathematical
to be approximation to some exact truth about which they had nothing to
tell us. This state of things, it must be confessed, was thoroughly unsatisfactory.
Philosophy asks of Mathematics: What does it mean? Mathematics in the past
was unable to answer, and Philosophy answered by introducing the totally irrelevant notion
of mind. But now Mathematics is able to answer, so far at least as to reduce the
whole of its propositions to certain fundamental notions of logic. At this point, the discussion must be resumed by Philosophy. I shall endeavour
to indicate what are the fundamental notions involved, to prove at length
that no others occur in mathematics, and to point out briefly the philosophical
difficulties involved in the analysis of these notions. A complete treatment
of these difficulties would involve a treatise on Logic, which will not
be found in the following pages.
凡その意味:数学の哲学は、論争の的であり、曖昧で、数学の哲学以外の哲学の分野同様に、進歩が無いものだった。数学は、何らかの意味で真理であるということについては合意されていたと言えるものの、哲学者は数学の命題が一体何を言いしているのかということについて、合意にいたることはなかった。観念論者(idealist)は、数学は単なる形式を扱うものだと言い、経験論者は、数学は、真理への近似だと言う。哲学は数学に、数学は一体何を意味しているのだと問いかけたものの、数学はそれに答えることができなかった。しかし、今や、数学は、こういう哲学の問いかけに、数学の命題を、ある一定の論理学の基本的概念に還元することにより、答えることができるようになったのである。
そして、この哲学からの問いかけに、数学が答えることができなったものの代表として、次の三つを紹介した。
- 解析学の無限小
- リーマン面
- クンマーの理想数
解析学の無限小は、実際に、George Berkley バークリー僧正というアイルランドの著名な哲学者の1734年の著書 The Analyst で、厳密な哲学的理性から逸脱した数学者たちの間違えた理論として攻撃された。しかし、それに数学者たちは、まともに答えることはできなかった。それが、コーシーの理論を通して、ワイエルシュトラスにより完全に論理的に整合な説明がつくようになるまで、後120年ほどを必要とした。
また、この「哲学者をも納得させる基礎の欠如」は、単に哲学だけの問題ではなく、数学者が、数学的問題を解けない原因でもあった。たとえば、「連続関数は、例外点を除き微分可能」という命題が正しいか否かは、ワイエルシュトラスの解析学の基礎が誕生するまでは、決着をつけることができなかった。
そのワイエルシュトラス(1815-1897)の同時代人で、関数論という数学の分野の開拓で、ワイエルシュトラスのライバルでもあった、ベルンハルト・リーマン(1826-1866)が、その関数論のために導入したリーマン面という概念は、空想の産物でしかなかったが、大変に役に立った。一方で、ワイエルシュトラスは、同じ理論を無限級数を使って基礎づけたが、厳密である反面、リーマンが行ったような幾何学的な直観的議論ができず、面倒な計算が必要だった。
ちなみに、この関数論の最初の重要な一歩を踏み出したのはコーシーだった。また、リーマン面が、バークリーのような哲学者からの非難を浴びたという記録は、少なくとも林は知らない。ただし、リーマン自身は、哲学者ヘルバルトの影響をうけており、自分を自然哲学者だとみなしていたことが、彼の遺稿の研究により知られている。
そして、最期の例が、クンマーという数学者の「理想数」という概念。解析学における無限小やリーマン面と異なり、クンマーの理想数の理論は、難解ではあるものの、完全に理性的・論理的で、哲学者から非難を受けるような点はなかったともいえる。しかし、問題点は、彼が「理想数」というものについて語りながら、それが何かを全く説明しなかったことにあった。
クンマーは、ある数の「理想素因数」、つまり、「素因数となる理想数」の個数や、それが具体的に与えられた数を割り切るかどうかの条件を、疑い様のない明晰な数式で説明したが、しかし、「理想数とは何か」は全く説明しなかった。つまり、王様の服があるかのように完全な大意振る舞いをする数学的方法はしめしたものの、肝心の服は、まったく見えなかった。そして、そのことが、彼の理論を非常に難解で理解し難いものにした。
前回までの資料から
揺らぐ数学の基礎 クンマーの理想数の場合
ドイツの数学者エルンスト・クンマーは、フェルマーの定理に関連する整数論の研究研究において、理想数という概念を導入した。
その理論では、ラッセルが、Philosophy asks of Mathematics: What does it mean? Mathematics
in the past was unable to answer 哲学は数学に、数学は一体何を意味しているのだと問いかけたものの、数学はそれに答えることができなかった、と書いたような状況、つまり、理想数といかなる存在か、という問題が一切議論されないままで、それにも関わらず、理想数に関する非常に高度の数学的計算や証明が行われた。
これは、クンマーが、「理想数とは如何なる存在か」という問題を解決できなかったというより、意識的に、そういう哲学的問題を避けた可能性が高いらしい。
では、クンマーは、どうやって「どういう存在かわからない存在」について議論したかというと、それは「裸の王様方式」。
まず、このYouTube のアニメを見よう。これの6m56s から見る。
詐欺師や人々の言葉や手つきに注目:縫う、雲の手の上で王に差しだす、*語る*、着る(シーンは無い)、眺める、褒める、見えないけど納得する、裾を持ち上げる、…
*語る*で語られたこと(城の建物をでるまで、価値についての判断は除く):
- こちらは服とズボン、こちらはマント
- 蜘蛛の糸の様に軽い
- まるで着ていないよう
- よい出来だ
- 色も模様立派
- 体にピッタリ(似合っている)
- マントの裾を引きずっている
クンマーの理想数は、まさにこんな感じで導入された(これは悪口ではない!)。
理想数の解説をいくつか: 1 2 3(イデアルの歴史の説明)
上の3の例に基づく歴史的文脈を無視した説明:
クンマーというドイツの数学者が、「算術の基本定理」と呼ばれる、素因数分解の一意性の定理を、普通の整数以外の「整数もどき」に拡張しようとした。これができれば、有名なフェルマーの定理が証明できるはずだった。素因数への分解は問題なかったが、それが一通りというのが難しかった。
クンマーが考えた「整数もどき」は、現在代数的整数とよばれているものの一種で、実体は、特殊な性質を持つ複素数(数Ⅱ)。
クンマーなどの数学者は、代数的整数の部分集合で、上の解説の3で使っているRのように、整数の全体と似た性質をもつものを考えた。
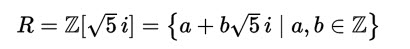
この R のどういう点が、整数(の全体)Zに似ているかというと、四則演算で「閉じている」様子が似ている。
a, b ∈Zならば、つまり、a, b が整数ならば、四則演算の加減乗除の、加減乗、つまり、足し算 a+b、引き算a-b 、掛け算a*b の結果は、やはり、整数。これを、Zは足し算、引き算、掛け算で「閉じている」という。明らかに、このRも、足し算、引き算、掛け算で閉じている。
また、Zは、a=1, b=2 の割り算の結果1/2が整数でないので、割り算については閉じていない。また、Rの場合には、a=1, b=√5iの場合、a/b
は、(-1/5)
√5i となって、-1/5 が整数でない(Zの要素でない)ので、R の要素にならない。つまり、やはり、割り算で閉じていない。
このRの場合、3の説明にあるように、6は、次の二つのように素因数分解できる。
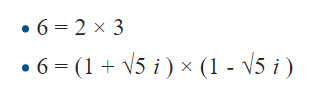
2、3、1+√5i, 1-√5i は、全部、Rの「素数」つまり、これは1と-1以外では割り切れない。
ということは、素因数分解が二通りあることになる。
そこでクンマーは、「理想数」という仮想的な数を導入して、これらの4つ数がさらに理想数で割り算できる、さらには、その理想数の範囲の素因数分解はひとつしかないと考えた。
つまり、3の説明にある
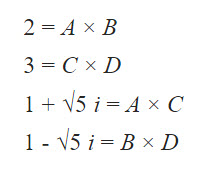
という状況である。(A,B,C,Dが理想数の素数。)
クンマーは、このA,B,C,Dのようなものが「あったとしたら」、その計算結果がどうなるかというようなことを完全に説明できる理論を作った。
しかし、その肝心のA,B,C,Dの「実体は何か」ということは、決して、説明しなかった。
つまり、クンマーは、ないもの(理想数)を、あたかも存在するかのように語った。
ないものをあるかのように語る!
それはラッセルが批判したことそのもの。
哲学者は納得しない。数学者でも困惑するひとがいる。
リーマン面とよく似た状態だが、リーマン面の方は、まだ、紙のモデルで「実体?」を説明できた。
つまり、幾何学的直観が伴っていて、現実(この3次元空間)を、想像力ですこし「拡張」すれば、イメージできないこともなかった。
- これが容易にイメージできた人は、数学の才能がある可能性が高い。
- ちなみに、若いころの林は、これをイメージするのに苦しんだ。実際、林は数学者には、あまり向いてない。
こちらは、「蜘蛛の糸の様に軽い」というような性質だけはわかるのだが、「形」、「存在」が、全く確認できない、「見えない服」のようなものだった。
これでは、ラッセルの様な哲学的疑問に答えられない。では、どうする?
これにはデーデキントという数学者とクロネッカーという数学者による、二つの異なる解決法があった。
そのどちらもが、ある意味では、「裸の王様」の「見えない衣装」と同じ考え方に基づいていて、それは現代でいえば、ポケモンGOなどにも使われている、AR 拡張現実という手法に似たものだった。
そこで、まず、拡張現実の話。
仮想現実と拡張現実
仮想現実というものを知っている人も多いと思う。
たとえば、3Dグラスの Oculus。これをかけて、3D画像を見ると、人間はこんなになる。
さらにアドバンスドになると、歩行の様子まで仮想で再現する技術さえできている。こんな風とか、こんな風。
最初の方の動画は、ジェットコースターなどの現実の存在の画像を再現している。
画像を見ている人は、その場にはいないのだが、3Dで立体的に画像が動くと、つい体が動いてしまう。
つまり、ほぼ完ぺきに、実体が生み出す画像という刺激が、再現されると、我々は、現実には乗っていないのにジェットコースターに乗っているかのように錯覚する。
そして、後の方の、歩行による移動までバーチャルに再現する方は、画像がアニメであったように、実は実体がない。人工的に「現実」が作り出されている。
しかし、その人工の現実の中を「歩く」女性は、本当に歩いているように感じ、また怖がっていた。
こういうのが仮想現実。仮想現実には、実体があり、その画像が記録されたものが再現されているものと、「実体」さえもが人工的に作り出されたもの、この二つがあることに注意。
現実が記録されたもの、と書いたが、もちろん、それは、今、その場で撮影されている画像でも構わない。つまり、リアルタイムで見ている画像でもよい。
たとえば、3Dグラスにより、ドローンに搭乗して、操縦することさえできるようになっている。
あるいは、リアルタイムで撮影されている画像に、作り出された現実が重ね合わされていてもよい。
たとえば、ポケモンGOの画面は、そうなっている。
自分でやったことがない人には分かりにくいかもしれないので、ソニーの拡張現実 SmartAR。
つまり、これらは、現実の画像と、人工の画像のハイブリッド。
いってみれば、存在するものと、存在しないもののハイブリッド。
それなのに、我々は、あたかもポケモンがいるかのように行動する。
こういうのを、現実が、仮想の現実(存在しないもの)で拡張されたもの、拡張現実という。
ある意味で、それは「裸の王様」で起きていたことと同じである。
そのことを頭において、「裸の王様」のアニメと、先ほどのホラーゲームの世界に入り込んだ女性の姿を比べてみて欲しい。
また、有名なパフォーマー「カゲム」のこの画像と比べてみて欲しい。
現実と、非現実が、完全にシンクロすると、こういう風に、存在しないものが、存在しているかのようにみえる。
クンマーは、
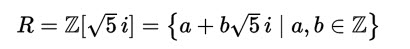
という「現実」に、理想数という拡張現実をつけ加えたといえる。
しかし、クンマーは、どうやって拡張現実をつくりあげるかは示さなかった。
クンマーが行ったことは、「裸の王様」のように、みんなが「ないものをあるかのように行動したら、あるような気分になるよ」ということまで。
それに対して、デーデキントとクロネッカーが行ったのは、丁度、ポケモンGOやソニーの SmartAR のように「拡張された現実(理想数)が画面に見える」ようにしたこと。
実は、抽象的で難しいことのようにみえるが、デーデキントやクロネッカーがおこなったのは、この「拡張現実」と同じことである。
そして、現在の拡張現実に3Dグラスを使う方法、スマホを使う方法(ポケモンGO),、プロジェクションマッピングを使う方法(カゲム)、のように、色々なやり方があるように、この二人のやり方は、少し違っていた。
デーデキントは、集合という技術を使い、クロネッカーは、代数計算とい技術を使った。
次の、この話をする。まずは、簡単なケースには、非常に簡単な、クロネッカーの方法の方から。
ここから今回の資料
クロネッカーの一般算術と数学の算術化
クンマーの理想数の理論を構築するために、理想数に対して知るべき性質は、たとえば、上で記号A,B,C,Dと書いた仮想的な存在である四つの理想数のそれぞれが、具体的に与えられた数(代数的整数)αを割り切る条件であった。
このA,B,C,Dは、その「実体」が何かが知られていなくても、
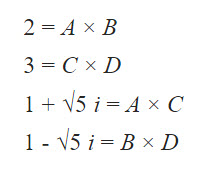
を利用して、
- 2と1+√5i を割り切るA
- 2と1-√5i を割り切るB
- 3と1+√5i を割り切るC
- 3と1-√5i を割り切るD
の様に、「名指し」することができる。つまり、Aとは、「2と1+√5i を割り切る理想素因数」である。
そこでクンマーは、「Aがαを割り切るための条件」を、2と1+√5i とαから作られる数式を利用して定義したのである。
これにより、クンマーは「Aの実体」に一切触れることなく、Aについての数学理論を展開することができた。
ポケモンGOという拡張現実の中のポケットモンスターは、単なるアニメであって、それに実体、たとえば、心臓や脳などの内臓があるわけではない。
しかし、それがどの様な場所に現れるか、どの様に我々を見るか、モンスターボールを投げつけて捕獲するときの捕獲難易度などが、予めアルゴリズムで決まっていて、そのアルゴリズムが、プレイヤーの現実の位置や向きや移動速度(これらはGPSのデータ)、モンスターボールの投げつけ方(実際には、タッチスクリーン上の指の動き方)を入力として計算することにより、ポケモンが投げつけたモンスターボールの中に捕獲されるか、あるいは、一旦捕獲されても逃げてしまうかなどが決まる。
つまり、上の理想数の場合の「Aがαを割り切るための条件」を「2と1+√5i とαから作られる数式」で定義したのと同じように、「ポケモンを捕まえられるかどうか」を、プレイヤーの現実の位置や向きや移動速度(これらはGPSのデータ)、モンスターボールの投げつけ方(実際には、タッチスクリーン上の指の動き方)を入力として計算している。
この赤字の部分と青字の部分対応をみれば、実はクンマーの方法は一種の拡張現実だったことがわかる。
ただ、ポケモンGOの場合には、「実体」は存在しないポケモンが、ハッキリと直感的にわかるアニメで表されているのに比べて、クンマーの場合には、そういう直感的なものがなかったので、非常に分かり辛かった。さらにいえば、こういう「実体がないけれども、みんなである振りをすることにより、あたかも存在するかのようにしてしまう、という方法の一般的なやり方をクンマーは示さなかった。それも彼の理論を分かり辛くした。
これに対して、クンマーのギムナジウム時代以来の弟子だったクロネッカーは、一般算術という理論で、この「実体がないものをある振りをして現実にしてしまう方法の一般論」を作り上げた。
そのアイデアの基本は、実にあっけないほど簡単で、たとえば、整数の全体をZとして、変数を無限個考え u1, u2, u3,..... これを変数としてもつ多変数の多項式の全体
Z[u1,u2,u3,....]を考えて、それを拡張現実の全世界だと考えるというものだった。その世界では、u1, u2, u3,.....が、たとえば、ピカチュウなどの仮想的存在の役割を果たす。(実際には、Zでなく自然数で始めたり、有理数で始めたりする。)
ただし、この一般代数で、クロネッカーがクンマーの理論を拡張したやり方は、たとえば、先の A, B, C, D として、 u1, u2, u3,.....
の幾つかを使うというような簡単な話ではなかった。クロネッカーは、クンマーの理論を完全に書き直し、たとえば、クンマーでは、それが最重要だった、理想素因数という概念も、理論の中心からは外されていた。そのため、理想数による素因数分解という、もともとの問題を例にすると、その雰囲気でさえ、ここで再現するのは難しい。
そこで、クロネッカーの一般算術の一番易しい場合を幾つか紹介して、クロネッカーの「拡張現実」の方法の雰囲気を説明する。このクロネッカーの方法は、後で説明するデーデキントのイデアル論に圧倒されて、そのままの形では、後世に大きな影響を与えることがなかったが、数学科の代数学などで教えられる代数拡大というものが、このクロネッカーの理論のシンプルな場合である。また、クロネッカーが目指そうとした理想は、後に、アンドレ・ヴェイユというフランスの数学者の「整数論と代数幾何学の融合」という構想を受けて、アレクサンドル・グロタンディークと、その仲間たちにより、半ば達成された。そして、このヴェイユやグロタンディークの理論は、20世紀数学の最高峰のひとつとみなされている。
簡単なケースで解説
この様に、クロネッカー流のアプローチは、先に進むと、その実行が大変難しくなるが、シンプルなケースでのクロネッカーのアプローチである一般算術は簡単。
クロネッカー版の「理想数理論」である、一般算術を用いる「序数の理論」(divisor theory)は、大変むずかしいので、同じ精神と道具を使った簡単な数学存在の基礎づけのケースで、一般算術の精神と方法を解説する。
理想数の話をするときに、1+√5iや1-√5iのような数を考えたが、良く考えてみると、これらの数自体が、大体、理想数並に不思議な存在。
何が不思議かと言えば、まずは、虚数単位 i 。虚数というのは、imaginary な数、つまり、実際は存在しない数、想像上の数という名前なのだから、随分、不思議な存在。
また、√5などというものも、考えれば中々良くわからない存在である。これは有理数ではなく、無理数となる。
無理数は、英語では、irrational number、つまり、不合理な数、つまり、「無理をした数」、「理屈の通らぬ数」なのである。
さらに言えば、負の数などというのも、良くわからないものである。実は、負の数とは何ぞや、それは存在するか否かというのは、結構議論の的になっていた。
たとえば、高校でも学習する、ドモルガンの法則の de Morgan は、負の数を合理化しようとして苦労したことが知られている。
これは19世紀のことだが、ドモルガンの岳父で牧師で社会改革家として知られた Wiliiam Frend は、非常に頭脳明晰な人だったが、それ故に「負の量」というものを認めなかった。それを何とか納得させようと、ドモルガンは奮闘したといわれている。つまり、負の数についても、19世紀になお、ラッセルが書いたような、哲学的質問に数学が答えられないという状況があった。
これらを一挙に実にあっけなく解決する方法が、クロネッカーの一般算術であった。その考え方は、ドイツの大数学者ガウスにまで遡るのだが、それは今回は置いておいて、考え方だけを説明する。
出発点は自然数
クロネッカーの出発点は、自然数である。
このことから、クロネッカーが「すべての数は人間が作ったものだが、自然数だけは神が作った」と言ったということが良く言われる。また、それがクロネッカーが数学の基礎に神学のようなものを置く古臭い数学者だったことの根拠の様に言われることがあるが、これは間違い。
クロネッカーは、自然数も人間が作ったと思っていた。彼は19世紀的な合理主義者で、神など信じてはいなかったのではないかと思われる。少なくとも、数学の話に神を持ち込む意図は全くなく、数学も哲学科で教えられていたような時代に、哲学さえも数学から排除しようとした。そのことは、後で説明することにして、取りあえずは、自然数から始める。
その自然数は、0から始まるとして、0,1,2…のことである。その全体(の集合)をNと書くことにする。
一般算術
係数が自然数の変数 u1 の多項式の全体を考え、それを N[u1]と書くことにする。たとえば、u1+1 とか u1^2+3*u1+1 などがその例である。まだ、負の数は考えないので、引き算は一般にはつかえない。掛け算と足し算だけ使えるとする。また、u1^2
は、u1 の二乗を示している。
そして、u1+1=0 という「方程式」を導入して、それを公理の様に使うことする(数学の用語では、 u1+1 を法とするという)。
ここで公理の様に使うという意味は、u1+1 という式があったら、それを0で置き換えてよいし、逆に、0はu1+1 に置き換えてよいという意味である。つまり、式計算の際に、u1+1=0を使ってよいということである。そういう約束事にするということである。
ただし、ここで重要な約束事をする。u1 は便宜的に「変数」と呼んだが、実は、これは「不定元」と呼ばれるもので、変数と違い、代入してはいけないことになっている。もし、これに代入してよいとすると、u1+1=0 の u1に0を代入して、0+1=0、よって、1=0になってしまって数学が矛盾してしまう。
そのため、これは一種のシンボル、あるいは、定数の様に扱う。これが、クロネッカーのポケモンである。
つまり、u1 を不定元として、u1+1=0 を式の計算に使って良いということは、「何か分からないが u1 というものがあって、それに1を足すとゼロになる」ということを言っている。つまり、u1
という仮想現実が、現実の数のシステムNに追加されたことになる。
この様な代数的体系を、N[u1]/(mod u1+1) と書くことにする。この体系は、要するに、自然数が係数の u1 の「多項式」(クロネッカーは形式
Form と呼んだ)に通常の代数の式の計算の規則に、u1+1=0 という計算規則を追加したものに過ぎない。しかし、これにより、u1 は、完全に
-1 の役割を果たす。
たとえば、-1*-1=1 は、
(u1+1)*(u1+1)=u1*u1+2u1+1
(u1+1)*(u1+1)=0*(u1+1)=0
u1*u1+2u1+1=0
2u1+1=u1+(u1+1)=u1+0=u1より
0=u1*u1+2u1+1=u1*u1+u1
0=u1*u1+u1
両辺に1を足して
1=1+0=u1*u1+u1+1=u1*u1+0=u1*u1
という引き算を使わない、中学校レベルの式計算だけで示すことができる。
つまり、哲学者ラッセルが、「負の数-1とは何か、負の数-1の二乗が1だというのはどういう意味なのか」と聞いて来たら、これを示すことにより、その質問に完全に答えることができる。
ただし、ラッセルが、-1を u1 とみなすということに納得するかどうかは別の話。クロネッカーは、「私の-1とは、このことだ」と答えることができるということ。しかし、実用上は、これで完璧。
クロネッカーの方法では、a-b という演算は、a+u1*b のことだとして、a-a=0 などの法則が同様に計算できた。
要するに、こうやって「負の数」と引き算が導入できた。
これと同じく、√5は、u2^2=5 という式を「公理」とするだけで、u2 が√5の役割を果たす。
また、虚数単位 i でさえ、u3^2=-1、つまり、u3^2=u1 を「公理」とすれば、u3 を虚数単位にできることがわかる。
さらに言えば、分数 2/3 なども、u4*3=2 を「公理」とする、u4 だと思えば良い。
クロネッカーの方法では、この様に簡単に、様々な「仮想現実的な数」を、導入することができた。
凄く簡単に見えるが、実は、多変数の多項式は、割り算のアルゴリズムさえが一変数の多項式の場合のように簡単にはいかず、実際の数学理論を建設にすることは、非常に難しく、この様なやり方で、クンマーの理論を再構築することは容易なことではなかった。
しかし、クロネッカーの方法では、中学や高校で習う様な、式の計算だけで、すべてが説明されるという、良い点があった。
当時のドイツでは、数学とは式の計算の学問であるという見方があり、式計算は、哲学を必要としないものと見なされていた。
つまり、ラッセルがいう、「哲学的な問題」が、すべて式計算という現実的なものに還元できたのである。
また、クンマーの理想数にあたる、「序数」 divisor も、やはり、一般算術の Form を使って定義された。ただし、先に述べたように、理想素数
A,B,C,D に対応する、不定元を導入するというような話ではなくて、理想素数は、殆ど使われない理論だった。ただし、クンマーの理想数にあたるものは、一般算術の
Form として明瞭に定義されており、それらを、すくなくとも原理的には数式として実際に計算して作り出すことができた。現在で言えば、コンピュータで計算できるようなものだった。
クロネッカーは、この様な方法で、無限小解析にようなものを行う構想させ持っていたらしい。たとえば、u5^2=0 とすると、二乗するとゼロになる無限小が、u5^3=0とすると、三乗するとゼロとなる無限小が導入できる。ただし、こういうものがちゃんと扱えるようになったのは、クロネッカーより遥か以後のことである。
では自然数は?:クロネッカーの真の姿
クロネッカーの一般算術の理論は、自然数だけは仮定していた。そうすると、自然数はどうするのかという問題が残る。これについて、クロネッカーが「自然数は神が作った」と言ったということが言われているが、これは実際に言ったのは確からしいが(後で解説)、クロネッカーが、そういう風に論文などに書いたものはない。
クロネッカーの遺稿は、実はドイツの第2次世界大戦の敗戦の余波で、失われてしまったことが知られている。戦火を避けて、廃坑に保存されていたものが、敗戦のために放置されることになり、やがて、その廃坑でガス爆発事故が起きて、完全に消失(焼失?)してしまったという。
しかし、クロネッカーが、彼の数学思想を講義した講義録Ueber den Zahlbegriff (数の概念について)が残されており、それによると、彼は、ジョン・スチュアート・ミルの数学論風の経験主義的な議論をしていて、まず、first, second のような ordinal number 序数が、並んだものに名前をつけるために発明され、それが、やがて、物の数を数えることと関係があることが認識されて、個数を数えるための数、 cardinal number 基数が発明され、それにより自然数の概念が成立し、さらに、その演算の体系、やがては、彼の一般算術の基礎を成す、式計算の数学が生まれた、と説明している。要するに19世紀的な合理主義の範囲で、神などに言及せずに、クロネッカーは人間中心的に数学を基礎づけた。
この講義録は、数学が天文学のような自然科学の基礎として重要であるだけでなく、それは現代を過去から分かつ、通商や交通の大発展の基礎でもある、という文章で締めくくられている。
クロネッカーはユダヤ人で、彼の一族は、農業や金融で大きなビジネスを行っていたらしいが、彼はベルリン大学を卒業したのち一度郷里に帰り、一族のビジネスを助け、その後の人生を働かずに暮らせるほどの莫大な蓄財をした。
そして、その後、ベルリンに帰り、大学で教えて収入を得る必要も無いので、自由人の学者として活躍し、社交界でも有名だったという。そして、「趣味」で数学を行い、大学で教える権利やベルリンアカデミーの会員の資格も得ている。そして、クンマーが亡くなって後、その空席を埋めるために、漸くベルリン大学教授となった。
また、最晩年に彼は、ユダヤ教を捨てて、キリスト教に改宗している。おそらくは、少し前に亡くなった夫人と同じ墓に葬られるためだったのだろう。(クロネッカーと、その婦人の墓は、その財力を反映してか、数学者のものとしては、特別に豪華。ちなみに、他の数学者の墓:ワイエルシュトラス、デーデキント)。
彼の行いには、神の様な超越的存在を信じず、人間の理性の可能性を信じる、19世紀のドイツ近代人の合理性が目立つ。
「集合論の創始者カントールを苛めた、守旧派の老数学者」という一般向け解説書によくある姿は見られないのである(九大の高瀬教授の数学史の論文の出だしを参照)。
むしろ、神学的だったのは、後で説明するように、そのカントールの方だった。
次は、そのカントールの「盟友」で、現在は、むしろカントール以上に、集合論の創始者としての地位が相応しいとされている、リヒャールト・デーデキントの「理想数理論」であるイデアル論の話。