全学共通科目「科学史」メモ　2016.10.27

質問票への回答のための資料

  1. 西田哲学で数学を基礎づけようとした人は？
  2. 数学と音楽

前回の資料から（少し改善してある）

参考文献

前回説明したように、この講義の内容は、今書いている新書を元にしており、新しい内容。しかし、もとになっている本は幾つかある。簡単に読めるものは少ないが、それらをリストしておく。

この他に、昨日みつけたのだが、数学セミナーという雑誌の2016年11月号[特集　リーマンが目指したもの]に、東工大の数学者加藤文元さんが書いている「リーマンと空間概念」が、林と同じ種本を元にしていて、数学のことを知っている人たちには、講義の理解の助けになるかもしれない。この人には数学史の新書などがあるので、今、注文中。

不完全性定理は人類の知の限界を示す？

不完全性定理とは、1931年1月、オーストリア共和国の首都ウィーンの学術誌「数学物理学月報」に発表された論文「プリンキピア・マテマティカおよび関連した体系の形式的に決定不能な命題についてⅠ」で発表された二つの定理。論文の著者はクルト・ゲーデルという二十四歳の青年数学者（ゲーデルの写真）。

この論文には、全部で十一個の定理があったが、その六番目の定理が、「第一不完全性定理」、十一番目が「第二不完全性定理」。そして、この二つをあわせて「不完全性定理」という。

第一不完全性定理は、イギリスの二人の哲学者兼数学者、ラッセルとホワイトヘッドによる数学書プリンキピア・マテマティカの数学体系や、それに関連する公理的集合論という数学体系（質問票への回答のZFは、その一例）には、それらの体系の証明方法では、肯定も否定も出来ないような問題が存在することを示していた。

プリンキピア・マテマティカや公理的集合論がどんなものか、後で説明するが、それはどちらも数理論理学という数学の分野の研究対象。つまり、これらを対象とする定理である不完全性定理は、数理論理学の定理であり、数学の定理である。

ところが、その数学の定理が「人類の知の限界を示している」と言う人がいる。そのひとりが、アメリカの原爆開発を率い、後に反核運動に転じた物理学者オッペンハイマー。

オッペンハイマーは、ゲーデルが勤務していた米国プリンストン高級研究所の所長だったので、ゲーデルの六〇歳を祝うシンポジウムの際、シンポジウムに寄せる言葉を書いているが、その中でゲーデルが「人類の知性一般における限界の役割を明らかにした」と書いた。 オッペンハイマーは物理学者だが、同様の意見は、哲学とか、現代思想などの文系の人が主張することが多い。

こういう、不完全性定理が人類の知の限界を示すという意見に反して、不完全性定理は人類の知の限界など示してはいないと主張する人もいる。実は、その代表者が、ゲーデルその人。

ゲーデルは、現代的な懐疑主義の正反対の思想、少なくとも数学に限れば人類の知には限界などないという、「ゲーデルのプラトニズム」と呼ばれる思想を提唱したことでも有名な人で、不完全性定理により人類の知の限界が示されたなどとは、全く思っていなかった。

しかも、ゲーデルは、彼の不完全性定理を元に、この考えに辿り着いた可能性が高い。このことは、後で説明する。

哲学への数学の応用としての不完全性定理

現代の科学についての常識からすれば、科学や数学が、人類の知の限界などという、哲学の問題のようなものに答を与えるというのはいかがわしく聞こえる。ゲーデルの様に、知の限界ではないと主張することさえ、哲学的過ぎて数学者がやることではないというのが、少なくとも現代的常識。

それ以前に、ある数学定理の示すことに賛成派（オッペンハイマー）と反対派（ゲーデル）がいるという事自体がいかがわしい。数学の定理というものは、証明されれば、何か見落としなどのミスがない限り、ずっと真理だというのが常識。哲学とか、歴史学とかならば、学説に賛成派、反対派があって、論争が起きて当然だが、数学ではそうでないというのが常識。

実は、たまに、証明が間違えているか、完全かどうかで論争が起きることがある。しかし、それは例外的。また、変な人は別として、不完全性定理の証明が間違えていると思っている人はいない。

それなのに、どうして、こういう哲学か何かのような状況が、不完全性定理では起きてしまうのか？

その答を解説するのが、この講義の大きな目的のひとつなのだが、答のヒントは、すでに、今までの説明の中にある。上で

　　　　　　　　第一不完全性定理は、イギリスの二人の哲学者兼数学者、ラッセルとホワイトヘッドによる数学書プリンキピア・マテマティカの数学体系や、
　　　　　　　　それに関連する公理的集合論という数学体系には、それらの体系の証明方法では、肯定も否定も出来ないような問題が存在することを示していた。

と書いた。赤字のところを見て欲しい。「哲学者兼数学者」となっている。これがポイント。このプリンキピア・マテマティカという三巻の本が完成したのが、およそ100年前、第一次世界大戦のころなのだが、そのころ数学と哲学、自然科学と哲学の距離は、今では想像できない位、近かった。この距離は、その後の歴史で大きくかわり、数学で言えば、不完全性定理により、最終的に、数学と哲学が切り離されてしまった。この古代ギリシャ以来と言って良い、大きな歴史的出来事の流れを見せようというのが、この講義の最大の意図。

プラトンの学園の門に「数学を知らざる者、この門をくぐるべからず」と書かれていたのは有名。数学と哲学は、古代より非常に近かった。それが変わったのだから、これは大変な文化史的出来事といえる。そして、その変化の最大の原動力は公理的集合論で、最後の契機が不完全性定理だったというのが、この講義の基本的主張。

現代的数理論理学の基礎は、ほぼ完成させたのは、プリンキピア・マテマティカのラッセルなのだが、ラッセルが、プリンキピア・マテマティカを書くことになった、そのもともとの動機は哲学だった。

ラッセルは、数学の基礎についての哲学的問題を解決する意図をもって、当時、数学ではなく、哲学の一分野だと思われていた、論理学を数学化し、その数学化した論理学だけを用いて、数学をゼロから作り直すという本を1903年に発表した。それが、The Principles of Mathematics：

https://archive.org/details/principlesofmath005807mbp
や
http://fair-use.org/bertrand-russell/the-principles-of-mathematics/

などで無料で読める。本も簡単に手に入る。

これが数学書であると同時に哲学書として意図されていたことは、その前書き（Preface）や Chapter 1, section 3 の議論からわかる。つまり、この本は、数学の対象である数とか、図形とか、空間とか、そういうものは一体何なのか、という哲学的問題に決着をつけるために書かれたのである。

簡単に言えば、この本は、もともとは哲学の一部分であった論理学を、数学的テクニックを使って、数学化して数理論理学というものにし、それにより、数学の対象である数などを「定義」できることを示し、それにより、数学的存在とは何か、という古くからの哲学の問題に決着をつけようとしたものなのである。

不完全性定理というものがゲーデルによって考えられた、背景の一つが、この本にある。

実は、ラッセルは、これで数学的存在とは何かという哲学の問題が片付いたと、一度、思ったのだが、その後、自分の論理学の理論に矛盾を発見してしまった。

それが、現在、ラッセル・パラドックスと言う名前で知られる。集合にまつわるパラドックス。

そして、このパラドックスの問題を解決することを意図して書かれた本が、不完全性定理の対象となったプリンキピア・マテマティカだった。

つまり、もともと不完全性定理が対象とするものは、哲学と数学の境界上に位置するラッセルの論理学・数学だったのであり、ある意味で、それは哲学に対する数学の応用だった。要するに最終目的は「数学の哲学」と言えたので、そのために、哲学で起きるような、反対派、肯定派に分かれての、終わりのない議論が起きてしまうのである。

しかし、正確に言うと、ここまでの話は、実際の歴史をかなり単純化してあり、実際の歴史では、数学に強い哲学者ラッセルでなく、哲学的意図を強く持った、当時、最大の数学者ダーヴィト・ヒルベルトこそが、不完全性定理の最大の源流となる。これは「ヒルベルト計画」という話で、今は、複雑過ぎて説明できないので、後で段々と説明していく。

ところで、以上の説明で、「論理学」ということを説明なしで使った。そして、「哲学の一部である論理学」ともいい、数学の一分野である「数理論理学」とも言った。また、哲学者で、数理論理学を作ったラッセルは、集合にまつるわるパラドックスを発見したとも書いた。

つまり、説明の中に、論理学、数理論理学、集合論という三つのものが錯綜しつつ現れてる。この説明では、それらが、どんなもので、また、どの様な関係にあるのか、全く分からない。実は、その歴史的関係が分かり始めたのは、比較的最近で、参考文献のJose Ferreiros　の本が出版されてからといえる。この本の初版は1999年。

この比較的最近、分かり始めた、論理学、数理論理学、集合論の歴史的関係が、この講義の文化史的な数学史観の背景となっているので、それを理解することが、この講義を理解する上で、非常に重要となる。

しかし、論理学も数理論理学も、普通は高校では教えないし、大学でもなかなか学ぶ機会がない。

そこで、高校でも教えられている集合の歴史の話から始めて、論理学、記号論理学や、これら三者の関係を説明していく。

集合論の歴史１　揺らぐ数学の基礎

現代の数学の基礎は揺るぎないものと信じられている。

現代の数学者たちは、数学の基礎に重きをおかず、「数学基礎論、数理論理学なんて数学じゃない」あるいは、「数学基礎論、数理論理学なん低級数学だ」という態度をとる人が多いことは、すでに説明したが、その一つの理由が、これのことにある。

つまり、ラッセルたち数理論理学者の努力により、数学をするに十分な、揺るぎない基礎が、随分前に出来上がっていて、解析学、代数学、幾何学などの「普通の数学」を行なうには、それで十分であるために、もう研究する必要などないと思われているからといえる。

パリの下水道は、19世紀ころには、ほぼ完成していて、それが「花の都パリ」の衛生の基礎を支えていた。それは世界に誇る設備だったが、現代では、観光ツアーはあるものの、取り立てて語るべきものでもない。

そして、現代のパリの下水道は、19世紀に完成したものが、ほぼ、そのまま使われているといわれる。

これから紹介する、19世紀から20世紀前半にかけて作られた「集合論と論理による数学の基礎」も、このパリの下水道システムと同じようなものともいえる。

それがないと途端にパリの現代的生活は成り立たなくなる。数学でも同じく、「集合論と論理による数学の基礎」がなくなると、とたんに数学は麻痺する。

だから、これをあまりにバカにするのは上品な態度とは言えない。

それはともかく、その「数学を支える近代的下水道システム」としての「集合論と論理による数学の基礎」以前、どれだけ数学の基礎が揺らいでいたかを、2つの例を使って説明する。

その一つは「解析学の基礎」、そして、もうひとつは「リーマン面」の理論。

揺らぐ数学の基礎　解析学の場合

高校で、集合というものを習った人が多いと思う。たとえば、数学Aの集合と論理。これの高度なのが、集合論、論理学、数理論理学。

高校で習うものは、簡単な用語の使い方のレベルで終わっているが、大学以後の数学では、集合は20世紀以後、数学に必須の言語となっている。一方で、この資料で「論理学」と書いている学問、アリストテレス論理学、伝統論学などと呼ばれている学問は、今でも哲学や文系の教養の一部なので数学で使われることはない。また、数理論理学を普通の数学者が使うことは、まずない。

実は、数学者の圧倒的多数は、集合論の初歩は知っているが、数理論理学は知らないのが普通。そればかりか、数理論理学などは数学ではない、または、劣等な数学だ、という意見さえ日本の数学界では少なくない。

この意見は極端すぎると思うが、しかし、そういう意見が出るのには理由がある。それが実は、この講義のポイントと深く関連している。

実は、集合論とは、19世紀の後半位から、数学に必要となった哲学的、論理学的概念を、哲学から切り離して、数学に持ってきたものと考えることができるのである。

最初に集合の話を聞いたときに、それまでの算数や数学と大きく違っていて、驚いた人も多いだろうと思うが、これがその理由。

いってみれば、哲学という王国の領土の一部を本土から切り離して、数学という共和国に併合したようなもの。最近でも、クリミヤ半島のロシア併合で大騒ぎになったように、こういう乱暴なことをすれば、当然、色々な軋轢が生まれる。実は、そういう軋轢を最終的に収束させたのが、不完全性定理なのである。

その話は、段々と説明していくことになるが、まずは、元は哲学であったと言える集合論というものが、数学の中で市民権を持って行った、その歴史的プロセスを説明する。

なぜ、集合論の様なものが、数学で必要となったか、それは、上で見た、ラッセルの The Principles of Mathematics のChapter 1, section 3 の議論を見ると解る。

ここで、ラッセルは、次のように言っている：

The Philosophy of Mathematics has been hitherto as controversial, obscure and unprogressive as the other branches of philosophy. Although it was generally agreed that mathematics is in some sense true, philosophers disputed as to what mathematical propositions really meant: although something was true, no two people were agreed as to what it was that was true, and if something was known no one knew what it was that was known. So long, however, as this was doubtful, it could hardly be said that any certain and exact knowledge was to be obtained in mathematics. We find, accordingly, that idealists have tended more and more to regard all mathematics as dealing with mere appearance, while empiricists have held everything mathematical to be approximation to some exact truth about which they had nothing to tell us. This state of things, it must be confessed, was thoroughly unsatisfactory. Philosophy asks of Mathematics: What does it mean? Mathematics in the past was unable to answer, and Philosophy answered by introducing the totally irrelevant notion of mind. But now Mathematics is able to answer, so far at least as to reduce the whole of its propositions to certain fundamental notions of logic. At this point, the discussion must be resumed by Philosophy. I shall endeavour to indicate what are the fundamental notions involved, to prove at length that no others occur in mathematics, and to point out briefly the philosophical difficulties involved in the analysis of these notions. A complete treatment of these difficulties would involve a treatise on Logic, which will not be found in the following pages.


凡その意味：数学の哲学は、論争の的であり、曖昧で、数学の哲学以外の哲学の分野同様に、進歩が無いものだった。数学は、何らかの意味で真理であるということについては合意されていたと言えるものの、哲学者は数学の命題が一体何を言いしているのかということについて、合意にいたることはなかった。観念論者（idealist)は、数学は単なる形式を扱うものだと言い、経験論者は、数学は、真理への近似だと言う。哲学は数学に、数学は一体何を意味しているのだと問いかけたものの、数学はそれに答えることができなかった。しかし、今や、数学は、こういう哲学の問いかけに、数学の命題を、ある一定の論理学の基本的概念に還元することにより、答えることができるようになったのである。

注. "to prove at length that no others occur in mathematics" という部分は、哲学者のカントが言ったように、数学では分析的な論理だけでなくて、常にアプリオリな直観が必要だという説は、間違いだという意味。no others occur というのが論理しか使わないでできるということを主張している。しかし、実際には、このラッセルの主張は間違いだと後にわかる。また、 "A complete treatment of these difficulties would involve a treatise on Logic, which will not be found in the following pages"　というのは、 結局は出版されることがなかった、この本の第二巻で、A complete treatment of these difficultie を扱うという意味。この these difficulties でラッセルが意味していたのが何か、これは良くわからない。

つまり、ラッセルは、哲学者の目で見れば、数学の（哲学的）基礎は揺らいでいるではないかと言っているのである。そして、その基礎は、数学を完全に論理にだけ還元することで解決できて、それはカント哲学の主張が間違えていることの証拠だと、言っている。これは、今の数学が持たれている安定したイメージに程遠いが、実際に、20世紀の初頭までは、数学はこういう状況にあった。そして、その揺らいでいる基礎は、哲学者から見て問題だっただけでなく、数学の健全な発展を阻害する要因にさえなっていた。数学者によって何が正しいのか、標準のようなものができず、それこそ、ある数学の定理が正しい、いや、それは証明が変だ、というような議論が実際に、色々なレベルで行われていたのである。

そういう不安定な状況は、後で説明する様に、19世紀ころには、幾何や代数など数学の色々な分野であったのだが、特に古くから有名で広く知られているのが、解析学の基礎、高校の数学の用語で言えば、微分・積分の基礎だった。

微積分学、解析学では、例えば無限級数というものが考えられて、それが収束する値が議論される。たとえば、「高校数学応援ブログ web 問題集」から。

上のリンクで分かるように、これは大学入試（特に理系）で出題されるような問題。高校でやるように、これを直観的にやると、時々良くわからないことが起きる。

たとえば、１－１＋１－１＋１－１＋…　という無限級数。上の「高校数学応援ブログ web 問題集」の説明からすると、これは、1, 1-1, 1-1+1,.... という数列の収束で考えれば良いことになるので、1, 0, 1, 0,.... という数列になり、この無限級数は振動していることがわかる。

しかし、昔の人は、１－１＋１－１＋１－１＋…　のような無限級数を、１－１＋１－１＋１のような有限の式の無限版と考えたので、有限の時の式計算と同じことができるはずだと考えた。
そのため、

　　１－１＋１－１＋１－１＋…　　=　（１－１）＋（１－１）＋（１－１）＋…　＝　0+0+0+…　＝　０

　　１－１＋１－１＋１－１＋…　　=　１＋（－１＋１）＋（－１＋１）＋（－１＋１）＋…　＝　１＋0+0+0+…　＝　１

と計算して、0=1 となり不思議だとか、これは無から有を生むものだ、とか考えたりした。

そして、こういうものが、哲学者によって批判されたりしていた。

コーシーの解析学教程

こういう混乱した解析学（微積分学）の状況を最初に改善したのが、 ナポレオン時代直後の1821年, パリの技術者養成校エコール・ポリテクニーク（理工科学校）で書かれた教科書の一つであるコーシーの「解析学教程」だった。

コーシー以前の数学者は、微積分学の創始者の一人、ライプニッツを含めて、ｄｘ　などと書かれる無限小という、ゼロではないが、無限に小さいという数学的存在を考え、それを使って微分をしていた。そして、ｄｘ　が無限小だったら、1/dx は、どのような数より大きい無限大だった。これがバークレイ僧正などの哲学者から批判を浴びていた。また、上の０＝１のように、どう考えればよいかわからない数学の問題がでてくる原因となっていた。

そこで、コーシーは、無限大、無限小を考えるのを止めて、「高校数学応援ブログ web 問題集」の様に、無限大や無限小は、収束する有限のものの列だと考えた。たとえば、1,1/2, 1/4, 1/8, 1/16,　…のように半減していく数列は0に収束する。無限小というのは、こういうものだと考えた。こう考えると、これの収束する極限を dx と書けば、実は、1/dx は、 1, 2, 4, 8, 16,…となるから、それは無限に大きくなる「無限大」だと合理的に説明ができる。

ラッセルは、数学者は、自分たちが議論している「真理」や対象が何なのかを説明できないと書いているが、すくなくとも、無限小、無限大という、神秘的とさえいえるものは、これにより大幅に追放することができた。ラッセルは、同じ数学の命題のもつ意味というものが、観念論者と経験論者では、異なって説明され、ふたり人がいたら、合意することができない、という意味のことを書いているが、解析学の命題を巡って、賛成派、反対派の意見対立が起きるようなことは、このコーシーの解析学教程のお蔭で非常に減った。

しかし、そのコーシーの方法でさえ、答えることができない問題が存在した。たとえば、コーシーの時代には、連続な関数は、この例の場合のｘ＝０の時の様に、例外を除くと、微分可能であると広く信じられていたが、それが正しいかどうか、コーシーの方法で判定することは難しかった。

それを可能にしたのが、次に説明するワイエルシュトラスの方法。

ワイエルシュトラスの方法

ドイツの数学者ワイエルシュトラスは、コーシーが無限小を、ドンドン小さくなる（ゼロに収束する）列、あるいは、変量（変化する量）と考えたのに対し、「ドンドン小さくなる」という性質を、数と論理だけを使って定義した。

それをイプシロン・デルタ論法という。高校数学の美しい物語の説明。

最初の、

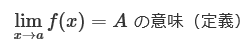
の　A　がゼロの場合に、f(x) が無限小の代わりになる。

そしての、この式の定義は、



であった。

数と論理だけを使って、と書いたが、この文章の日本語の部分が「論理の部分」、つまり、次の部分


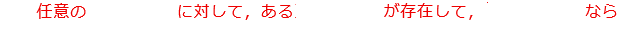
そして、残りが「数の部分」、つまり、次の部分


「論理の部分」は、「任意の（すべての）＊＊に対して」、「ある＊＊が存在して」、「なら（ならば）」の様な、フレーズが使われていて、これはすべて「論理学」で使われる表現になっている。

一方で、「数の部分」は、「正の実数」とか不等式の様に、高校までの数学で勉強した実数の概念や数式。

「論理の部分」、つまり、論理学の部分は、人間が数学だけでなく、日常に推論する時につかうもの。

有名なものとしては、次の三段論法がある：

ソクラテスは人である。
すべての人は死ぬ者である。
よって、
ソクラテスは死ぬ者である。

これは古代ギリシャの哲学者アリストテレスが創始した「伝統論理学」とか「アリストテレス論理学」における、三段論法、シロギズムと呼ばれる、推論の理論の有名な例。

ラッセルは、このシロギズムを、数理論理学というもので数学化したのだが、ワイエルシュトラスは、日常的な推論に頼った。

伝統論理学のシロギズムは、日常的な推論の理論だと考えられていたので、言い換えれば、

ワイエルシュトラスの方法とは、コーシーの解析学教程における「収束」の概念を、数の理論と伝統論理学に帰着させるものと言える。

この方法のお蔭で、ワイエルシュトラスは、コーシーが解決できなかった、連続と微分可能性の問題を解くことができた。

その結果、彼が作った有名な関数が、ワイエルシュトラス関数。

コーシーの時代には、連続な関数は、有限個の例外点を除いて、殆どの点で微分可能になると信じられていた。

しかし、ワイエルシュトラス関数は、連続だが、あらゆる点で微分できない関数だった。

こういうものを作り出して、また、それが連続であるとか、どの点でも微分できない、と証明するには、ワイエルシュトラスの方法がないとできなかった。

ワイエルシュトラスの方法において、漸く、解析学、あるいは、微積分学の「揺らぐ基礎」が、確固たる基礎に置き換えられたと言える。

高校で、あまり微積分をやってない人には、難しかっただろうが、要するには、次のことさえ理解できたならば十分：

　　　微積分の基礎は、最初揺らいでいたが、コーシーとワイエルシュトラスの努力により、数の理論（実数の理論）と論理（人間の常識的推論能力、あるいは、伝統論理学）による、確固たる基礎ができた。

揺らぐ数学の基礎　リーマン面の場合

数学には、複素関数論という分野がある。数学には、ノーベル賞がないが、フィールズ賞という、それに「数学のノーベル賞」がある。

日本人で、フィールズ賞を受賞した人が、いままでに3名いて、その内の二人広中平祐（1970年）、森重文（1990年）は、京大の数学科の出身者。

しかし、最初の日本人フィールズ賞受賞者は、東大出身の小平邦彦（1954年）だった。

この小平の主な研究分野が複素関数論（多変数）。

現在の高校では、数3で複素平面というものをやるが、それを知らないと、この分野を説明するのは不可能。

複素平面を知らない人は、以下の説明の斜体の部分は無視して、画像や動画でみせる平方根のリーマン面と呼ばれる不思議な「幾何学的存在」が、複素関数論という分野で必要になった、しかし、その不思議なリーマン面が何なのか、どの様に「存在する」のかは、それを考え出したリーマン自身も全く説明ができなかった、ということだけ理解しておけばよい。

リーマン面の概念

リーマン面は、ドイツの数学者ベルンハルト・リーマンが、彼の複素関数理論の中で生み出し、後の多様体論という幾何学理論に繋がった19-20世紀数学史上における非常に重要な概念。

それを非常に単純な場合である、平方根の場合に説明する。

２次関数y=x2の逆関数は、x=+√yと、x=-√yの２つがあり、これを y に対して、x が二つ決まる、つまり、+√y と -√y の両方が値となる「２値関数」とみる立場もある。

しかし、リーマンは、この x, y が複素数までに拡張されているときには、y が、２つの複素平面の上を動くと考え、その一枚では+√y を値として、もう一枚では -√yを値とすると考えると、値が一つの普通の関数になり、色々と数学的に都合が良いことを発見した。

ただし、その時、この２つの複素平面を「切り貼り」して、１枚の「面」にする必要があった。

そうやって出来たものが「平方根のリーマン面」である。

微分の概念は、複素関数、つまり、複素数を入力として、複素数を出力とする複素数の関数に拡張できるが、嘘を承知で言えば、その様な「微分可能な複素数の関数」の理論が、複素関数論。

その複素関数論では、平方根とか、あるいは対数とか、ある微分可能な複素数の関数の逆関数で重要なものが沢山ある。

それらの多くは、値が沢山ある多値関数なのだが、それを一値にする手法がリーマン面。

それは、単に「一値にできる」というようなことでなく、そういうリーマン面の幾何学的特性で、実に色々なことが分かる理論であった。

ともかく、平方根のリーマン面というのは、次のような「形」をしている「面」：

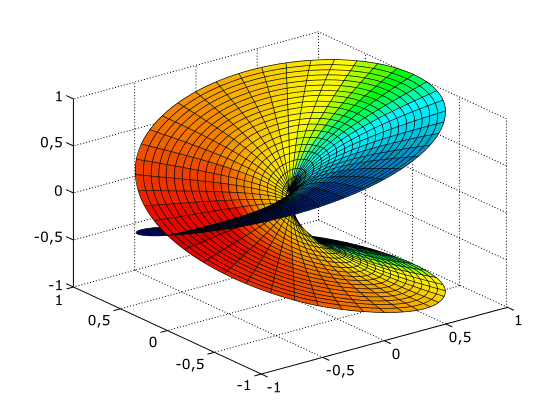
ポイントは、面が自分自身を横断している点。

正確にいうと、「横断している様に見えるだけで、本当は横断してない」と考える。

実は、このリーマン面は三次元空間の曲面として作図するのは不可能なもので、それを無理矢理描くために、このように面が面を横断してしまう。

その作り方は、次の動画のようにする：

平方根のリーマン面の作り方
簡単に動画を説明すると、２つの円盤を用意し（それが２つの複素平面だと思う）、中心から切り込みを入れる。

そして、その切り込みの（すぐ）上の面を、もう一つの円盤の切り込みの（すぐ）下の面に繋ぐ。

２つの円盤に上の面と下の面があるので、総計４面あるが、ひとつの円盤Aの上の面をもう一つの円盤Bの下の面に繋ぐと、それが邪魔して、最初の円盤Aの下の面を、もう一つの円盤B上の面につなぐことはできない。

しかし、それを無理矢理できたと思うと、次のような面ができたことになる：

平方根のリーマン面の「完成品」

リーマン面が自分を横断しているように見えるが、実はよく見ると黄色のポストイットを切断して、セロテープで固定していることがわかる。（＾＾；）
この「完成品」を静止画で３方向から撮ったもの: