
2015.06.01版:クラスという用語と term という用語の関係を説明するのを忘れていました。このためアリストテレス論理学とクラスの関係が解らないような資料になっていました。そのため2か所に変更を加えました。変更箇所1、変更箇所2
3については、この資料の最後で、すこし補足をします。
プラトンは、「本質」のようなものが、我々の生々流転する世界の背景にあり、それがイデアの世界だと考えた。
というより、むしろ、そちらの方が真の存在だとプラトンは考えた。(有名な洞窟の比喩:興味のある人はこちらを参照)
そういう真の存在としての理想の存在がイデア。
プラトンのイデアのモデルは、数学だったと言われている。数学者は数や、代数構造、高次元空間、層、圏などと呼ばれる極めて抽象的な存在をあたかも目の前にあるように感じて考えている。時には手を出して掴むことさえある(林の経験。掴みながら考えると分かり易くなる。)
例えば、層という概念の内の、連続関数や正則関数の芽の層、などというものは、ある意味で無限次元空間、などというと次元が足りないくらいに複雑で抽象的なもの。数学を実際にやったことがない人には断片的な想像すら難しい存在。しかし、林は、これと論理学の関係を研究していた1980年代(20代)のころは、これを黒板に書いて、仲間と議論をしていた。
こういうものに人間は慣れる。
こういう「慣れ」の存在は「抽象的概念」だけではない。Brain Computer Interface (ブレイン・マシン・インターフェースともいう。Wikipedia)という工学・心理学の分野があり、考えただけでロボットのアームを動かすことができるようになっている。デモ。まるで念力!IT魔術説の他の一例。
この分野では最初、人間が腕や手をコントロールするやり方を神経の働きのパターンとして検出し、それで機械を動かそうとしていた。ところが、数年前、アメリカの研究グループが、「自然状態」では人間の頭脳には備わっていないパターンのコントロールの方式を、人間の脳が学習して作ってしまうということを発見した。たとえば、さっきのデモでは、人間が頭脳の中の思考で(多分、腕の神経や筋肉の電気信号などもつかっているらしいが)、自分に本来備わっている5本の指の様に、ロボットの指を動かしていた。これが8本の指とか、指ではなくて電動ドリルのような工具とかを、自分の肉体の一部のように動かす能力を、機械と頭脳の間のインターフェースをつけて訓練すると、頭脳が作り上げてしまえるということ。これは道具を身体の一部のように使いこなす「職人」と呼ばれる人たちの存在や、自分が自転車などを乗りこなしているとこの感覚を思い出せば、実は、それほど非日常的なものでないことがわかる。
人間の頭脳には数学の抽象概念とか実際には機械や器械である「身体の一部」など、「この世のものではないもの」を、「この世のもの」と同じように感じ扱える能力があるらしい。
その様な状態になると、数学者の様に寝ても覚めても数学の世界に浸っている場合は、抽象の方が普通の意味での具体より、より具体的になるし、義足を体の一部だと思ってしまう。
この「現実の世」にない理想が、我々の目の前にあるスクリーンや机と同じように「存在する」と言ったのがプラトンで、それには違和感が伴う人が多いのだが、一度、自分で経験してみると、現実感が生まれ当たり前と感じるが、自分で経験しない限り、この感覚は分かり辛い。
イデアには、たとえば、一般名詞「人間」であらわせるようなもののイデアもあるが、「赤のイデア」のような形容詞が表すもののイデアもある。
そして、この赤い文字列と、この赤い文字列は二か所にあるので、別の「赤い文字列」だが、「赤い」のイデア、さらに言えば「赤のイデア」を共有していると考えた。
上の二つの赤い文字列は、赤のイデアを分有している文字列である。その故に、それは赤い。
ドイツ語の Wikipedia の項目 Ideenlhere の図を使って説明する。
その図とは、次のもの。ただし、Ideen Gegenstände という単語より上の部分は説明しない。この上の部分は認識論に関係する部分なのだが、この講義では存在論・形而上学だけを問題にし、認識論部分は考察しないため。

この資料の上の方にある和訳の表:
個々の人(アメリカ大統領のオバマ、私、あなた、…)、個々の三角形は、Gegenstände: 対象と呼ばれる存在である。
この対象の様な現実的・現世的 vergänglich なものに対して、Ideen (Idee の複数形) 、イデアは、非現世的 unvergänglich である。
対象は、人が個性をもち、様々であり、また、成長したり老衰するように、常ならぬもの veränderlich である。
これに対して非現世的なイデアは、unveränderlich、つまり、成長も老衰もしない、変化せず絶対的な存在である。
個々の対象である個々人が、人である所以は、一個一個の対象としての人が、人のイデアという存在に分有する teilhaben, participate からである。
これは、逆に言えば人のイデアが、一つの対象である個人に現実化 Gegenwärtigkeit していると言える。
その意味は、原像、原型 Urbild であるイデアから、その一つの像 Abbild としの対象が生まれているのである。
ところがプラトンの弟子アリストテレスは、このイデア論を次のように批判した。
Plato's theory of forms claims to explain the nature of things but in fact the abstract forms are only useless copies of actual things, and fail to provide any explanation of the existence and changes of concrete things; Plato's theory of forms sets up an unbridgeable gap, a dualism between the world of intelligible ideas and the world of sensible things; the theory makes it impossible to explain how sensible things and intelligible forms are related at all.
要旨:プラトンの様に形式(イデア)中心だと、現実と理論が乖離してしまい、形式(イデア)の理論で現実が説明できる根拠がなくなるではないか?
また、プラトン自身が書き記しているThird Man Argumentと呼ばれる批判もあった。
これらの批判のもとに、アリストテレスは、プラトンのイデアを、対象(オブジェクト)の集合、哲学の言葉でいうとクラスに置き換えた。
そうして出来たものが、アリストテレス論理学と呼ばれているもの。

この図で、人の写真の周りに、「線引き」がしてあって、人と人でないものを分けている。この外と内を分ける線は一種の境界、壁、柵のようなもので、これが西洋の論理に特有の term (ラテン語 terminus, 古代ギリシャ語 horos)という概念をシンボライズしている。
要するに、特定の対象(複数でも単数でもよい)を、それ以外と分かち、その分別したものに名称を与えたものが term 名辞だと思えば良い。(歯切れが悪いのは、Port-Royal 論理学では、これに明瞭な定義がないから。これは後で見る。)
6月1日追加(ここから、次のパラグラフ先頭の「しかし、」まで):「名称を与えたもの」と言う所を無視すれば、term とは、高校までの数学で学習した、集合、現代の記号論理学のさきがけとなった1903年のバートランド・ラッセル著 The Principles of Mathematics の用語を使えば class であると考えられる。集合ならば、数学的なのだから、イデア論のような「神秘的」な要素はないはずで、アリストテレスは、現代では数学の一部となっている集合という概念でイデアを置き換えようとしたと考えられる。それがアリストテレス論理学。
しかし、そのアリストテレス論理学も、実はイデア的なものを完全には払拭していなかった。
それがポール・ロワイヤル論理学に見られる compréhension という概念。
compréhension は、étendue と対をなす概念。この対を以下で説明する。
この対概念の説明の原文は、Google Books でのフランス語のポール・ロワイヤル論理学1763年版で読める。しかし、林はフランス語がダメなので、英語でやります。
これが英語だと、 comprehension (内包)と、extension, extent (外延)になる。
これを標準的伝統的論理学の最初のスタンダードとされている、17世紀のポール・ロワイヤル論理学の英訳(Google books で完全に読めるもの)と、京大内で閲覧できる別の英訳(電子書籍)で確認する(後者は、古い活字なので、s が f のように見えることに注意)。
Google Books の方の英訳
Kuline から読める電子アーカイブ、
要するには、comprehension というのは、三角形の様な概念が持つ属性 attributes の総体。我々は後に、この属性 attributes という言葉を Java などのオブジェクト指向言語の説明で見ることになる。
一方で、extension, extent というのは、個々の三角形の総体。つまり、高校数学(数学A?)で習った「三角形の集合」のことだと思えばよい。あるいはラッセルの用語でいえば「三角形のクラス」。(この一文、6月1日に追加:)
高校のとき、おそらく、集合の内包的定義、外延的定義、というのを学習したのではないかと思う。
しかし、extension の方は、集合という概念を納得していれば、納得できるが、comprehensionというものは、なんとなく座り心地が悪い。Triangle の comprehension の説明で、最後が、etc. となっているように、何が attributes なのかと言われてもはっきりと答えられない。
一方で、extension 外延の方は、高校数学を知っていれば、直にわかる。特に、有限個の対象しかない場合には、イデア論の the third man argument のビデオで見た、人を囲む線をイメージすれば、その意味が納得できる。つまり、高校数学でならう、いわゆるベン図 Venn diagramと同じものになっている。
先に、term 名辞についての歯切れの悪い説明をした。これを詳しく見る。
最初に言語上の注意:英語ではイデア論を theory of forms といい、idea は日本語でいう「イデア」の意味ではあまり使われない。たとえば、このスタンフォード大の哲学百科事典のプラトンの項目での idea という単語の使われ方を参照。
この項目のタイトル「Term, Idea: イデアの代替物」の idea は、プラトンのイデアではなく、上で comprehension, extent の説明の文章に出てきていた comprehension of the (an) idea, extent (extension) of the (an) idea の idea。たとえば、triangle という概念。
上に引用した1717年版のPort-Royal 論理学の59ページを見ると、term という言葉が、この idea と同じように使われている。しかも、検索してみると、それは term という言葉の初出であることがわかる。
プラトンのイデアは、唯物論的になっている現在の思考方法からは、気持ちが悪い、理解しがたいものだが、この term という言葉も実は理解が難しい。少なくとも、歯切れのよい定義ができない。
しかし、これがアリストテレス論理学の基礎であり、アリストテレス論理学は、Term Logic という別名さえ持つ。
元祖 Port-Royal 論理学には、定義や説明がないので、使われ方から、その意味を理解するしかない。また、この用語は、色々に定義されており、また、ヨーロッパの言語や文化と深く関係している。たとえば、この19世紀(1850年)の教本では、term を音声と関連づけて説明している。これは、言語は発話が基本であるというヨーロッパの言語観を反映している。
ここでは、20世紀における標準的な説明と思われる、スタンフォード大の Encyclopedia of Philosophy の Aristotle's logic という項目の解説を使う:
Subjects and predicates of assertions are terms. A term (horos) can be either individual, e.g.Socrates, Plato or universal, e.g. human, horse, animal, white. Subjects may be either individual or universal, but predicates can only be universals: Socrates is human, Plato is not a horse,horses are animals, humans are not horses.
つまり、名辞 term は、二種類からなる:
そして,これら二つを合わせて
と呼ぶこともある.特称名辞は,一つの「者」しか表さないが,それでも何かが集まっているもの,ただし,ひとつしか集まってないもの,と考えるということ.
集合名辞は、ひとつでもあり得る、が、集まりをあらわすもの。これが、Term Logic の、非常に大きな特徴。
例で、この考え方を説明してみよう。








実はこの様に考えると、英語の
の様な文章と
が同じ種類の文章、あるいは、命題として考えることができる。
たとえば、
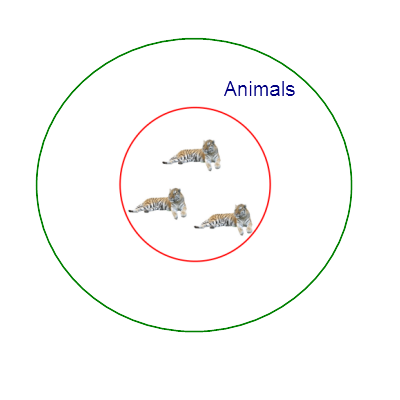
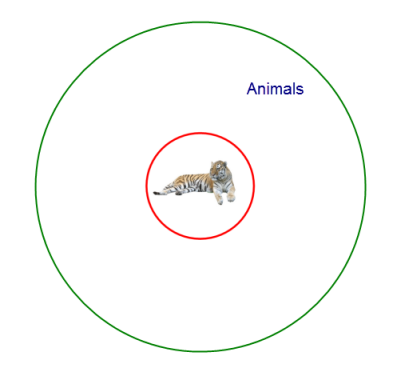
この様に考えると、有名な三段論法
の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ
の形であることがわかる。
日本語は、この形が基本ではないことに注意!
以上では、term の概念を、集合、つまり、正確に言えば、term の extent で説明した。しかし、これは高校数学で集合を勉強しているみなさんに教えるための方便のようなもので、正確に言うと、 term は集合そのものではなくて、あくまで言語表現を伴うもの。
そのことを如実に物語るのが、Species infima という考え方。これを説明するために、genus, species, difference という概念を説明する。
先ほど、two tigers と three tigers の包含関係を考えたが、二つの universal term の間に同様の包含関係がある場合、含まれる方を Species (種)、含む方を Genus (属)と呼ぶ。
たとえば、tiger 虎 という term は、animal 動物 に対して species であるし、animal は、tiger に対して genus となる。
そして、species にはなるが、genus にはならない term を Species infima と呼ぶ。
ただし、これは Port-Royal 論理学のオリジナルにはない用語。19世紀のある本で見ると、greyhound が Species infima だとある。
しかし、同時に、この犬種を色とか出身地で分類していくと Species infima でなくなると注意している。
実際に、こういうことが最近起きた例。
鮭児(けいじ)は、この15~20年ほど前にできた言葉だと説明されているので、シロザケ、あるいは、普通に日本語で鮭という term は、比較的最近に Species infima でなくなったことになる。
では、この鮭児を、一般のサケ、シロザケから分かつ(分別する)ものは何か?
このページを見てみると、生まれた場所、脂肪の比率、大きさなど、様々な特有の属性が列挙されている。
この様に、ある term に、さらなる属性を追加して、そのtermの範囲を狭めて species を作るとき、この追加する属性(複数でもよい)を、difference 種差という。
これまでは、たとえなどに使ったりしたが、ITの話はしておらず、伝統論理学の話だった。次回からは、伝統論理学の考え方と比べるITの概念オブジェクト指向アーキテクチャの話をする。
伝統論理学には、これ以外に四原因説(これは後にやります)や三段論法の理論など、様々な要素があるが、次回から示していく、オブジェクト指向アーキテクチャとの比較では、この範囲の知識で済む。
ただし、その前に、質問票へ回答のため資料の三番目を補足する形で、イデア論のもう一つの気持ち悪さを論じておく。
実は、これがオブジェクト指向で起きる。つまり、オブジェクト指向アーキテクチャはアリストテレス論理学に似ているだけでなく、一部、プラトンに先祖がえりしていると言える。
質問票への回答のための資料の3番目
それへの補足: