
(12.03 間違い訂正。「偽かつ真」の値が「真」になっていたのを「偽」に訂正)
名辞という概念が、もっとも重要なポイント。
名辞は英語では term。だから、これが重要となる論理なので、アリストテレス論理学のことを Term logic ともいう。
尾崎の教科書の10-11頁に次のような名辞の例が書かれている:
尾崎は,1のような名辞を「唯一個の人あるいは一個の事物を指言する者」と説明し,2のような名辞を「諸種の馬,諸国の王,諸方の府県会を指言する者」と説明し,それぞれ,
と名づけている.
そして,これら二つを合わせて
と名づけている.特称名辞は,一つの「者」しか表さないが,それでも何かが集まっているもの,ただし,ひとつしか集まってないもの,と考えるということ.
名辞と名詞を混同するという「方便」からすれば、
両方を合わせれば
というものが考えられるということになるが、文法用語では、集合名詞とは、information, furniture, software などの集合的に用いられ名詞。
集合名辞は、これとは違っていて、ひとつでもあり得る、が、集まりをあらわすもの。これが、Term Logic の、非常に大きな特徴。
例で、この考え方を説明してみよう。








実はこの様に考えると、英語の
の様な文章と
が同じ種類の文章、あるいは、命題として考えることができる。
たとえば、
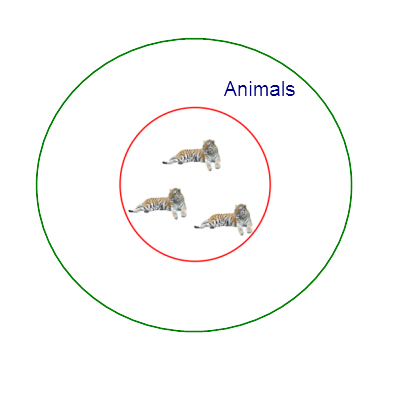
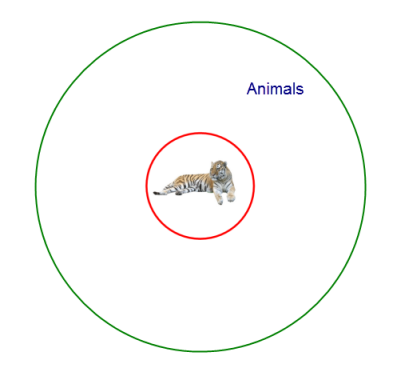
この様に考えると、有名な三段論法
の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ
の形であることがわかる。
日本語は、この形が基本ではないことに注意!
つまり、アリストテレス論理学というのは英語、ドイツ語、ギリシャ語などの欧州の言語の構造に強く根ざしている。
片仮名漢字交じり文の中に、用例としての平仮名漢字交じり文が入っているので注意。しかも、合略仮名 コト(19頁1行目下から5文字目)を使ったり、同じ平仮名の異なる崩し字を使うなどしているので大変読みにくいが、言っていることは簡単:
しかし、命題は,この「―は―なり」の形だけではない.この形の命題は全称肯定命題と呼ばれるもの.命題は,全称v.s.特称,肯定v.s.否定の2つの対立軸を使い,全部で4種類考えられる.(21-22頁)
上記4パターンを示す図 http://en.wikipedia.org/wiki/Square_of_opposition
このようにすると「ソクラテスは人である」「人は死ぬものである」「ソクラテスは死ぬものである」 という,有名な三段論法にでてくる命題が,すべて同じ種類の連辞(英語なら is, are...)から,できるという,大きな長所がある.
「命題は,この「―は―なり」の形だけではない」と書いたが、少し無理をすると、上の4パターンすべてが、この形だともいえる。(ここは、まとめでなく新しい説明)
Noone is there. これも
これが日本語では、
となって「ない」という否定が、一番外がないにある。日本語には、もともと、nobody とか noone というような表現がない。また、non-... にあたる「非-...」は漢語であって大和言葉ではない。大和言葉ならば「...にあらず」だろう。つまり、文全体に否定がかかっていて、SやPが単独で否定されることがない。
この様に、アリストテレス論理学の基本構造は、ラテン語などのヨーロッパの言語の特徴(多分、インド・ヨーロッパ語族の特徴)を反映している。
しかし、これは単に言語の問題ではなくて、世界観の問題ともいえる。
実は、英語 term の元は、ラテン語の terminus、これが古代ギリシャ語では horos となる。
そして、この horos という言葉は、個々の対象物、物、Gegenstand と、それ以外を分け隔てる「境界」「壁」 boundary を意味していた。
このことへの違和感が西田の述語に向かう論理の大きな動機になっている。また、京都学派の哲学を貫く大きなモチーフになっている。
西洋の論理学者、哲学者は、この様な「二つの名辞の関係」で論理学を組み立てて、命題を分類し、さらには可能な推論をパターンで分類した。
それをシロギズムという。この話は凄くややこしいので、一部分だけ簡単に説明。
先ほどの三段論法の前提、つまり、1-3の内の、1と2
の状況を、今までのようなベン図で重ねて図示してみると
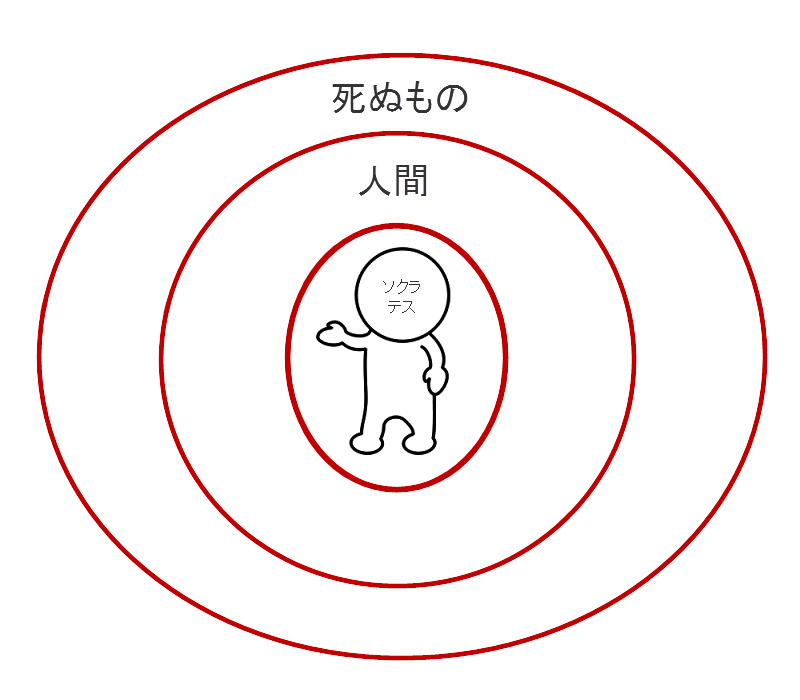
となる。これは
がどちらも全称肯定命題として理解されたとき、 A be B B be C の、中間の B をとって作った A be C という全称肯命題は、二つの前提が正しいときには正しいことを意味している。
同様のことを、1,2 と A be C のそれぞれを、全称肯定、全称否定、特称肯定、特称否定のすべてのパターンで考えて、その推論が正しいかどうかを、ひとつひとつ検討したもの。
図を見ただけでわかると思うが、兎に角、ややこしい…
で、その欠点を、「述語」の概念を取り入れることにより、解決したのが、数理論理学、記号論理学の体系である述語論理学。
これでどうして前回、あのおもしろい動画を見たのかが明らかになる。この二つのものは、どちらも「述語」と言っているが…
そして、これとかなり違う理由で、アリストテレス論理学の S be P の形式を乗り越えようとした人たちがいた。そして、その人たちの努力が記号論理学につながった。
そして、その一人が、最初のころに、そのビデオを見たバートランド・ラッセルであり、また、その努力の結果といのが、40歳ころまでの「宗教の代替物」であったプリンキピア・マテマティカ。
しばらく、これの話をする。まずは、なぜ記号論理学は必要だったかという話から。
アリストテレス論理学は、実に長い間、西洋では思考の基本様態、あるいは、それに近いものとして考えられていた。しかし、それを、本当の推論に適用しようとすると、実は、シロギズムの説明でみたように、実にややこしい。
実は、それだけでなくて、普通の日常生活で使う文章を、たとえ、S be P を基本とする英語の場合でも、アリストテレス論理学の形式で表現しようとすると、色々と困難にぶつかる。特に、それは、人と人との関係性、ものとものとの関係性などの「関係」を表現しようとすると、大変に不自然な表現になることがわかる。
たとえば、下のジャズ Everybody loves my baby. の歌詞の赤字の部分を、S be P で記述してみよう。
歌詞:http://www.youtube.com/watch?v=V42uJKhoe2I
I'm as happy as a King,
Feelin' good n' everything
I'm just like a bird in Spring,
Got to let it out.
It's my sweetie, can't you guess?
Wild about her, I'll confess!
Does she love me?
Oh my, yes!
That's just why I shout:
Everybody loves my baby,
But my baby don't love nobody but me.
Nobody but me.
Everybody wants my baby,
But my baby don't want nobody but me
That's plain to see.
以下略
つまり、次の二つの文章を S be P にする。
(but が消えて、カンマがピリオドになっているが、こういうものは論理的内容には影響を与えないと考える。)
1.Everybody loves my baby,
2.But my baby don't love nobody but me.
の1は、尾崎の「花なきものなり」を、"non-flower plants"としたテクニックを使って、
all persons are "my baby"-lovers.
と書ける。
2は、内容的には、次の二つの文章と同じ。
2.1. my baby don't love anybody who is not me.
2.2. my baby loves me
2.2 は、1と同じテクニックを使って、
my baby is a me-lover.
2.1 は全称否定にすればよさそうなので、
my baby is non-P
だろうと推測できる。元の英文と比べて考えると
my baby is non-((anyone who is not me)-lover).
となる。ちょっと言い方を変えて
my baby is non-((non-me)-lover).
この様に、A loves B などのような、二者の関係をアリストテレス論理学で表そうとすると非常に不自然なことになることが多い。
その直観的理由としては、アリストテレス論理学が、個を出発点として、その terminus による分類で世界を記述しようとするからである。
このことを、たとえば、20世紀初頭に、哲学が記号論理学ベースの英米系哲学と、ハイデガーなどの実存主義を中心とする大陸哲学に分かれていく、その二つの枝のルーツともいえる新カント派の哲学者、エルンスト・カッシーラーは、その著書「実体概念と関数概念」で、もともとが動物学のような分類科学をモデルにしてアリストテレス論理学が作られているからだと書いた。
これに対して、全く違う観点、動物学のような分類学ではなくて、数学をモデルにして論理学を再構成した人たちがいた。それがラッセルたち初期の記号論理学者。
ここでは、ラッセルをさらに遡り、その源流の一つとなった、アメリカの哲学者パースの論理学と、さらに、その元になった、イギリスの論理学者ブールの論理学を見ていく。
パースの論理学には、三つのポイントがあった。それは
まず、この第1のものから見よう。
A loves B
のような二つのもの関係を記述するとき、
A is a lover of B
でなくて、
A loves B
と書ければ随分楽。
他の例
A benefits B
A is a benefactor of B
パースは、このような二つのもの関係を記述するとき、
i loves j
i benefits j
を、数学の記号を使って、それぞれ
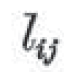
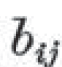
と書いた。
今ならば
L(i,j)
B(i,j)
と書く。
パースの原文を見てみる。
ここで少し脱線(しかし、学問の仕方の例としては重要な脱線)。
この例の lover, benefactor は何から来ている?
どうもしっくりこない。で、こういうときは、Google Books で検索する。
特に、こういう例は、キリスト教から来ていることが多いので、古い文献を見た方がよいが、Google Books はそれに最適。
現在では、通常の図書館では持てないような19世紀のドイツ文献などが平気でサーチされてしまう。
#ただし、京大文学研究科図書館クラスになると、Google Books にない図書を沢山所有しています。
#京大は世界の主要大学のなかでは新参者。京大よりずっと古いヨーロッパなどの大学図書館や、その他の図書館・史料館には何があるやら…
lover benefactor
で書籍をサーチすると、ビンゴ!!
トマス・アクィナス「神学大全」 Summa Theologica より (vol.3,part2.sec.2)
Twelfth Ariticle の内容は
Whether a Man Ought to Love More His Benefactor Than One He Has Benefited?
「人は施したるものより、施しを受けしものを、より愛すべきや?」
つまり、この辺りの、パースの例は、男女関係ではなく、トマス・アクィナスの論理的問答集「神学大全」における「施し」「恩」についての論理的・哲学的・神学的議論を意識していた可能性が高い。
(脱線終わり)
この様な述語の記号(述語記号)を導入すると、たとえば、
「全ての者は、誰かを愛しており、また、その者に施しをなす」
あるいは
「全ての者は、誰かを愛しており、また、その者に恩をなす」
が、
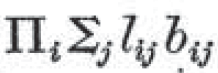
と書ける。
では、このΠとか∑は何か?
これが quanifier 量化子と呼ばれるもので、これがパースの、もう一つの大発明。
(フレーゲと)パースが行った述語の導入は、数学の関数
f(i,j)
や数列
aijのような記法にならったもの。
パースは、さらに数学の記法を論理学に応用した。
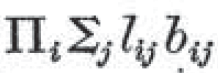
の
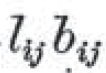
の部分は、 lij と bij の掛け算を意味している。
これは、1を真、0を偽と考えて、
1×1=1
1×0=0
0×1=0
0×0=0
となるが、これは
真かつ真 は 真
真かつ偽 は 偽
偽かつ真 は 偽
偽かつ偽 は 偽
という「かつ」の真偽の規則と一致する。
+の方は
1+1=2
1+0=1
0+1=1
0+0=0
となるが、2は1以上なので、1とみなすと、
1+1=1
1+0=1
0+1=1
0+0=0
となり、これは
真または真 は 真
真または偽 は 真
偽または真 は 真
偽または偽 は 偽
という、数学でつかわれる「または」と一致する。
さらに、マイナスを否定とみなして、
-0=1
-1=0
と定義すると、ドモルガンの法則などが成り立つ。
-(A + B) =(-A)×(-B)
-(A×B) =(-A)+(-B)
このように演算を定義した0と1の代数はブール代数と呼ばれるものの一つの例で、イギリスの数学者ジョージ・ブールが発明した。
パースは、このブールの考えをさらに発展させて量化子を論理学に導入した。
たとえば、前に考えた例
Everybody loves my baby.
を考えてみよう。これは、
All persons love my baby.
のことである。そこで、数学の変数(あるいは添え字) i が人間、つまり、persons を表すとする。すると、この文章は、
All i love my baby.
になる。さらにパースの述語記号を使い、my baby を j と書くと、これは、
All i lij
と書ける。
ところが、もし、人(persons)にすべて通し番号がついているとすると、 i や j は、0, 1, 2, 3…という数字だと思ってもよい。
もし、my baby の番号が5番だとすると、これは、
All i li5
と書ける。
ところが、これは
l05 かつ l15 かつ l25 かつ l35 かつ l45 かつ l55 かつ l65 …
つまり、ブール代数の記法では、
l05 × l15 × l25 × l35 × l45 × l55 × l65 …
つまり、
l05 l15 l25 l35 l45 l55 l65 …
のことである。
数学では、こういう数列の積を
Πi li5
と書く。これがパースのΠの意味であり、それは、「すべての i に対して、li5 である」を意味している。
同じように、以上の説明の「かつ」、つまり、ブール代数の掛け算を、ブール代数の足し算、つまり、「または」に置き換えると、
l05 または l15 または l25 または l35 または l45 または l55 または l65 …
つまり、ブール代数の記法では、
l05 + l15 + l25 + l35 + l45 + l55 + l65 …
となるが、これは数学の記号を使うと、
∑i li5
になる。これがパースの∑の意味で、それは、「ある i に対して、li5 である」を意味している。 つまり、「誰かが my baby を愛している」「ある人が存在して、その人は my baby を愛している」となる。
以上の説明から、
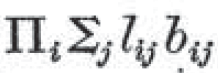
を直接的に日本語に訳してみると、
すべての人 i に対して、ある人 j が存在して、i は j を愛していて、かつ、i は j に施しをする
と読める。つまり、
全ての者は、誰かを愛しており、また、その者に恩をなす
と読める。
そこで、これを使って、「my baby が愛しているのは私だけ」を表現してみよう。
まず、7 が私の番号だとする、そうすると、この文章は、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
となる。
i はXXだ
は、等号を使うと、
i =XX
と書けるし、これは数学風だから、OKとして、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
は、
全ての者(person) i は、my baby がその者 i を愛しているならば、i = 7
となる。(7が「私」の番号!)
「ならば」は、まだブール代数の値で定義していないが、これは伝統的に、
A ならば B = -A または B
と定義することになっている。
そうすると
真ならば真 は 真
真ならば偽 は 偽
偽ならば真 は 真
偽ならば偽 は 真
となる。
この内、3番目以外は納得できるだろうが、3番目を納得するのは難しい。
これを認めると、間違った前提から、どんな命題(主張)でも結論してよいことになる。
これは論理学が常識と大きく隔たる処で、古来、その意味が繰り返し議論されているが、
今でも解決できていない問題である。
以上の「規約」のもとで、but my baby loves only me 7、つまり、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
は、
Πi (-l5i+ (i = 7))
となる。つまり、数回前に行ったパズルの答えをパースの論理学でかけば、
Πi li5 Πi (-l5i+ (i = 7))
となる。これを英語風にかけば、
(For any person i. i loves my baby ) and
(For any person i. "my baby loves i" implies "i is me")
となる。
また、any person でなくて、anything にしたければ、次のようにする:
(For anything i." i is a person" implies "i loves my baby") and
(For anything i. "i is a person and my baby loves i " implies "i is me")