
尾崎の演繹推理学第三章のタイトルが名辞概論.
この名辞という概念が、もっとも重要なポイント。
名辞は英語では term。だから、これが重要となる論理なので、アリストテレス論理学のことを Term logic ともいう。
記号論理学も、西田の論理(哲学)も、名辞から述語に重点を移動させた。
つまり、これらの論理が乗り越えようとしたのは、この名辞という概念なのである。
そして、それは、この動画で言われている東洋人と西洋人のものの見方の違で、西洋的とされている「物」「対象物」のことだと思えば良い。(哲学的に言うと、ちょっと違っていて、実は名辞が何かには、哲学者により歴史上様々な異なる意見が出されている。しかし、ここでは、そういう難しいことは考えない!):
尾崎の教科書の10-11頁に次のような名辞の例が書かれている:
尾崎は,1のような名辞を「唯一個の人あるいは一個の事物を指言する者」と説明し,2のような名辞を「諸種の馬,諸国の王,諸方の府県会を指言する者」と説明し,それぞれ,
と名づけている.
そして,これら二つを合わせて
と名づけている.特称名辞は,一つの「者」しか表さないが,それでも何かが集まっているもの,ただし,ひとつしか集まってないもの,と考えるということ.
名辞と名詞を混同するという「方便」からすれば、
両方を合わせれば
というものが考えられるということになるが、文法用語では、集合名詞とは、information, furniture, software などの集合的に用いられ名詞。
集合名辞は、これとは違っていて、ひとつでもあり得る、が、集まりをあらわすもの。
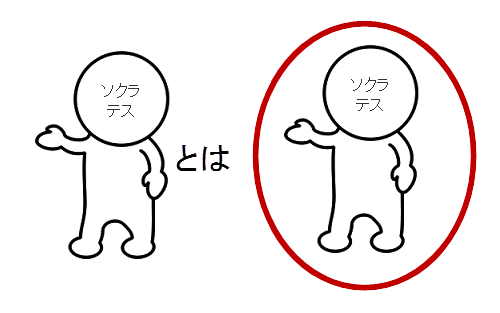
つまり、固有名詞も「集合」を表現している、たとえば、ソクラテスという固有名詞を特称名辞と理解したとき、それは我々が「ソクラテス」という言葉(固有名詞)で理解している、歴史上の人物ひとりからなる集合(数学でいう集合)と理解する。
これが、Term Logic の、非常に大きな特徴。
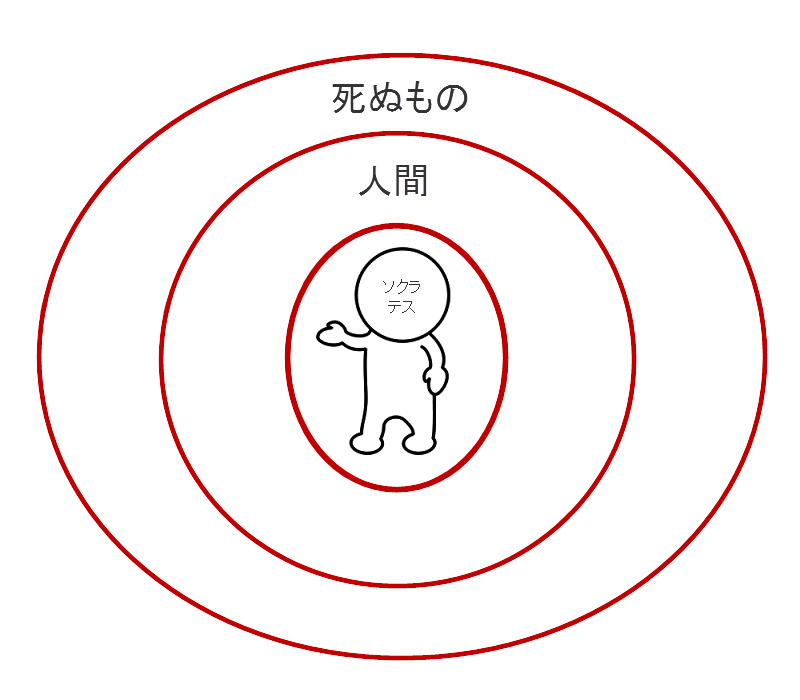
このようにすると「ソクラテスは人である」「人は死ぬものである」「ソクラテスは死ぬものである」 という,有名な三段論法にでてくる命題が,すべて同じ種類の連辞(英語なら is, are...)から,できるという,大きな長所がある.
しかし、これは単なる便利さの問題ではなくて、世界観の問題ともいえる。
実は、英語 term の元は、ラテン語の terminus、これが古代ギリシャ語では horos となる。
そして、この horos という言葉は、個々の対象物、物、Gegenstand と、それ以外を分け隔てる「境界」「壁」 boundary を意味していた。
このことへの違和感が西田の述語に向かう論理の大きな動機になっている。また、京都学派の哲学を貫く大きなモチーフになっている。
しかし、その話は後にすることにして、アリストテレス論理学入門を続ける。
尾崎は,以上の名辞の分類以外にも分類を示しているが,これからの話に直結しないので,それは略.次の章の命題の話に移る.
ここから尾崎の著書の第四章「命題概論」だ、ソクラテスが集合名辞だということの意味がわからなかったという質問票があったので、これを図を使って再度説明。この図が、今日の「命題概論」にも繋がる。








実はこの様に考えると、英語の
の様な文章と
が同じ種類の文章、あるいは、命題として考えることができる。
たとえば、
この様に考えると、有名な三段論法
の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ
の形であることがわかる。
これが尾崎の資料(本日の分)の18ページにある「合式命題」の説明。
アリストテレス論理学の命題論、つまり、項という「存在」(固有名辞)や「概念」(一般名辞)を組み合わせて「文」、それも「合理的で明瞭な意味」を表す文、いわゆる「命題」の作り方の基本は、この A be B という形。
日本語は、この形が基本ではないことに注意!
つまり、アリストテレス論理学というのは英語、ドイツ語、ギリシャ語などの欧州の言語の構造に強く根ざしている。
上で説明した尾崎がいう「合式命題」(この言葉は、ほとんど使われないので注意!)の形で世界を見ると、それは世界観に影響を与える、と京都学派の人たちは考えた。
しかし、この話は後回しにして、以上の説明を元に、尾崎の資料を見ていく。
片仮名漢字交じり文の中に、用例としての平仮名漢字交じり文が入っているので注意。しかも、合略仮名 コト(19頁1行目下から5文字目)を使ったり、同じ平仮名の異なる崩し字を使うなどしているので大変読みにくいが、言っていることは簡単:
ここまでは、上に虎の絵を使って説明したことと同じ。そして、次に新しいことが説明される。
命題は,この「―は―なり」の形だけではない.この形の命題は全称肯定命題と呼ばれるもの.命題は,全称v.s.特称,肯定v.s.否定の2つの対立軸を使い,全部で4種類考えられる.(21-22頁)
そして,尾崎は,図(ベン図)を使って,これを説明している.22頁の図
つまり、「すべて」(全称)とか「ある」(特称)のような言葉の要素が持つ意味も、二つの名辞のベン図の重なり具合で説明できると言っている。
「ソクラテスは死ぬべきものなり」は,ソクラテスという特称名辞をひとつしか指し示すものがない集合名辞だと考えると,1の全称肯定命題になることに注意.
尾崎の本で説明するのは,ここまでにして,以後は,Wikipediaの記事を使い,説明を行う.日本語の説明は良いのがないので英語.
上記4パターンを示す図 http://en.wikipedia.org/wiki/Square_of_opposition
黒い部分は、そこに要素がないこと。濃い赤の部分は、そこに少なくとも一つ要素があることを表している。
「命題とは二つの名辞の重なり具合を表すものだ」と考えてベン図の重なり具合を分類していみると、本質的には、この4つしかなくなることに注意!
左上のSaP では、 S be P の S の方だけ黒い領域があり、P の方に黒い領域がある場合が無いように見えるだろうが、これは S と P を交換すれば同じパターンになる。
右下の SoP も事情は同じ。
ちなみに、この図は、Square of oppoition と呼ばれ、この四種の命題の論理的関係、つまり、互いに矛盾しているとか、逆の命題であるとか、そういう関係を表したもの。
西洋の論理学者、哲学者は、この様な「二つの名辞の関係」で論理学を組み立てて、命題を分類し、さらには可能な推論をパターンで分類した。
それをシロギズムという。この話は凄くややこしいので、一部分だけ簡単に説明。
先ほどの三段論法の前提、つまり、1-3の内の、1と2
の状況を、今までのようなベン図で重ねて図示してみると
となる。あきらかに、
が分かる。つまり、有名な「ソクラテスは死ぬ」という三段論法は、数学でいう
つまり、
のことである。
これは
がどちらも全称肯定命題として理解されたとき、 A be B B be C の、中間の B をとって作った A be C という全称肯命題は、二つの前提が正しいときには正しいことを意味している。
同様のことを、1,2 と A be C のそれぞれを、全称肯定、全称否定、特称肯定、特称否定のすべてのパターンで考えて、その推論が正しいかどうかを、ひとつひとつ検討したもの。
図を見ただけでわかると思うが、兎に角、ややこしい…
で、その欠点を、「述語」の概念を取り入れることにより、解決したのが、数理論理学、記号論理学の体系である述語論理学。
次に、この話をするが、その前に、西田幾多郎の「述語的論理主義」をちょっとだけみる。
これでどうして前回、あのおもしろい動画を見たのかが明らかになる。
この二つのものは、どちらも「述語」と言っているが…