1章の補足資料: 現代的定義と covarinat という名称について ver.2025.02.17

1. 現代的な不変式の定義

この補足資料の主なテーマは、現代的な不変式論がどの様なものであるかを簡単に見ることである。「現代的不変式論」と書いたが、それは一つではなく、実は複数ある。しかも、そのスタイルは、Rota の皮肉ではないが、実にマチマチである。ここでは、それらの内、比較的、オリジナルな19世紀的不変式論に近くて、しかし、19世紀と、それ以後、つまり、20世紀以後の数学の違いが良くわかるものを紹介する。それは Hermann Weyl によるもので、群の表現論から不変式論を理解するという方法である。

1章で、[Kung&Rota1984]から次の一節を引用した。

Our language and notation are, wherever possible, patterned after nineteenth century usage. It might have been easier to adopt instead one of the many—too many, perhaps —equivalent languages that have been taking turns in the annual Paris display of mathematical fashion.

この後には、次の様な文が書かれていた。

One could, for example, rephrase the results in the language of representations of GL(2) over certain tensor spaces, or as the study of moduli parameterizing certain algebraic varieties.

これは、Paris のファッションに喩えた、現代的な不変式論のファッションの内、二つの代表的なものを引用したもので、最初の方が、これから紹介する群の表現論の言語を使うもので、2番目のものが、[Hilbert1893]を踏まえて、1960年代に David Mumford が創始した幾何学的不変式論というものを指している。後者の話は、このWeb文書では全く行わない。また、それはWeb文書の中心的テーマの有限基底定理とは、ほぼ関係がない。

以下では、この二つの内、群の表現論を使う Hermann Weyl による不変式の定義を、三つのスタイルで紹介する。第一のものは、1章の定義にできるだけ近づけた形、第二のものは林には一番バランスが良いと思われる[Sturmfels2008]での定義、そして、第三のものとして、Wikipedia の Invariant theory の記事でも、それが使われていると思われる、古典的と銘打ちながら、すごく Paris ファッション的な[Kraft&Procesi1996]のものである。

この三つの定義の紹介が、このセクション1の内容である。もう一つのセクションである、セクション2では、1章で説明した transform, transformation の使い方の変化のために、現代の数学者の間に誤解が生じているのではないかと思われることについて説明する。それは、covariant という専門用語の由来の話である。

1.1. 群の表現論を使う方法

現代的とは言うものの、これは1939年の[Weyl1939]で導入された方法である。ただ、1930年代になると、20世紀抽象数学の代表である、抽象代数学が整備されて代表的な教科書なども登場しており、Weyl 自身による集合論的位相幾何学を使った現代的なリーマン面、つまり、多様体の定義も登場しているなど、抽象数学というものが定着したという感がある時代なので、[Weyl1939]は今見ても、それほど違和感がない本である。ただ、この本は、多くの数学者が非常に読みにくい難しいと言っている本である。私は眺めたことはあるが、内容をちゃんと読んだことはない。

1章の不変式の定義の面倒というか分かりづらい所は、binary で言えば、binary ground form への2次元の線形変換の式の第入、つまり、ground form の変換を使って、その係数に関する別の三次元の線形変換を定義して、それで3変数の form が本質的に変わるか変わらないかで不変式を定義する所だと思う。1章で説明したように、これはほぼ偶然に生まれたアイデアなので、分かりづらくても仕方がないと言えば仕方がないのだが、Weyl は、この ground form を使った2次から3次への移行を、群の表現で抽象化して消してしまう。

実際に消えるわけではなく、古いものは、Weyl の定義の一例になっているわけだが、単なる一例にすることで、変な式の第入と式の整理を考えなくても良いよ、それは不変式論の本質ではないよ、という大数学者 Weyl からのメッセージをもらえた様な気がして、それで、気が楽になるのだと思う

実際にやってみよう。群は知っているものとする。また、一般線形群、特殊線形群も既知とする。知らない人は、Wikipedia などを参照しつつ読んで欲しい。

群の例としては、一般線形群、特殊線形群が有名だが、これは要するに正方行列とその積でできる群である。線形群は抽象的にベクトル空間上の線形写像が成す群という風に定義する方が Paris 的なのだろうが、このWeb文書は、そういう時代の前の話なので、そういう話が殆ど出てこないので、行列の話にする。一般線形群は2次元、3次元など各次元で定義できるわけだが、まず、2次の一般線形群 \(\mathsf{GL}_2\) を考えよう。これは正規な2次の正方行列、つまり、逆行列を持つ2次の正方行列の集合に、行列の積を、その集合上の積として定義される群であった。

つまり、これは1章の(2)の線形変換 \begin{equation}\tag{2} \begin{aligned} x_1 & = \alpha_{11}x_1'+ \alpha_{12}x_2', \\ x_2 & = \alpha_{21}x_1'+ \alpha_{22}x_2' \end{aligned} \end{equation} の群である。一般に、群が一つあるとき、その群から適当な一般線形群への群の準同型を、その群の表現 representation という。

ここまで書くと、気の早い人は、林は、1章の(4)の3次の線形変換 \begin{equation}\tag{4} \begin{aligned} a'_0 & = a_0\alpha_{11}^2+ 2a_1\alpha_{11}\alpha_{21}+a_2\alpha_{21}^2,\\ a'_1 & = a_0\alpha_{11}\alpha_{12}+ a_1(\alpha_{11}\alpha_{22}+\alpha_{12}\alpha_{21})+a_2\alpha_{21}\alpha_{22}, \\ a'_2 & = a_0\alpha_{12}^2+ 2a_1\alpha_{12}\alpha_{22}+a_2\alpha_{22}^2. \end{aligned} \end{equation} が、\(\mathsf{GL}_2\) の \(\mathsf{GL}_3\) による表現だというのではないかと思うかもしれないが、ホンの少し違ったものになる。

(4)を行列の積で書けば \begin{equation}\tag{5} \begin{bmatrix}a'_0\\a'_1\\a'_2\end{bmatrix} = \begin{bmatrix}\alpha_{11}^2& 2\alpha_{11}\alpha_{21}&\alpha_{21}^2\\ \alpha_{11}\alpha_{12}& \alpha_{11}\alpha_{22}+\alpha_{12}\alpha_{21} &\alpha_{21}\alpha_{22}\\ \alpha_{12}^2& 2\alpha_{12}\alpha_{22}&\alpha_{22}^2\end{bmatrix}\begin{bmatrix}a_0\\a_1\\a_2\end{bmatrix} \end{equation} である。つまり、 \begin{equation*}\tag{6} \rho\left(\begin{bmatrix} \alpha_{11} & \alpha_{12}\\ \alpha_{21} & \alpha_{22}\end{bmatrix}\right)=\begin{bmatrix}\alpha_{11}^2& 2\alpha_{11}\alpha_{21}&\alpha_{21}^2\\ \alpha_{11}\alpha_{12}& \alpha_{11}\alpha_{22}+\alpha_{12}\alpha_{21} &\alpha_{21}\alpha_{22}\\ \alpha_{12}^2& 2\alpha_{12}\alpha_{22}&\alpha_{22}^2\end{bmatrix} \end{equation*} という写像 \(\rho\) が定義できる。

これが準同型だといいのだが、計算してみると、この \(pi\) は、単位行列と、行列の積に対して、次の二つの性質を持つことが判る。 \[ \rho(E)=E,\quad \rho(AB)=\rho(B)\rho(A) \] このことから、\(A\) が正則ならば、\(\rho(A)\) も正則であることが分かり、少なくとも、これは \(\mathsf{GL}_2\) から \(\mathsf{GL}_3\) への写像であることがわかる。

しかし、2番目の式から、これは \(\mathsf{GL}_2\) から \(\mathsf{GL}_3\)　への準同型ではなく、\(\mathsf{GL}_2^\mathsf{op}\) から \(\mathsf{GL}_3\) への準同型だと分かる。ただし、\(\mathsf{GL}_n^\mathsf{op}\) は、 \(\mathsf{GL}_n\) の逆群、つまり、積の順番を逆にした群である。

纏めると、1章の(4)は、 \[ \rho: \mathsf{GL}_2^\mathsf{op}\rightarrow \mathsf{GL}_3. \] という表現であった。

\(\mathsf{GL}_2^\mathsf{op}\) を \(G\) と書くことにしよう。そうすると、binary quadratic の不変式の定義は次の様に書ける。

1章の定義１の言い換え： 3変数 \(a_0,a_1,a_2\) の form \(\mathcal{I}(a_0,a_1,a_2)\) に対して、ある非負整数 \(p\) が存在して、すべての \(g\in G\) と、\(a_0,a_1,a_2,a'_0,a'_1,a'_2\in\mathbb{C}\) に対して、 \[ \begin{bmatrix} a'_0\\a'_1\\a'_2 \end{bmatrix} = \rho(g) \begin{bmatrix} a_0\\a_1\\a_2 \end{bmatrix} \] ならば \[ \mathcal{I}(a'_0,a'_1,a'_2)=\delta^p \mathcal{I}(a_0,a_1,a_2). \] が成り立つ時、 \(\mathcal{I}(a_0,a_1,a_2)\)　を binary quadratic の不変式という。ただし、\(\delta\) は、行列 \(g\) の行列式である。

これは、1章の定義に近づけて書いたので、余計なものが入っているので、それをとりのぞくと、

1章の定義１の言い換え： 3変数 \(a_0,a_1,a_2\) の form \(\mathcal{I}(a_0,a_1,a_2)\) に対して、ある非負整数 \(p\) が存在して、すべての \(g\in G\) と、\(a_0,a_1,a_2,a'_0,a'_1,a'_2\in\mathbb{C}\) に対して、 \[ \begin{bmatrix} a'_0\\a'_1\\a'_2 \end{bmatrix} = \rho(g) \begin{bmatrix} a_0\\a_1\\a_2 \end{bmatrix} \] ならば \[ \mathcal{I}(a'_0,a'_1,a'_2)=\delta^p \mathcal{I}(a_0,a_1,a_2) \] が成り立つ時、 \(\mathcal{I}(a_0,a_1,a_2)\)　を binary quadratic の不変式という。ただし、\(\delta\) は、行列 \(g\) の行列式である。

これをさらに言い換えよう。

1章の定義１の言い換え2： 3変数 \(a_0,a_1,a_2\) の form \(\mathcal{I}(a_0,a_1,a_2)\) を考える。これは、\(\mathbb{C}^3\rightarrow \mathbb{C}\)の関数と考えることができる。また、\(\rho(g)\) も \(\mathbb{C}^3\rightarrow \mathbb{C}^3\)の関数と考えることができる。ある非負整数 \(p\) が存在して、すべての \(g\in G\) に対して、 \[ \mathcal{I}\circ\rho(g) =\delta^p \mathcal{I} \] が成り立つ時、 \(\mathcal{I}\)　を binary quadratic の不変式という。ただし、等号は、\(\mathbb{C}^3\rightarrow \mathbb{C}\)の関数として同じという等号、\(\circ\) は合成関数の記号であり、\(\delta\) は、行列 \(g\) の行列式である。

これで、19世紀的な定義では非常に沢山あった変数がほぼ消えてしまった。これが20世紀的スタイルというものである。Weyl は、\(\rho\) を、19世紀的に定義されるものから解放して、一般の表現でよいことにしてしまった。それでも不変式論の本質が変わらないからだろう。また、実際に、この様に定義するとき、上でやったように、逆群を考えるのではなく、定義式を \[ \mathcal{I}\circ\rho(g^{-1}) =\delta^p \mathcal{I} \] にすることが普通らしい。こうすると、\(\delta(g)=g^{-1}\) が、群とその逆群の同型なので、線形群の逆群を考える必要がなくなる。

20世紀現代数学では、座標とか、変数とか式とかの「表現形式」を非本質的なものと見做し、それから free であることが尊ばれたので、こういうことになる。そして、究極的には category になり変数が書けなくなってしまう。そのため変数や座標(の基)が写像に化けたりするわけだが、私などは、長年情報をやっておりプログラマでもあったので、変数がないとプログラムが書きづらくて大変だ、やり過ぎだ、と思ってしまう。category を使うプログラミングとか、プログラムの意味論とかいうのもあり実は後者は私も少し関わっていたが、category を使うプログラミングも、実際に書く時はやはり変数が欲しくなる。モノを中心に考えるのは、人間の本性ではないかと思う。

ところで、上の定義では、\(delta^p\) があって気持ちが悪い。そこで、一般線形群を止めて特殊線形群にして、これを常に1にしてしまうというのが現代流らしい。実際、そうしても、ほとんど変わらないのである。まず、特殊線形群は一般線形群の部分群なので、普通の不変式は、特殊線形群で定義した不変式になる。また、form で考えるのならば、特殊線形群で定義した不変式に、線形変換の行列式の逆数の、たとえば、binary の場合には、平方根でスケーリンング、つまり、スカラー倍すると、それは特殊線形群の行列になり、それに対する不変性の等式から、元の行列に対する不変性の等式が導かれる。ただし、不変式が form であると仮定しての話である。

この様なことから、現代では特殊線形群で考えることの方が普通の様である。また、表現の写像としての像は、当然、終域の群の部分群となるので、最初から、それで考えるという流儀もあり、これが一番簡単でスッキリしている。[Sturmfels2008]のp.14の不変式の定義はそうなっていて、そうすると、不変式の定義は、n変数の多項式の、n次の特殊線形群のある部分群に対して、上のような合成関数による作用したとき、それの不動点が不変式ということになる。おそらく、この Sturmfels が使っている定義が、一番シンプルな定義だと思うが、勿論、それで19世紀定義では考えられたものが幾つも落ちてしまうはずだが、私は専門家でないので分からないが、それでも不変式論の本質が変わらないと数学者たちが判断したので、そうなっているんだろうと思う。この変化の過程を明らかにするというのは、数学史の問題としてなかなか面白いと思うが、不変式論の文献は多いので、随分大変な作業になりそうでもある。

最後に、私が見た範囲でももっと Paris fashion 的な classical invariant theory の invariant の定義を紹介して、この話を終わろう。それは、[Kraft&Procesi1996]の定義で、それを reproduction する。

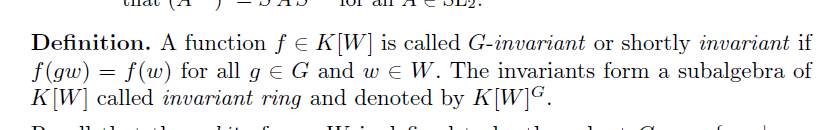
この定義にでてくる \(K[W]\) は、ベクトル空間上の体\(K\)の係数の多項式環というもので、次の様に定義される。

最初にこれを見た時には、ここまで「表現形式」を消し去りたいのかと唖然としたが、読者はどう感じるだろうか？

ここで東大講義で出したエキストラの宿題の問題をパズルとして出しておく。\(\rho\) が2次の一般線形群の逆群から3次の一般線形群への準同型であることは計算で簡単にわかるが、では一般の場合はどうやったら証明できるだろうか。これを19世紀の人でもできるように、行列も線形写像も使わず、1章の様な一次式の第入だけで考えてもできる方法で証明を試みて欲しい。ヒントは「代入は色々な式の操作と交換可能」である。

2. Covariant は、どうして co なのか

このWeb文書では、説明していないが、19世紀の不変式論では、covariant とともに contravariant という言葉が良く使われていた。co- contra- は共変ベクトル、反変ベクトルというときにも使う。実は、covariant vector, contravariant vector と不変式論の covariant, contravariant は語源が同じで、Sylvester の論文[Sylvester1851]なのである。こちらのPDFファイルの289頁からが、それである。その290頁の最後のパラグラフに、covariant, contravariant などの定義がある。そして、考えている linear tranformation と同じ変化なら co-, 逆変換と同じ変化なら contra- と呼ぼうとしている。

現代の数学者が書いたものをみると、covariant は、本当は、contravariant ではないのか、という感想が書かれていることがある。たとえば、Olver の本のpp.64-65の Remark がそうである。Olver は "perhaps perversely, although we are adhering to the classical terminology", 「おそらく逆だとおもうが、古い用語に従うことにする」と書いている。これの原因は、もちろん、1章で説明した transformation, tranform の「向き」の、現代と19世紀における逆転である。おそらく、Olver は、この用語の違いに気が付いてないのだろう。

また、[Hilbert1993]の Sturmfels による Introduction のxページでは、Hilbert の covariant の定義に、contragredient representation (inverse representation) が使われていると注意しており、これを忘れると、'Otherwise the whole concept of "covariant" does not make sense.' と書いている。こちらの方は、1章で行った私の注意と同じ事を、現代の言葉で行っているわけである。Sturmfels の著書[Sturmfels2008]は、現代的な用語で書かれているが、基本は[Kung&Rota1984]に基づいてると宣言してあるので、Sturmfels はちゃんと気が付いていると思われる。ちなみに、[Kung&Rota1984]は19世紀のパターンに従うと書いてはあるが、transformation のイメージが現代と逆だというような数学史的な説明はないので、[Kung&Rota1984]を読んだ事がある人でも、これに気が付いていない人は少なくないと思われる。

興味がある人は、上の Sylvester の論文を読んでみて欲しい。逆行列の逆行列は元の行列ですので、ある行列とその逆行列の関係は「相互的］reciprocal だが、まだ、行列という概念ができていない時代であるため、ある行列とその逆行列の関係を、「逆行列」という言葉で書けず、簡単に言えばクラメールの公式を使って表現しているなど、古風な所が大変面白い。Sylvester の文体は、Cayley などに比べても大分古風であるらしく(Boole は議論の仕方は滅茶苦茶だが文章は割と現代に近い)、読むのに苦労すると思うが、それがまた歴史学の醍醐味である。

実は、東大の講義では、この Sylvester の論文を使う宿題を考えていたのだが、英語が難しすぎるかもしれないと考え断念した。京大文学部で歴史系の2回生の英書購読を担当した時、米国の historiography (歴史学の歴史学)の凄く良い本を見つけたので、それを使ったら、平文は考えていた通り、格調高いものの読みやすい英語で問題なかったが、古い時代の文献の引用が、この講義の資料での引用以上に沢山入っていて、学生たちがそれを読めず、特に難しい所は私が資料に補足のメモを入れるなどせねばならず大変だったのを思い出したからである。

ちなみに、その本の題名は、"That Noble Dream" である。アメリカの歴史学会の賞を授けられた本で、歴史学が好きならば、最初の方の19世紀までの話は絶対読んだ方が良い様な名著だ。私の歴史好きは、中学生の頃からだが、立教大学の数学科にいたときは、立教は特別数学史の講義が多かったのだが、数学史の講義には全部出ていた。もしも、読者の中にも、そんな風な人がいたら、是非読むことをすすめる。面白いですよ。何だか Boole みたいに話が変わって来てしまった所で、これで補足資料を終わる。