来年度、情報・史料学に配属された人は質問票を提出したら、林の所に来てください。5分ほど「ガイダンス」をします。
Everybody loves my baby,
But my baby don't love nobody but me.
から、my baby is me. という結論が推論(演繹)できる理由。
注:演繹と推論の違いは?昔は、これがハッキリと分けられていたのですが、今の記号論理学では混同して用いられます。多分、「論理学にあるのは演繹のみで、推論 inference などない」と主張したラッセルの影響でしょう。
Pierce 流に書くと、分かりやすいので、それで推論しましょう。
これをパースの論理学で書くと、
Πi li5 ×Πi (-l5i+ (i = 7))
でした。5が my baby で、7が me です。
掛け算×は、「かつ」だったので、
Πi li5
が成り立ち、Πi … は、「すべてのi に対して、…が成り立つ」ことだったので、i に5を代入すると、l55になります。
同様に、
Πi (-l5i+ (i = 7))
のi に 5 を代入して、
-l55+ (5= 7)
になります。
これは、 -l55 か 5= 7 のどちらか、少なくとも一方は正しいということですが、l55 が正しいので、 -l55は偽です。ということは、5=7が正しくないといけないことになり、つまり、my baby is me、ということになります。
ポイントは、l55、つまり、「my baby は my baby を愛している」という変な命題を演繹することです。日常言語では、Everybody loves my baby. の everybody には、my baby は入りません。そういうのは「暗黙の了解」とでも言うべきものですが、条件を杓子定規にとると、こういう変なことが起きます。
パースの論理学や、それに関連した論理学から進歩した現代の論理学の代表は、述語論理学。より正確には第一階述語論理学という。
これを簡単に説明してアリストテレス論理学との相違を説明する。アリストテレス論理学と述語論理学では、同じ用語が違うものを表しているので混乱しないように注意。
アリストテレス論理学の singular term、たとえば、「ソクラテス」に対応するもの。
ただし、terminus (境界、柵)は考えず、その中にある丁度一つの個体を表していると考える。
アリストテレス論理学で、ソクラテスという対象、個体を表す名辞を考えて、
それを So、人間の全体を表す名辞を考えて、それをHu とすると、
「ソクラテスは人間である」が、
So be Hu
と書けた。図にすると

アリストテレス論理学の名辞を数学の集合だと考えれば、
So be Hu
とは、
So ⊆ Hu
のこと、つまり、
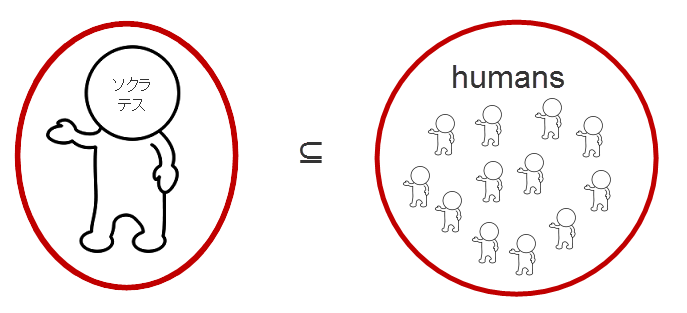
ということ。
述語論理では、これを、ソクラテスの terminus を取り払って、数学の集合論で 9∈{1,3,5,7,9...} とするように、
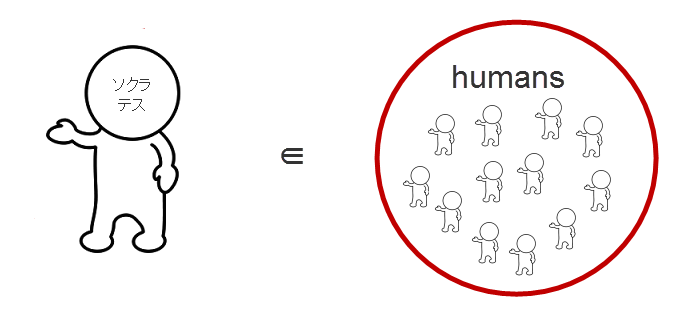
と考える。

ではなくて、柵なしの個

を表す定数記号を so とすると、
So ⊆ Hu
ではなくて、
so ∈ Hu
と考えるということ。
この so を、述語論理学では、term と呼ぶ。
アリストテレス論理学の場合の term は、名辞と和訳されていて、だから、名辞論理学という日本語があるのだが、述語論理学の場合の term は、項と訳される。これは、多項式というような時の、数学の項という用語(英語ではterm)から来ていると思われる。
上の例では、so ∈ Hu と書いたが、述語論理学では、集合の∈は使わないで、述語記号というものを考えて、これを数学の関数のように書く。
具体的にいうと、 Humans という集合にあたる述語記号 Hum を考えて、
so ∈ Hu
を、
Hum(so)
と書く。
この関数の書き方 f(x) に似た書き方が便利なのは、f(x,y) の様な二変数の関数のようなものが使える点。
たとえば、i loves j は、パースでは、
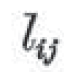
だった。これは2変数の数列のような記号だが、数列というのは、この Wikipedia の数列の記事にあるように、実は関数、
この場合では2変数関数のことだから、Loves という2変数の述語記号を考えて
Loves(i,j)
と書く。これは、下付きの添え字を使わないで済むので、パースの記号より楽。
この様な、多変数の述語を使えるところが、述語論理の優れた点であるが、1変数の述語、たとえば、Hum は、アリストテレス論理学の名辞、つまり、term である Hu に対応している点に注意しなくてはいけない。
一般に、Loves(i,j)のような多変数の述語は、i,j の対、あるいは、タプル [i,j]を考えれば、Lo([i,j])という1変数の述語と見なすことができる。
つまり、Lo とは、「 i loves j であるようなタプル [i,j]」という名辞である。
これを考えると、次のような対応になっていることが分かる
| 伝統論理学 | 名辞 (term) | なし |
| 述語論理学 | 述語 | 項 (term) |
10月24日の資料で名前がでてきた、イギリスの哲学者バートランド・ラッセルは、現代的数理論理学の成立に非常に大きな役割をした人である。
そのラッセルの1903年の著書 The Principles of Mathematics は、後の著作 Principia Mathematica とともに、現代的記号論理学や述語論理学の成立への重要なマイルストーンである。
ラッセルは、この著作では、まだ、term を、伝統論理学、つまり、名辞論理学と同じ意味で使っている。ラッセルが、この著書で、名辞論理学に対して、どういっているかを見てみよう。
ラッセルは、この本で、class と class-concept という言葉で、集合と集合の定義を区別した。クラス class というのは、このころ物の集まりに対して使われていた言葉。現代的に言えば、集合だと思えばよい。
たとえば、先に見た、ケインズの論理学の教科書でも、唯の集まりを表す用語として、class が使われている。
一方で、class-concept というのは、そういうクラスを定義するときに使われる概念という感じ。
たとえば、
{2 4 6 8 10} と {x|x は10以下の偶数}
は同じクラス(集合)だが、右の「x は10以下の偶数」が、class-concept。
つまり、高校で習う、外延的定義と内包的定義の、内包的定義の方で、定義するために使われるものが class-concept だと思えばよい。
伝統的論理学が、ほぼ、現在のような形なったといわれるのは、1662年にフランスのポールロワイヤル修道院で書かれた通称「ポールロワイヤル論理学」という本からである。こちらが英訳。
そのポールロワイヤル論理学には、外延 extension (extent ともいう)、内包 intension という言葉があり(もとの本では、intension ではなく comprehension という用語だが、現代的な用語で書く)、内包は、Termが本来持つべき属性で、それが無くなると、もう、そのTermであらわされるものにならないようなもの、つまり、Termの本質のようなものとされた。一方で、外延は、そのTerm、あるいは、Termの内包が表すもの全部を集めたものとされていた。
たとえば、ポールロワイヤル論理学では、直角三角形という Term の内包には、その外延、図形、三つの辺、三つの角、直角三角形の法則、などが含まれると説明されている。
そして、内包の属性の一つとされた外延とは、そういう内包をすべて所有する、個々の直角三角形の集合のことである。
つまり、いままで、Term を集合として説明してきたが、正確に言うと、これは Term 名辞の外延である。また、ある名辞の外延は、その名辞が本質的に持つものなので、これも内包に含まれるとされる。
名辞論理学では、内包の方が外延より本質的であるとされるが、実は、内包というものは、よくわからないものでもある。それに比べると、外延の方が、すっきりわかりやすい。
この哲学的な内包概念をやめて、最初から、外延で論理を作り直したものが、数学の集合論や記号論理学だともいえる。
しかし、そういう集合としての Term を定義するさいには、やはり、{x|x は10以下の偶数} の赤字の部分のようなものが必要なので、ラッセルは、ここにだけ intension を、残して、これを class-concept と呼んだ。おそらくは、それが継承されて、高校で教えられるような、外延的定義、内包的定義という用語が生まれたと思われる。
ラッセルのThe Principles of Mathematicsでは、名辞としての Term の内包にあたるものは、このように class の「定義」にだけ使われるものに限定されるようになり、class、集合、外延と並置されるようなものではなくなっている。これにより、ラッセルは、内包にまつわる哲学的曖昧を避けることに成功している。
それにも関わらず、この1903年の本では、Term という英語は、まだ、伝統的論理学の名辞の意味として使われ続けており、また、伝統的論理学と、彼の新アプローチの違いが、いろいろと議論されるために、伝統的論理学的な議論が多くみられる。
それをいくつか紹介:
セクション21で、ラッセルは、新しい論理学では、「ソクラテスは人間である」を、So ⊆ Hu ではなくて、so ∈ Hu と理解することを説明した。
古い論理学(名辞論理学)では、A⊆BとA∈Bが同じ categorical propositon として混同されて理解されている。このことを指摘したのが、イタリアのペアノで、この指摘が大変重要である、とラッセルは主張した。」
セクション43では、もともと、命題の基本である categorical proposiotn を subject, copula, predicate で考えたのがおかしい。 動詞を無視している、とラッセルは主張し、
"Socrates is a man" は、 Socrates | is | a man ではなく、 Socrates | is a man と分割すべきで、is a man という一塊が、述語という存在になるのだ、とした。
第4章では、伝統的論理学の名辞についての詳しい議論が行われている。その Chap.IV の題名は、Chap. IV: Proper names, adjectives and verbs.
記号論理学では、こういう日常言語の文法について議論は行われない。これは、1903年の時点のラッセルの記号論理学が、まだまだ名辞論理学とのつながりを残していることを示している。
その4章のセクション46の内容は、目次では、§46. Proper names, adjectives and verbs distinguished と説明されている(この本は、古い形式で書かれていて、本文中の各セクションには、題名がない。
そして、目次 TABLE OF CONTENTS のセクションのリストには、現代ならば、セクションの題名に対応するものが書かれている。
だから、ラッセルがセクション46で主張したことは、固有名詞 proper name, 形容詞 adjective、そして、動詞 verb が区別されなくてはいけない、ということ。
名辞論理学では、これらが、すべて同じ名辞 Term だった。形容詞については、説明していないが、「赤いもの」という名辞が red という形容詞に対応すると考えて、The apple is red. という文を categorical proposition であるとするということ。
また、セクション47は、目次では、Terms という題名がついていて、ここで、 Whatever may be an object of thought, or may occur in any true or false proposition, or can be counted as one, I call a term. This, then, is the widest word in the philosophical vocabulary. と、Term を説明している。これは、名辞論理学の term と本質的に変わりがない。
しかし、ラッセルは、セクション48で、その Term には、実は二種類あるとする。次が原文
Among terms, it is possible to distinguish two kinds, which I shall call respectively things and concepts.
The former are the terms indicated by proper names, the latter those indicated by all other words.
つまり、ここで、はっきりと、ソクラテスのような固有名詞が表す Term と、人間の様な一般名詞が表す Term を区別し、前者を thing 物、後者を concept と呼ぶ。
そして、後の述語論理学では、この thing を表すものが term と呼ばれるようになり、concept は、述語 predicate と呼ばれるようになったわけである。
現代の述語論理学や、その源流のラッセルの1903年の論理学で、term がどのように扱われるかを確認したところで、述語論理学の term の話は、終わりにして、述語論理学の他の部分の説明を続ける。
パースの論理学では、
Π、Σ、掛け算、足し算、マイナス記号がつかわれていたが、述語論理では、これらの代わりに∀,∃,∧,∨,¬
の五つの記号使う。∀,∃ は全称記号、存在記号と呼ばれる。高校の数学にも出てくるらしいが、全称記号は、顔文字に使われるので見たことがある筈。(・∀・)
そして、以上の記号を使って、パースの「数式」
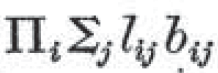
は、i loves j の述語記号を Loves、そして、i benefits j の述語記号を Bnf とすると、
∀i.∃j.(Loves(i,j)∧Bnf(i,j))
と書ける。こういう式を論理式という。論理式では、この例にあるように、部分の式を表すために、数式と同じく括弧をつかう。また、∀i.∃j.の様に、全称記号、存在記号を使うときには、その後の変数 i, j の後に、ピリオドを書くことが多い。
「人は皆死ぬものなり」は,「死すもの」の項 Mo を考えれば,
Hu be Mo
だが,これの全称肯定は、
∀x.(Hum(x) →Mor(x))
と書ける。ただし,Mor は,Mo に対応する述語記号,つまり,Mor(x) は x is mortal を表す。
また、
○→×
は、パースのところでやったのと同じで、
¬○∨×
のこと。
同様に、特称肯定は、
∃x.(Hum(x)∧ Mor(x))
全称否定は
∀x.(Hum(x) →¬Mor(x))
特称否定は、
∃x.(Hum(x)∧¬ Mor(x))
と書ける。
つまり、述語論理学は、アリストテレス論理学の命題で記述できるものを全部記述できる。
詳しいことは省くが、述語論理では、三段論法のように、前提から結論を導く方法を、論理記号についての形式的・機械的な「推論の法則」で説明できるようになっている。たとえば、「ソクラテスは人である」 の表現 Hum(so) と、「すべての人間は死ぬ」の表現 ∀x.(Hum(x) → Mor(x)) から、「ソクラテスは死ぬ」の表現 Mor(so) を導くには、次のようにする。
表現力については、アリストテレス論理学に、述語論理学では表せないものがあるとされることがあるが、実は、これは微妙な結論である。
述語論理やパースの論理学には、∀x や Πi の x や i の様に、数学で使われる変数が使われている。日常言語と関連が深い、アリストテレス論理学には、そういう数学の変数のようなものがない。実は、アリストテレス論理学でも変数の使用を認め、それにより {x| x は2で割り切れる整数} というように偶数の集合を定義するように、変数を使って、自由に名辞を定義してよいことにすると、categorical proposition だけでも、述語論理と同じ表現力をもつようにできる。
しかし、日常言語が貼り付いていたといえる、アリストテレス論理学は、my baby is me の推論の様な、日常の言語の感覚からは不自然なものは避ける傾向があり、これが、色々な制限をもたらしていた。述語論理学やパースの論理学は、数学を使うことにより、その日常性を無効にすることにより、表現力を増したとも言える。
なぜ、このように失われたのか、失われても記号論理学はアリストテレス論理学を「駆逐」できたのか?この疑問への解答を、最初に見たラッセルのインタビューを元に考える。
“the longing for love, the search for knowledge, and unbearable pity for the suffering of mankind.”
バートランド・ラッセルの三つの情熱:
愛への渇望、知識の探究、そして、人々の悲惨への耐え難い感情(pity)
インタビュワー:
Have you found on the whole in your own life, that the pursuit of either mathematics or philosophy, has given you some sort of substitute for religious emotion? (最初から11分25秒の辺りにあります)
数学や哲学は、あなたにとって、宗教的感情の代替物ではありませんでしたか?
ラッセル:
Yes...it certainly did...I mean uh..oh well, until I was about...40, I should think. I got a sort of satisfaction that Plato says you can get out of mathematics.
It was an eternal world.
It was a timeless world.
It was a world, where there was a possibility of a certain kind of perfection.
And I certainly got something analogous to religeous satisfaction out of it.
ええ…そうです。実際…ああ。40歳のころまでは… (略)
述語論理学やパースの論理学には、何ら宗教的、哲学的なものは見られなかった。
何故、ラッセルは、そんなものをキリスト教的宗教の代替物にすることが出来たのだろうか?
彼が宗教の代替物と感じたのは、論理学だけから数学を基礎づける可能性。
もっと具体的に言えば、自然数、整数、有理数、実数、複素数などの数を、論理学だけをもとに再創造する可能性。
30歳の頃のラッセル(ラッセルの生誕と没:1872-1970)は、これを成し遂げたと信じていた。
その時の様子は、彼の自伝に詳しい。毎日が、数学というプラトンのイデアの世界を、自分が論理学という「すべての学問に先立つ基礎的学問」のみを使い再創造しているという知的恍惚感で満たされていた。
つまり、ラッセルにとって、数学の世界は、eternal 永遠不滅で、timeless 時間を超越し、there was a possibility of a certain kind of perfection ある種の完全なる理想が可能な世界だった。
次は、その話。
今までの話では、記号論理学、述語論理学を、哲学の一部であったアリストテレス論理学の視点から見て説明を加えてきた。
記号論理学が得たものの話の所で注意したように、アリストテレス論理学は日常言語の文章を論理的に表すものであり、数学の変数の様なものがそれに入ることは不自然であった。つまり、本来は、哲学の一部であった、アリストテレス論理学は、言ってみれば「文系」であった。これに反して、変数を躊躇なく使う記号論理学は、数学をモデルとしており、「理系」であった。
ラッセルは、1903年の The Principles of Mathematics では、アリストテレス論理学の教科書に出てきそうな、日常言語の例を数多く用い、今から見れば不思議な議論を延々と行なっており、まだ、アリストテレス論理学的なものを引きずっていることが見て取れる。
しかし、ラッセルの記号論理学の本当の目的は、そういう「アリストテレス論理学の代替物、あるいは、進化形を作ること」ではなく、「数学を基礎づけること」であった。
19世紀には、数多くの「新しい数」や「新しい空間」が発明されるなど、数式の学問だった数学に様々な新概念が導入された。これらの技術革新とともに、実数や無限小などの、近世以来使われ続けていた数学の概念の基礎を、よりクリアにする必要性が生まれた。たとえば、実数、特に無理数とは何なのか、そもそもそれは存在するのか、そういうことについて議論が行われた。ラッセルがしようとしたことは、この数学という学問の基礎付けを once and for all で解決してしまうことだった。
ラッセルは、一度、それを成し遂げたと信じ、数学はプラトンのイデアの世界を代表するものであったこともあって、宗教的とさえ言ってよい陶酔に浸ったが、数年後、それは一挙に悪夢に暗転する。そして、長い苦闘が始まり、その努力は、彼の代表作、Principia Mathematica 3巻に結実する。その第3巻が出版されたのが、彼が40歳の時だった。そしてのインタビューでの彼の答えからすれば、その後、彼は、それに宗教に代わるような意味を見出さなくなる。そして、その後に残されたものが、現代の記号論理学であった。しばらく、このラッセルのストーリー。
そのストーリーは、歴史上もっとも華やかだったともいわれる1900年の万国博覧会に沸く、パリの暑い夏に始まった。
この時代の万博は、ベルエポックと呼ばれる西欧列強の反映の時代における、西欧の経済力・科学技術力のショーケースだった。そして、万博のアトラクションとしてオリンピックや、様々な学術分野の国際会議が開催された。そんな国際会議の一つが、第1回国際哲学会議であった。それに参加した28歳の若きラッセルは、ある衝撃的なものに出会う。それがパースの論理学を継承・発展させていた、イタリア、トリノ大学の数学者ペアノの論理学だった。
その出会いを、ラッセルの自伝にみる:
p.148, 3行目の The time was one of intellectual intoxication それは陶酔の時であった、という表現に注目。これこそが、彼に宗教的感情の代替物を与えたものだった。
その前後を和訳:
毎夜、(Whitehead との)議論は何かの困難にぶつかって終ることとなった。しかし、翌朝には、常に、問題は解けていた。私の睡眠中に問題が自ずと解けていたのである。それは知的陶酔の時であった。私がその時感じた感覚は、霧の中を登山し、頂上に到達したとたんに、すべての霧が晴れて、360度すべての方角の田園が40マイル(64km)先まではっきりと見て取れる、丁度、そんな感覚だった。
彼が成し遂げたことは、1903年に出版されたThe Principles of Mathematicsで、次のように説明されている。
ラッセルが主張したのは、数学のすべての概念、自然数とか、実数とか、複素数とか、幾何学空間、微分積分、あるいは、それらより遥かに高度な専門的概念がすべて記号論理学の言葉だけで定義できて、しかも、それらについての定理が、すべて、わずか20個の前提(公理)から論理推論だけで証明できるということ。
つまり、数学を完全に書ききることを可能にする言語と真理の素のようなものを、 わずかなページ数で書ききることができるということ。
ある種の人たちは、これを「世界を掌の上においた」ように感じる。林も若いころには持っていた、世界を全部記述したい、全部理解したい、という emotion。
そして、ラッセルは、それを自分が実現できたと信じた。
ラッセルが、全数学を乗せた掌を、現代的に書けば、
で済む。ただし、クラス(Class)というのは、ラッセルや、その時代の論理学の教科書、例えば、以前紹介したケインズの論理学の教科書で、「ものの集まり」を表すために使われた用語で、現代の集合 Set と同じ意味だと思えばよい。
特に5の内で重要だったのが、内包の公理と呼ばれるもので、
F[x] が論理式ならば、
∃a.(Class(a)∧∀x (F[x] <-> Belong(x,a)))
と書かれるもの。ただし、 A<->B とは、 A->B ∧ B->A を省略して書いたもの。
これを日本語で書けば、
あるクラス a があって、それは、F[x] という条件を満たすもの全部からできている。
ということ。
これは言葉(論理式)で表せるものは通称名辞としてよいと言っているのと変わらないから正しそうに見える。
また、クラスは、数学でならう集合と同じと思ってい良いので、
Belong(a,b) は、数学で a∈b と書く、おなじみにもの。
また、内包の公理が、その存在を主張するクラス a は、普通の数学で、{x | F(x)}と書くもの。
つまり、区間 (0,1) を、{x | 0<x<1}と定義したりときに使う記号が書かれる集合が存在するということを主張している。
高校までの数学では、そういう集合があるというのは、当たりまえのこととして使っているが、
この axiom of comprehension (包括の公理)と呼ばれるものは、そういう、クラス、集合の存在を、わざわざ保証しているもの。
そして、ラッセルは、この「当たりまえ」の公理が保証する eternal で timeless なクラス、集合という存在のみから全数学を再構築することに成功した。
たとえば自然数の1を作ってみよう。
ラッセルは、自然数1を, 特称名辞のように、対象が一つしか入ってないクラスすべてのクラスとして定義した。
クラスaに要素がちょうど一つしかないということは、there is only one element in a. ということだから、my baby loves only me と同じ要領で、
∃x.(x∈a)∧∀x.∀y.(x∈a∧y∈a→x=y)
と書ける。
だから、数1というのは、「要素が、ちょうど一つしかないクラスの全体」として、
{a| Class(a)∧∃x.(x∈a)∧∀x.∀y.(x∈a∧y∈a→x=y)}
というクラスとして定義できる。
注。このクラスをOneと書くと、s が入っている対象がひとつのクラスであることが、s∈One と書ける。
同じテクニックで、2は入っている対象の数数が丁度二つのクラスを全部集めたクラスとして、3は三つ入っているクラス全部のクラスのように定義できる。
大変、手間はかかるが、このようにして、整数、有理数、実数、複素数などすべての数作っていくことができる。
そして、数の世界を創造すると、それを利用した幾何の空間も創造することができる。(座標を使う)
そしてラッセルが、The Principles of Mathematics?、§ 4に書いたように、これから生まれてくるだろう数学の概念も、この仕組みだけを使って作れるだろうという、確かな手ごたえがあった。
それは、まさに、 a certain kind of perfection だったのである。