アリストテレス論理学は、実に長い間、西洋では思考の基本様態、あるいは、それに近いものとして考えられていた。しかし、それを、本当の推論に適用しようとすると、実は、シロギズムの説明でみたように、実にややこしい。
実は、それだけでなくて、普通の日常生活で使う文章を、たとえ、S be P を基本とする英語の場合でも、アリストテレス論理学の形式で表現しようとすると、色々と困難にぶつかる。特に、それは、人と人との関係性、ものとものとの関係性などの「関係」を表現しようとすると、大変に不自然な表現になることがわかる。
たとえば、下のジャズ Everybody loves my baby. の歌詞の赤字の部分を、S be P で記述してみよう。
歌詞:http://www.youtube.com/watch?v=V42uJKhoe2I
I'm as happy as a King,
Feelin' good n' everything
I'm just like a bird in Spring,
Got to let it out.
It's my sweetie, can't you guess?
Wild about her, I'll confess!
Does she love me?
Oh my, yes!
That's just why I shout:
Everybody loves my baby,
But my baby don't love nobody but me.
Nobody but me.
Everybody wants my baby,
But my baby don't want nobody but me
That's plain to see.
以下略
つまり、次の二つの文章を S be P にする。
(but が消えて、カンマがピリオドになっているが、こういうものは論理的内容には影響を与えないと考える。)
1. Everybody loves my baby,
2. But my baby don't love nobody but me.
の1は、
all persons are "my baby"-lovers.
と書ける。
2は、内容的には、次の二つの文章と同じ。
2.1. my baby don't love anybody who is not me.
2.2. my baby loves me
2.2 は、1と同じテクニックを使って、
my baby is a me-lover.
2.1 は全称否定にすればよさそうなので、
my baby is non-P
だろうと推測できる。元の英文と比べて考えると
my baby is non-((anyone who is not me)-lover).
となる。ちょっと言い方を変えて
my baby is non-((non-me)-lover).
この様に、A loves B などのような、二者、あるいは、それ以上の者の関係をアリストテレス論理学で表そうとすると非常に不自然なことになることが多い。
その直観的理由としては、アリストテレス論理学が、個を出発点として、その terminus による分類で世界を記述しようとするからである。
このことを、たとえば、ドイツの哲学者、エルンスト・カッシーラーは、その著書「実体概念と関数概念」で、もともとが動物学のような分類科学をモデルにしてアリストテレス論理学が作られているからだと書いた。
これに対して、全く違う観点、動物学のような分類学ではなくて、数学をモデルにして論理学を再構成した人たちがいた。それがラッセルたち初期の記号論理学者。
ここでは、ラッセルをさらに遡り、その源流の一つとなった、アメリカの哲学者パースの論理学と、さらに、その元になった、イギリスの論理学者ブールの論理学を見ていく。
パースの論理学には、三つのポイントがあった。それは
まず、この第1のものから見よう。
A loves B
のような二つのもの関係を記述するとき、
A is a lover of B
でなくて、
A loves B
と書ければ随分楽。
他の例
A benefits B
A is a benefactor of B
パースは、このような二つのもの関係を記述するとき、
i loves j
i benefits j
を、数学の記号を使って、それぞれ
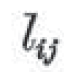
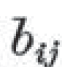
と書いた。
今ならば
L(i,j)
B(i,j)
と書く。
注. パースの例は、トマス・アクィナスの論理的問答集「神学大全」における「施し」「恩」についての論理的・哲学的・神学的議論を意識していた可能性が高い。トマス・アクィナス「神学大全」 Summa Theologica より (vol.3,part2.sec.2)。Twelfth Ariticle の内容は Whether a Man Ought to Love More His Benefactor Than One He Has Benefited?「人は施したるものより、施しを受けしものを、より愛すべきや?」http://books.google.co.jp/books?id=A7Cf9Bt1DWsC&pg=PA1297&dq=benefactor+lover&hl=en&sa=X&ei=22eVUvDaLcb5kAXe54DIBg&ved=0CEQQ6AEwBA#v=onepage&q&f=false
この様な述語の記号(述語記号)を導入すると、たとえば、
「全ての者は、誰かを愛しており、また、その者に施しをなす」
あるいは
「全ての者は、誰かを愛しており、また、その者に恩をなす」
が、
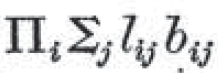
と書ける。
では、このΠとか∑は何か?
これが quanifier 量化子と呼ばれるもので、これがパースの、もう一つの大発明。
(フレーゲと)パースが行った述語の導入は、数学の関数
f(i,j)
や数列
aij
のような記法にならったもの。
パースは、さらに数学の記法を論理学に応用した。
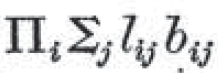
の
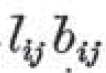
の部分は、 lij と bij の掛け算を意味している。
これは、1を真、0を偽と考えて、
1×1=1
1×0=0
0×1=0
0×0=0
となるが、これは
真かつ真 は 真
真かつ偽 は 偽
偽かつ真 は 偽
偽かつ偽 は 偽
という「かつ」の真偽の規則と一致する。
+の方は
1+1=2
1+0=1
0+1=1
0+0=0
となるが、2は1以上なので、1とみなすと、
1+1=1
1+0=1
0+1=1
0+0=0
となり、これは
真または真 は 真
真または偽 は 真
偽または真 は 真
偽または偽 は 偽
という、数学でつかわれる「または」と一致する。
さらに、マイナスを否定とみなして、
-0=1
-1=0
と定義すると、ドモルガンの法則などが成り立つ。
-(A + B) =(-A)×(-B)
-(A×B) =(-A)+(-B)
このように演算を定義した0と1の代数はブール代数と呼ばれるものの一つの例で、イギリスの数学者ジョージ・ブールが発明した。
パースは、このブールの考えをさらに発展させて量化子を論理学に導入した。
たとえば、前に考えた例
Everybody loves my baby.
を考えてみよう。これは、
All persons love my baby.
のことである。そこで、数学の変数(あるいは添え字) i が人間、つまり、persons を表すとする。すると、この文章は、
All i love my baby.
になる。さらにパースの述語記号を使い、my baby を j と書くと、これは、
All i lij
と書ける。
ところが、もし、人(persons)にすべて通し番号がついているとすると、 i や j は、0, 1, 2, 3…という数字だと思ってもよい。
もし、my baby の番号が5番だとすると、これは、
All i li5
と書ける。
ところが、これは
l05 かつ l15 かつ l25 かつ l35 かつ l45 かつ l55 かつ l65 …
つまり、ブール代数の記法では、
l05 × l15 × l25 × l35 × l45 × l55 × l65 …
つまり、
l05 l15 l25 l35 l45 l55 l65 …
のことである。
数学では、こういう数列の積を
Πi li5
と書く。これがパースのΠの意味であり、それは、「すべての i に対して、li5 である」を意味している。
同じように、以上の説明の「かつ」、つまり、ブール代数の掛け算を、ブール代数の足し算、つまり、「または」に置き換えると、
l05 または l15 または l25 または l35 または l45 または l55 または l65 …
つまり、ブール代数の記法では、
l05 + l15 + l25 + l35 + l45 + l55 + l65 …
となるが、これは数学の記号を使うと、
∑i li5
になる。これがパースの∑の意味で、それは、「ある i に対して、li5 である」を意味している。 つまり、「誰かが my baby を愛している」「ある人が存在して、その人は my baby を愛している」となる。
以上の説明から、
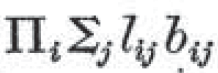
を直接的に日本語に訳してみると、
すべての人 i に対して、ある人 j が存在して、i は j を愛していて、かつ、i は j に施しをする
と読める。つまり、
全ての者は、誰かを愛しており、また、その者に恩をなす
と読める。
そこで、これを使って、「my baby が愛しているのは私だけ」を表現してみよう。
まず、7 が私の番号だとする、そうすると、この文章は、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
となる。
i はXXだ
は、等号を使うと、
i =XX
と書けるし、これは数学風だから、OKとして、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
は、
全ての者(person) i は、my baby がその者 i を愛しているならば、i = 7
となる。(7が「私」の番号!)
「ならば」は、まだブール代数の値で定義していないが、これは伝統的に、
A ならば B = -A または B
と定義することになっている。
そうすると
真ならば真 は 真
真ならば偽 は 偽
偽ならば真 は 真
偽ならば偽 は 真
となる。
この内、3番目以外は納得できるだろうが、3番目を納得するのは難しい。
これを認めると、間違った前提から、どんな命題(主張)でも結論してよいことになる。
これは論理学が常識と大きく隔たる処で、古来、その意味が繰り返し議論されているが、
今でも解決できていない問題である。
以上の「規約」のもとで、but my baby loves only me 7、つまり、
全ての者(person) i は、my baby がその者 i を愛しているならば、実は、 i は私だ!
は、
Πi (-l5i+ (i = 7))
となる。
したがって、先にみた、everybody loves my baby の歌詞の赤で示した部分 を記号論理学でかけば、
Πi li5 Πi (-l5i+ (i = 7))
となる。これを英語風にかけば、
(For any person i. i loves my baby ) and
(For any person i. "my baby loves i" implies "i is me")
となる。
また、any person でなくて、anything にしたければ、次のようにする:
(For anything i." i is a person" implies "i loves my baby") and
(For anything i. "i is a person and my baby loves i " implies "i is me")
パースの論理学や、それに関連した論理学から進歩した現代の論理学の代表は、述語論理学。より正確には第一階述語論理学という。
これを簡単に説明してアリストテレス論理学との相違を説明する。アリストテレス論理学と述語論理学では、同じ用語が違うものを表しているので混乱しないように注意。
アリストテレス論理学の singular term、たとえば、「ソクラテス」に対応するもの.
ただし、terminus (境界、柵)は考えず、その中にある丁度一つの個体を表していると考える。
アリストテレス論理学で、ソクラテスという対象、個体を表す名辞を考えて、
それを So、人間の全体を表す名辞を考えて、それをHu とすると、
「ソクラテスは人間である」が、
So be Hu
と書けた。図にすると
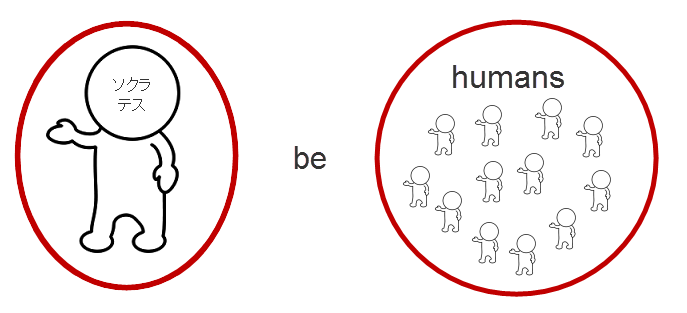
アリストテレス論理学の名辞を数学の集合だと考えれば、
So be Hu
とは、
So ⊆ Hu
のこと、つまり、
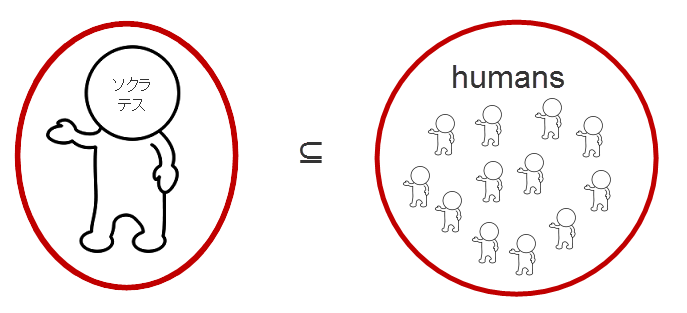
ということ。
述語論理では、これを、ソクラテスの terminus を取り払って、数学の集合論で 9∈{1,3,5,7,9...} とするように、
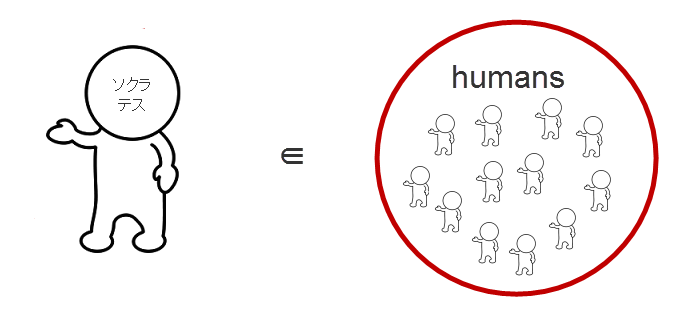
と考える。

ではなくて、柵なしの個

を表す定数記号を so とすると、
So ⊆ Hu
ではなくて、
so ∈ Hu
と考えるということ。
この so を、述語論理学では、term と呼ぶ。
アリストテレス論理学の場合の term は、名辞と和訳されていて、だから、名辞論理学という日本語があるのだが、述語論理学の場合の term は、項と訳される。これは、多項式というような時の、数学の項という用語(英語ではterm)から来ていると思われる。
上の例では、so ∈ Hu と書いたが、述語論理学では、集合の∈は使わないで、述語記号というものを考えて、これを数学の関数のように書く。
具体的にいうと、 Humans という集合にあたる述語記号 Hum を考えて、
so ∈ Hu
を、
Hum(so)
と書く。
この関数の書き方 f(x) に似た書き方が便利なのは、f(x,y) の様な二変数の関数のようなものが使える点。
たとえば、i loves j は、パースでは、
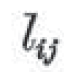
だった。これは2変数の数列のような記号だが、数列というのは、この Wikipedia の数列の記事にあるように、実は関数、
この場合では2変数関数のことだから、Loves という2変数の述語記号を考えて
Loves(i,j)
と書く。これは、下付きの添え字を使わないで済むので、パースの記号より楽。
この様な、多変数の述語を使えるところが、述語論理の優れた点であるが、1変数の述語、たとえば、Hum は、アリストテレス論理学の名辞、つまり、term である Hu に対応している点に注意しなくてはいけない。
一般に、Loves(i,j)のような多変数の述語は、i,j の対、あるいは、タプル [i,j]を考えれば、Lo([i,j])という1変数の述語と見なすことができる。
つまり、Lo とは、「 i loves j であるようなタプル [i,j]」という名辞である。
これを考えると、次のような対応になっていることが分かる
| 伝統論理学 | 名辞 (term) | なし |
| 述語論理学 | 述語 | 項 (term) |
10月24日の資料で名前がでてきた、イギリスの哲学者バートランド・ラッセルは、現代的数理論理学の成立に非常に大きな役割をした人である。
そのラッセルの1903年の著書 The Principles of Mathematics は、後の著作 Principia Mathematica とともに、現代的記号論理学や述語論理学の成立への重要なマイルストーンである。
ラッセルは、この著作では、まだ、term を、伝統論理学、つまり、名辞論理学と同じ意味で使っている。ラッセルが、この著書で、名辞論理学に対して、どういっているかを見てみよう。
ラッセルは、この本で、class と class-concept という言葉で、集合と集合の定義を区別した。クラス class というのは、このころ物の集まりに対して使われていた言葉。現代的に言えば、集合だと思えばよい。
たとえば、先に見た、ケインズの論理学の教科書でも、唯の集まりを表す用語として、class が使われている。
一方で、class-concept というのは、そういうクラスを定義するときに使われる概念という感じ。
たとえば、
{2 4 6 8 10} と {x|x は10以下の偶数}
は同じクラス(集合)だが、右の「x は10以下の偶数」が、class-concept。
つまり、高校で習う、外延的定義と内包的定義の、内包的定義の方で、定義するために使われるものが class-concept だと思えばよい。
伝統的論理学が、ほぼ、現在のような形なったといわれるのは、1662年にフランスのポールロワイヤル修道院で書かれた通称「ポールロワイヤル論理学」という本からである。こちらが英訳。
そのポールロワイヤル論理学には、外延 extension (extent ともいう)、内包 intension という言葉があり(もとの本では、intension ではなく comprehension という用語だが、現代的な用語で書く)、内包は、Termが本来持つべき属性で、それが無くなると、もう、そのTermであらわされるものにならないようなもの、つまり、Termの本質のようなものとされた。一方で、外延は、そのTerm、あるいは、Termの内包が表すもの全部を集めたものとされていた。
たとえば、ポールロワイヤル論理学では、直角三角形という Term の内包には、その外延、図形、三つの辺、三つの角、直角三角形の法則、などが含まれると説明されている。
そして、内包の属性の一つとされた外延とは、そういう内包をすべて所有する、個々の直角三角形の集合のことである。
つまり、いままで、Term を集合として説明してきたが、正確に言うと、これは Term 名辞の外延である。また、ある名辞の外延は、その名辞が本質的に持つものなので、これも内包に含まれるとされる。
名辞論理学では、内包の方が外延より本質的であるとされるが、実は、内包というものは、よくわからないものでもある。それに比べると、外延の方が、すっきりわかりやすい。
この哲学的な内包概念をやめて、最初から、外延で論理を作り直したものが、数学の集合論や記号論理学だともいえる。
しかし、そういう集合としての Term を定義するさいには、やはり、{x|x は10以下の偶数} の赤字の部分のようなものが必要なので、ラッセルは、ここにだけ intension を、残して、これを class-concept と呼んだ。おそらくは、それが継承されて、高校で教えられるような、外延的定義、内包的定義という用語が生まれたと思われる。
ラッセルのThe Principles of Mathematicsでは、名辞としての Term の内包にあたるものは、このように class の「定義」にだけ使われるものに限定されるようになり、class、集合、外延と並置されるようなものではなくなっている。これにより、ラッセルは、内包にまつわる哲学的曖昧を避けることに成功している。
それにも関わらず、この1903年の本では、Term という英語は、まだ、伝統的論理学の名辞の意味として使われ続けており、また、伝統的論理学と、彼の新アプローチの違いが、いろいろと議論されるために、伝統的論理学的な議論が多くみられる。
それをいくつか紹介:
セクション21で、ラッセルは、新しい論理学では、「ソクラテスは人間である」を、So ⊆ Hu ではなくて、so ∈ Hu と理解することを説明した。
古い論理学(名辞論理学)では、A⊆BとA∈Bが同じ categorical propositon として混同されて理解されている。このことを指摘したのが、イタリアのペアノで、この指摘が大変重要である、とラッセルは主張した。」
セクション43では、もともと、命題の基本である categorical proposiotn を subject, copula, predicate で考えたのがおかしい。 動詞を無視している、とラッセルは主張し、
"Socrates is a man" は、 Socrates | is | a man ではなく、 Socrates | is a man と分割すべきで、is a man という一塊が、述語という存在になるのだ、とした。
第4章では、伝統的論理学の名辞についての詳しい議論が行われている。その Chap.IV の題名は、Chap. IV: Proper names, adjectives and verbs.
記号論理学では、こういう日常言語の文法について議論は行われない。これは、1903年の時点のラッセルの記号論理学が、まだまだ名辞論理学とのつながりを残していることを示している。
その4章のセクション46の内容は、目次では、§46. Proper names, adjectives and verbs distinguished と説明されている(この本は、古い形式で書かれていて、本文中の各セクションには、題名がない。
そして、目次 TABLE OF CONTENTS のセクションのリストには、現代ならば、セクションの題名に対応するものが書かれている。
だから、ラッセルがセクション46で主張したことは、固有名詞 proper name, 形容詞 adjective、そして、動詞 verb が区別されなくてはいけない、ということ。
名辞論理学では、これらが、すべて同じ名辞 Term だった。形容詞については、説明していないが、「赤いもの」という名辞が red という形容詞に対応すると考えて、The apple is red. という文を categorical proposition であるとするということ。
また、セクション47は、目次では、Terms という題名がついていて、ここで、 Whatever may be an object of thought, or may occur in any true or false proposition, or can be counted as one, I call a term. This, then, is the widest word in the philosophical vocabulary. と、Term を説明している。これは、名辞論理学の term と本質的に変わりがない。
しかし、ラッセルは、セクション48で、その Term には、実は二種類あるとする。次が原文
Among terms, it is possible to distinguish two kinds, which I shall call respectively things and concepts.
The former are the terms indicated by proper names, the latter those indicated by all other words.
つまり、ここで、はっきりと、ソクラテスのような固有名詞が表す Term と、人間の様な一般名詞が表す Term を区別し、前者を thing 物、後者を concept と呼ぶ。
そして、後の述語論理学では、この thing を表すものが term と呼ばれるようになり、concept は、述語 predicate と呼ばれるようになったわけである。