論理学の歴史資料

論理学の歴史資料　2016.10.31

資料用ＩＤとパスワード

尾崎咢堂の論理学の教科書はコピーライドが消失しており、ＷＥＢで公開されていますが、これからコピーライトがあるもの、どうだか良くわからないものを幾つか使います。

ＰＤＦで配布しますが、コピーライトがあるので、パスワードによるアクセス制限をかけます。

今回の授業の最初に、そのパスワードとＩＤを見せますので、書き留めてください。(ただし、今回分は、全部パスワードなしで大丈夫のはず。）

前回の資料から

以上を踏まえて、ここから尾崎行雄著、演繹推理学（国会図書館デジタルコレクションへのリンク）、明治15年刊を使って、アリストテレス論理学入門

疑問：なんでそんな古い本？

日本語で良い本を探してみたが見つからなかった。驚くことに、この古い本が一番手短に良くまとまっていた。また、これだとオリジナル（の画像）が無料で見られる。
- だらだらと長いものならばあるが、この講義は論理学を学ぶことが目的ではないので。
これが明治の大論理学ブームを象徴するものだから。（こちらの理由の方が大きい）
- 後で、この大論理学ブームについてみて、平成の小論理学ブームと比較する。
- 尾崎は政治家として大変に有名な人。憲政の神様と呼ばれ、国会前に銅像が立っている。
- なぜ、その人が論理学の教科書を書いたのか？これが最大のポイント！
  - 詳しい所は、その時、この本の序を使って説明する。
  - しかし、序の出だしだけ見ておく：
    - 演繹推理学序(現代語訳:不適切な言葉が使われていますが、原作を尊重して訳してあります。（＾＾；））
      - 思想あれば茲に（げんに）言語あり。苟も（いやしくも）人たる以上は如何なる蛮野未開の民と雖も（いえども）、多少の思想なくんばあらず故に、之を発露するの言語あるなり。
      - 文運の未だ普及せざる尚お文字文章を知らざるの民あり。言語なきの人民あらず。
      - 唯だ言語は思想に伴うて進退消長す。蛮民も思想や粗雑にして僅少なり故、其言語も亦粗雑にして僅少なり。
      - 開明人の思想や精緻にして多し故に、其言語も亦精細にして多し。
      - ……

名辞概論

尾崎の演繹推理学第三章のタイトルが名辞概論．

この名辞という概念が、もっとも重要なポイント。

名辞のＷＥＢ上の説明を幾つか：１、２

名辞は英語では term。だから、これが重要となる論理なので、アリストテレス論理学のことを Term logic ともいう。

記号論理学も、西田の論理（哲学）も、名辞から述語に重点を移動させた。

ちなみに、評論家の松岡正剛さんという人が、西田の論理が、フレーゲの記号論理学を先取りしたかのように書いているが、フレーゲの記号論理学の方が西田の論理より半世紀近く古い：　Frege 1879, Russell でさえ 1903。西田の「場所」が1926年、「述語的論理主義」が1928年。（西田著作年表）
- また、松岡さんの議論には、哲学的にも問題が多いので、信じないように。
ちなみに、現代的な第一階述語論理が初めて形を現したのは1928年（Hilbert, Ackermann)。
これと名前が似ているので、この講義でも、西田の「述語的論理主義」と述語論理に何か関係があるよう考える人を時々みかけるが、この二つは、どちらも名辞から述語に重点を移したという以外は、まったくの別物なので注意。
- 西田の場合では、「重点を述語に移した」のではなくて、「重点を述語面に重点を移した」という方が正確。
記号論理学的な「述語への移行」の意味は、後で Russell の 1903 年の著書の分析のところで説明する。
これらの二つの「重点移動」が何だったかを理解するには、移動する前の名辞の論理学としての伝統的論理学の理解が不可欠。
この名辞論理学が忘れられているので、西田の述語的論理主義（場所の論理）と、述語論理の confusion　が起きる。
この講義の内容を理解して、それから、上の松岡さんの議論を読むと、それがよくわかるはず。

つまり、これらの論理が乗り越えようとしたのは、この名辞という概念なのである。

そして、その名辞とは、この動画で言われている東洋人と西洋人のものの見方の違で、西洋的とされている境界がハッキリとしている「物」「対象物」のことだと思えば良い。

哲学的に言うと、ちょっと違っていて、実は名辞が何かには、哲学者により歴史上様々な異なる意見が出されている。しかし、ここでは、そういう難しいことは考えない！
また、ここでの「対象物」には、「人という概念」などの「概念」も含まれる。というより、そちらの方が名辞としては普通。
また、この動画は、娯楽番組の記録ですが、心理学専修の先生方にお聞きしたところ、虎の絵への視線の話など、よく知られた実験結果だそうで、まっとうな心理学の成果だそうです。
- また、子供は、東洋的と、この動画で呼ばれている傾向を示すとも教えてもらいました。これも面白いですね。：

ここから尾崎の名辞論の解説を見ていく

尾崎の教科書の10-11頁に次のような名辞の例が書かれている：

論語，猛子，英国王
馬，国王，府県会

尾崎は，１のような名辞を「唯一個の人あるいは一個の事物を指言する者」と説明し，２のような名辞を「諸種の馬，諸国の王，諸方の府県会を指言する者」と説明し，それぞれ，

特称名辞
通称名辞

と名づけている．

たとえば、孟子は特称名辞。また、人、中国人、学者は通称名辞。

命題概論

命題というのは意味を持つ文章のことだと思っておけばよい。

アリストテレス論理学では、命題の基本単位は、二つの名辞から作られる

A be B

という形であると考える。ここで、Ａ　と B が名辞。

たとえば、次のものはみなそういう形をしている。

孟子　is 　人

孟子　is 　中国人

孟子　is 　学者

中国人 are 人

学者 are 人

以上は皆正しいもの。

しかし、

中国人 are 孟子

人 are 学者

は間違い。

Categorical proposition

尾崎は A be B のような形の基本形の命題を合式命題と呼んでいるが、これは普通の用語では、categorical proposition と呼ばれている。（日本語訳がわからない。ない？）

その定義は、尾崎の説明の通りで、二つの名辞をコピュラ、copula、繋辞（けいじ）、連辞（れんじ）で結んだもの。

A be B のＡを主語、Ｂを賓語（ひんご、今の普通の日本語でいえば目的語）という。

何か変。賓語は漢文（中国語）の文法用語ではないのか…？？？

実は、アリストテレス論理学は、英語やドイツ語、ラテン語などの言語の構造に根ざしている所があり、例えば、英語を使うと説明しやすいが、日本語に例えて説明すると不自然になる！

そこで、日本語の対応する用語を使う尾崎の解説を使うのは、ここまでにして、

以下では、経済学者　John Maynard Keynes　の父である John　Neville Keynes の論理学の教科書を使って、これを日本語に引き当てず、英語に引き当てて、説明していく。

これが Keynes の教科書、Studies and Exercises in Formal Logic　の第2版の、該当部分。

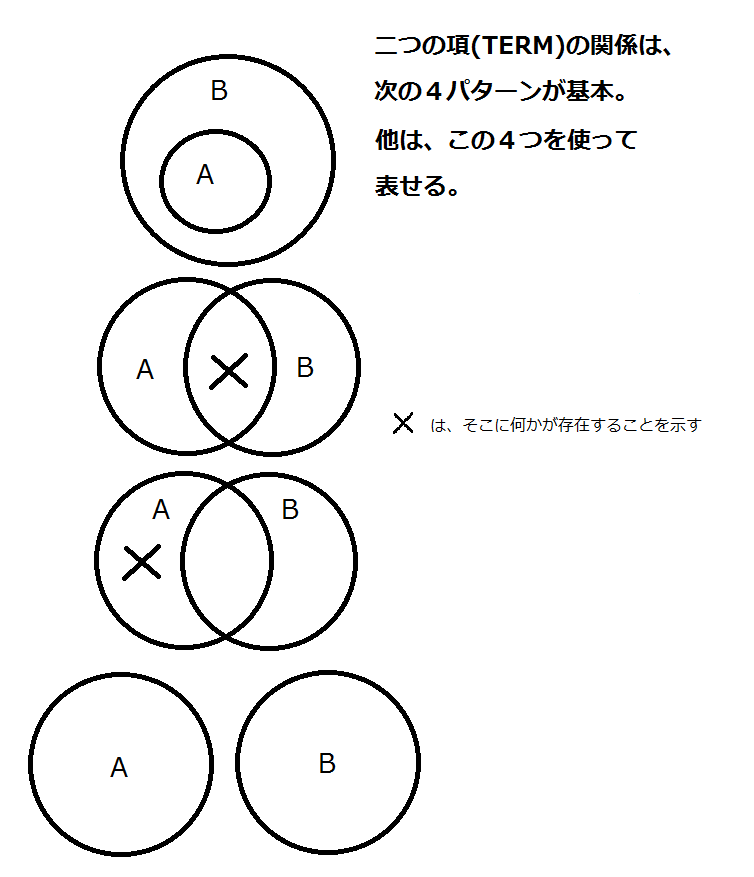
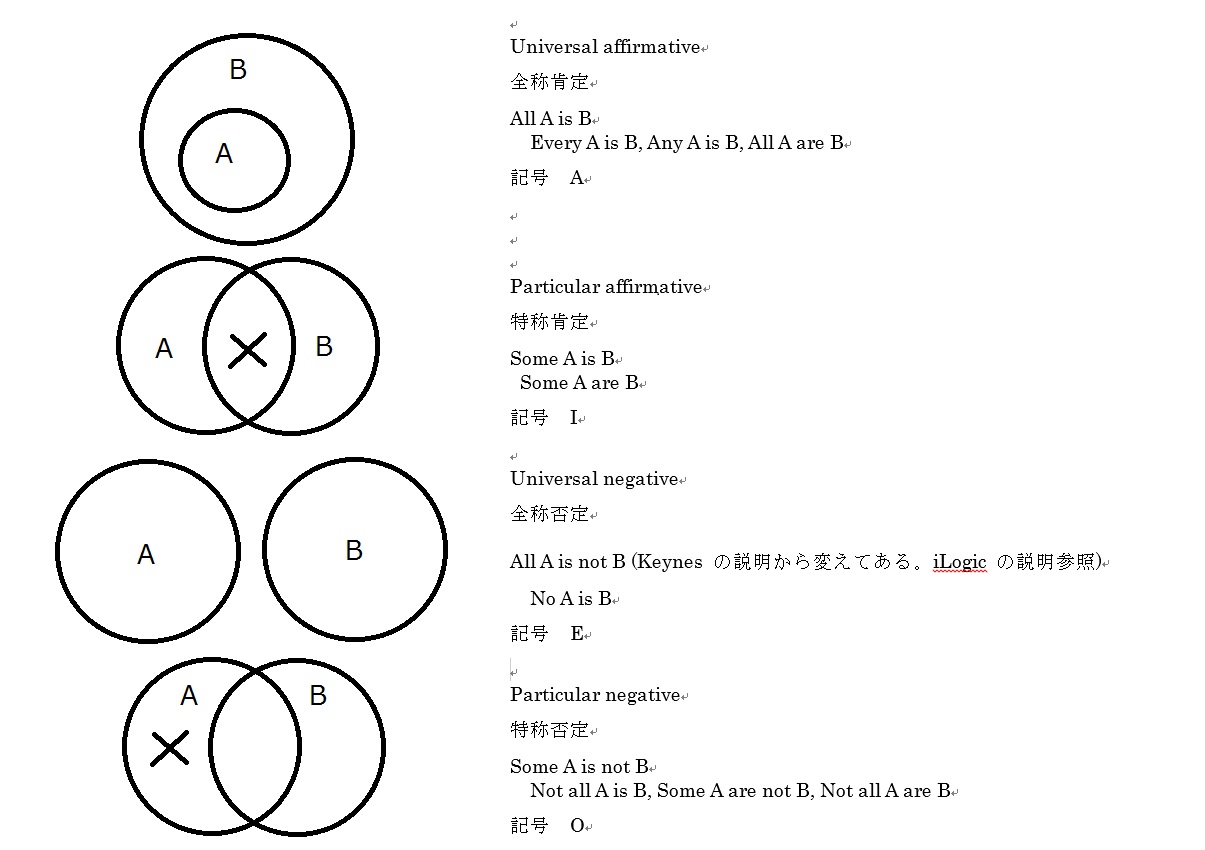
基本的には、二つの名辞の関係性には、名辞を集合だと思うと、対称的なものを同一視すると、次の4パターンしかないことがわかる。

他にもありそうな気が…

しかし、良く考えてみると、二つの項の関係は、本質的にはこの4パターンに還元できることがわかる。

たとえば、

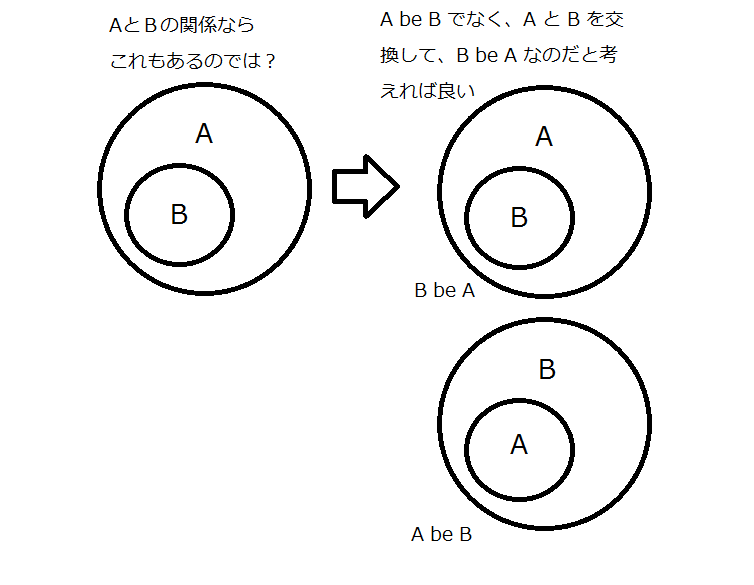
さらに…

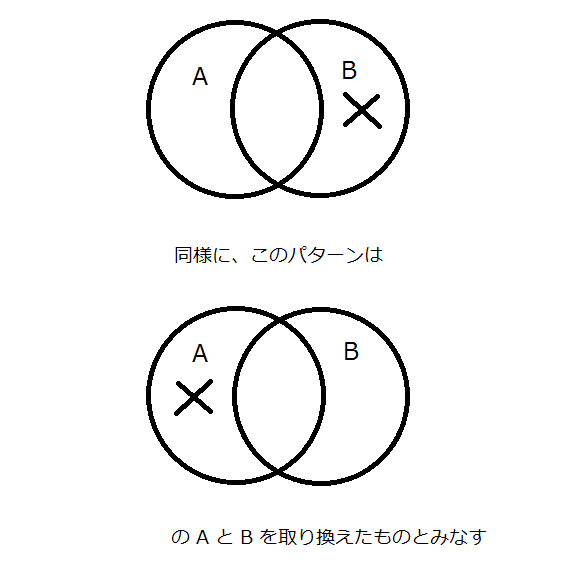
もうひとつ…

４パターンに対応する Categorical Porpositions の名称

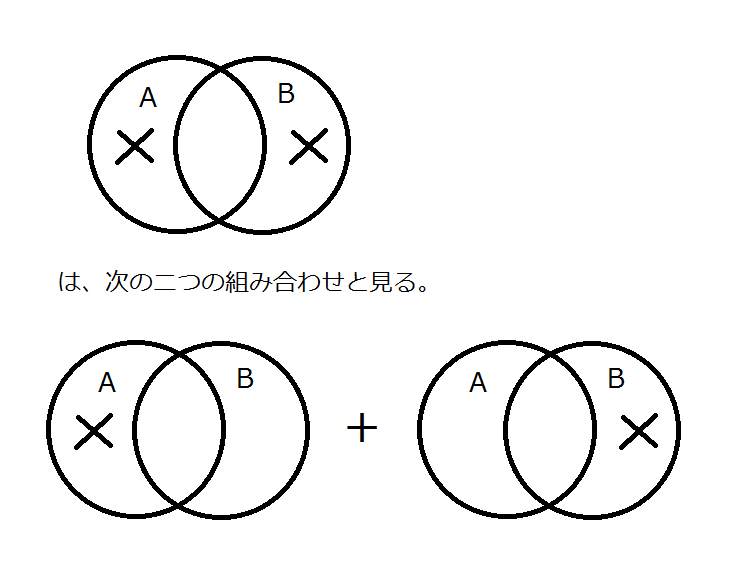
Keynes の教科書を参照すること

上の話の参考資料

Butte Colledge の iLogic での説明　アメリカのコミュニティカレッジ（らしい）の論理学の資料。よくできていて、直感的にわかる。

推論の形式の学としての Syllogism （三段論法）

ここから三段論法の話。ここでアリストテレス論理学の名辞論に潜む不思議な話が明らかになる。そして、それは前回のテレビ番組の西洋的世界観と奇妙に一致する。

その話をする準備として、まずは、ビデオにも出てきたが、虎の絵から…

英語で「三匹の虎」は

Three Tigers

同じく、２匹。

Two Tigers

そして、一匹の虎。

A Tiger

three tigers, two tiger, a tiger は、いずれも term.　前二者は複数形、最後のだけ単数形であることに注意。

日本語には、こういう区別がないが…

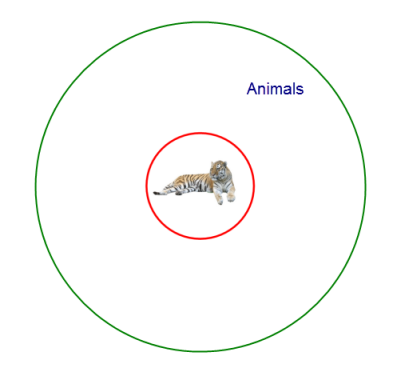
Butte college iLogic の恐竜 dinaosors という名辞が記述(denotes)するものは恐竜の集合と説明されていた。

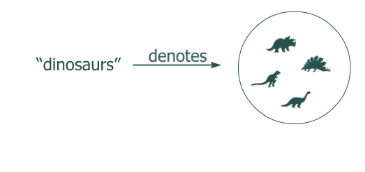
これに従って、上の三つのケースを考えると、

Set of Three Tigers

Set of Two Tigers

Set of A Tiger

ということになる。

つまり、a tiger も集合！

固有名辞としての the tiger

柵、境界、分離するもの、分別するものとしての term

上の図で、the tiger が、他の二匹の虎と分離されていることに注意。

ビデオで見た、外界、環境、周囲から、個物を分離して考えるという思考法に一致している。

実際、term の語源は、柵、境界などを意味するラテン語の terminus から来ていて、プラトン、アリストテレスの時代には、言語がギリシャ語で境界、極限を意味する horos という単語で呼ばれていた。

参考　ブリタニカの説明

集合としてのソクラテス

論理と言えば、有名な三段論法

ソクラテスは人間である。
人間は死ぬものである。
ソクラテスは死ぬものである。

がある。人間、死ぬもの、はどちらも名辞であり、２の「人間は死ぬものである」は、典型的なＡ型の命題、つまり、全称肯定命題。

では、１の「ソクラテスは人間である」と「ソクラテスは死ぬものである」は？

文章の形から、あきらかに、Ａ be B の、A という主語の名辞は、「ソクラテス」！

実は、この様な、場合も名辞「ソクラテス」を集合と考える。

つまり、

この図は、本当は変なので、説明のための方便と考えてください。
何が変なのかは、右の terminus の中のソクラテスを、terminus つぎのソクラテスに置き換えればわかります。（無限後退）

どうしてこの様に考えるのか

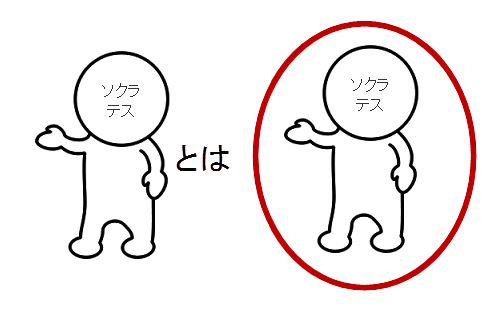
実はこの様に考えると、英語の

A is a B, A is the B

の様な文章と

A are B

が同じ種類の文章、あるいは、命題として考えることができる。

たとえば、

The three tigers are animals.

The tiger is an animal.

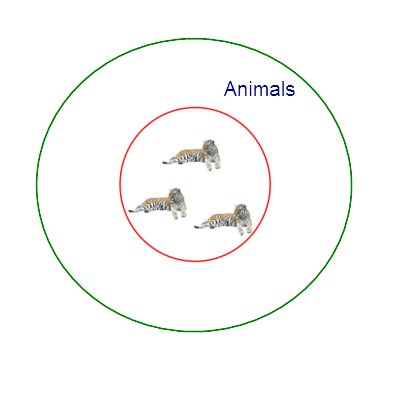
この様に考えると、上の三段論法

ソクラテスは人間である。
人間は死ぬものである。
ソクラテスは死ぬものである。

の三つの文章がすべて概念的に同じ構造、つまり、二つの term を連辞で繋いだ

Ａ　ｂｅ　Ｂ

の形、しかも、すべてがＡ型の全称肯定命題であることがわかる。

つまり、

ソクラテスは人間である。

の本当の意味は、

すべてのソクラテスは人間である。

ということになる！

不自然なようにも感じるが、

恐竜は動物だ。

という命題も、恐竜が絶滅寸前で、恐竜が最後の一ぴきしかいない状況では、「ソクラテスは人間である」と同じ様な状況であることに注意。

シロギズム　推論の理論

先ほどの三段論法の前提、つまり、1－3の内の、１と２

ソクラテスは人間である。
人間は死ぬものである。

の状況を、今までのようなベン図で重ねて図示してみると

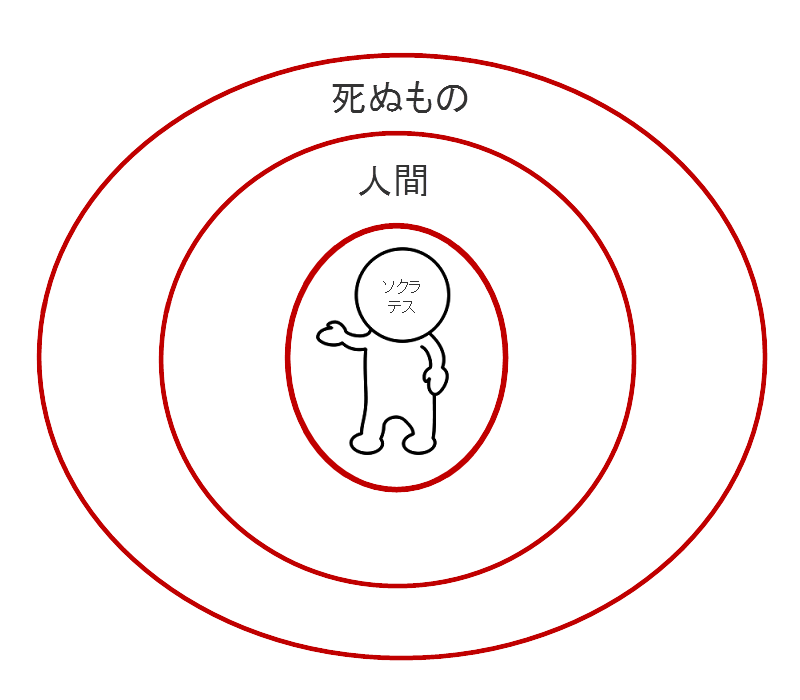
となる。あきらかに、

ソクラテスは死ぬものである。

が分かる。つまり、有名な「ソクラテスは死ぬ」という三段論法は、数学でいう

部分集合の部分集合は部分集合

つまり、

Ａ⊆ＢかつＢ⊆ＣならばＡ⊆Ｃ

のことである。

これは

A be B
B be C

がどちらも全称肯定命題として理解されたとき、 A be B B be C の、中間の B をとって作った A be C という全称肯命題は、二つの前提が正しいときには正しいことを意味している。

同様のことを、１，２　と A be C のそれぞれを、全称肯定、全称否定、特称肯定、特称否定のすべてのパターンで考えて、その推論が正しいかどうかを、ひとつひとつ検討したもの。

それがシロギズムの理論（三段論法の理論）。

図を見ただけでわかると思うが、兎に角、ややこしい…

また、Keynes の教科書にもあるように、実は、「ソクラテスは人である」という命題は、「ソクラテスという人がいる」という特称肯定命題と考えることもできるので、論理学者の間で議論があったらしい。

この様に、名辞を集合と見る立場は、例えば、データベースでの検索などを考えると、割と自然なのだが、理論的、数学的に、話を整理しようとすると混乱が生じることが経験的に分かっている。

で、その欠点を、「述語」の概念を取り入れることにより、解決したのが、数理論理学、記号論理学の体系である述語論理学。

次回からは、その話。